3.4乘法公式（1）课件

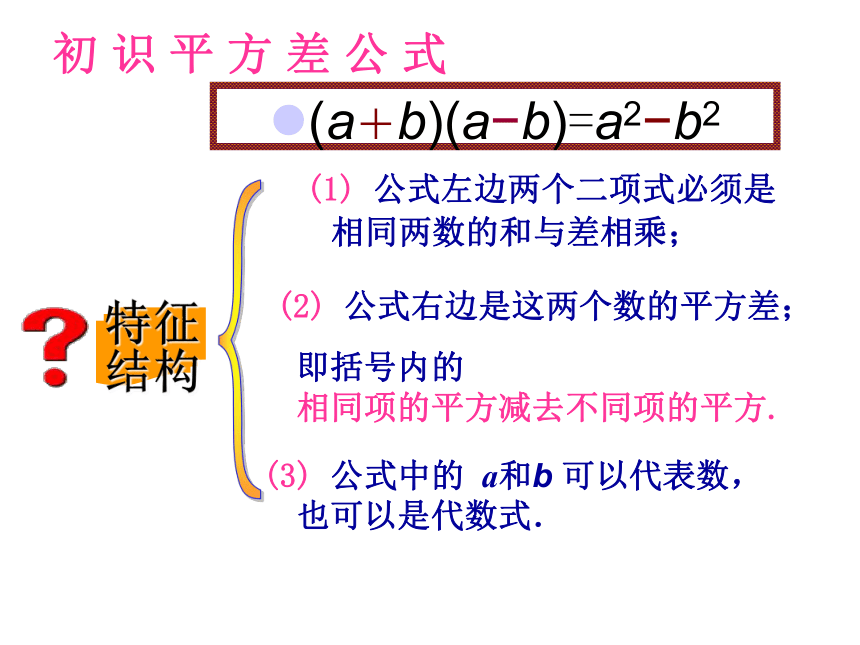
课件13张PPT。§3.4　乘法公式(1)计算下列各题:(1) (x+5)(x?5) ；(2) (3+a)(3?a) (3)(2m+n)(2m?n) ；=x2?25 =9?a2 =4m2?n2 ;=x2?52 ;=32?a2 ;=(2m)2?n2 等号左边前后的两个多项式,它们第一项与第一项，第二项与第二项有什么特点?等号右边与左边什么联系?它是左边两项作什么运算？初 识 平 方 差 公 式(a+b)(a?b)=a2?b2 (1) 公式左边两个二项式必须是相同两数的和与差相乘； (2) 公式右边是这两个数的平方差； 即括号内的
相同项的平方减去不同项的平方. (3) 公式中的 a和b 可以代表数，
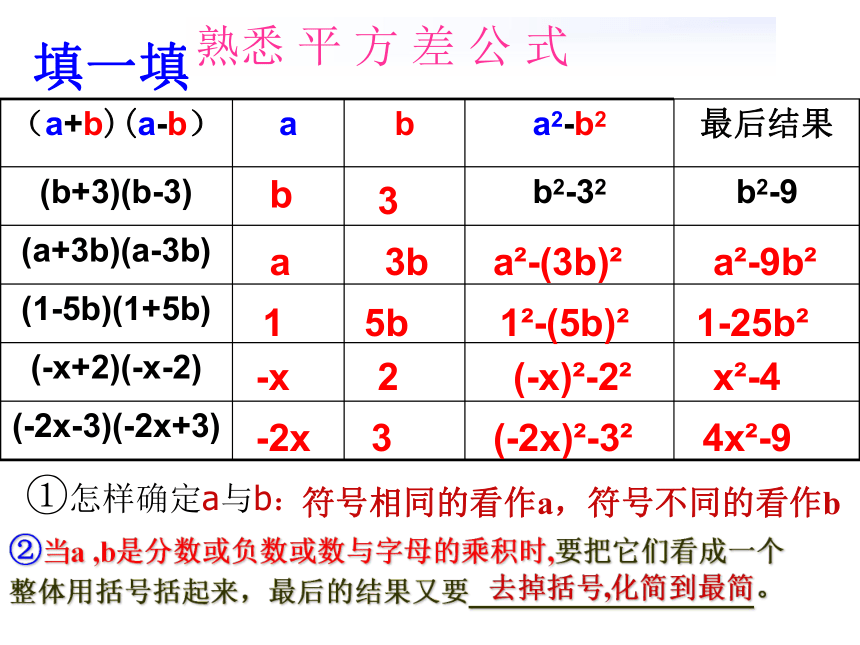
也可以是代数式． b3aa2-(3b)215b12-(5b)21-25b2-x2(-x)2-22x2-4-2x3(-2x)2-32a2-9b24x2-93b填一填①怎样确定a与b：符号相同的看作a，符号不同的看作b
熟悉 平 方 差 公 式②当a ,b是分数或负数或数与字母的乘积时,要把它们看成一个整体用括号括起来，最后的结果又要_________________去掉括号,化简到最简。1.辩一辩：判断并改错：
(1) (a+3)(a-3)=a2-3 ( )
改正：
(2)(5y+2)(5y-2)=5y2-4 ( )
改正：
(3) (-m+7)(7+m)=m2-49 ( )
改正：×××(a+3)(a-3)=a2-9(5y+2)(5y-2)=25y2-4(-m+7)(7+m)=(7-m)(7+m)=49-检验成果:m2 2.下列式子可用平方差公式计算吗? 为什么? 能能 不能 不能(1) (-4k+3)(-4k-3) (2) (1-x)(-x-1)
(3) (-x-1)(x+1) (4)(x+3)(x-2)（ ） 例1 计算：(?4a3?1)(4a3?1)初步尝试:(1) (3x+5y)(3x-5y) 步骤：1、判断；2、调整；3、用公式。
找出相等的“项”和符号相反的“项”，然后应用公式． (4) (-2x+y)(2x-y)(2) ( a+b ) (- a+ b ) (2) ( )(-y-1)=1-y2(1) (-3a2+2b2)( )=9a4-4b4仔细填一填王敏捷同学去商店买了单价是9.8元/千克的糖果10.2千克，
售货员刚拿起计算器，王敏捷就说出应99.96元，结果与售货员计算出的结果相吻合。
售货员很惊讶地说：“你好象是个神童，怎么算得这么快？”
王敏捷同学说：“过奖了，我利用了在数学上刚学过的一个公式。”
你知道王敏捷同学用的是一个什么样的公式吗？怎么计算的吗?解决实际问题例2.利用平方差公式计算:
103×97 (a+b-c)(a-b-c)能用平方差公式运算吗?若能结果是哪两数的平方差?本节课你的收获是什么？小结本节课你学到了什么?1、会用语言表述平方差公式 (a+b)(a?b)=a2?b2。2、应用平方差公式 时要注意一些什么？两数和与这两数差的积，等于它们的平方差。变成公式标准形式后，再用公式。 或提取两“?”号中的“?”号，运用平方差公式时，要紧扣公式的特征，
找出相等的“项”和符号相反的“项”，然后应用公式； 要利用加法交换律，对于不符合平方差公式标准形式者，