2.3.2 加减消元法-解二元一次方程组 课件
文档属性
| 名称 | 2.3.2 加减消元法-解二元一次方程组 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-09 19:41:23 | ||
图片预览






文档简介
课件26张PPT。第二章 二元一次方程组2.3 解二元一次方程组2.3.2 加减消元法课时导入今有鸡兔同笼
上有三十五头
下有九十四足
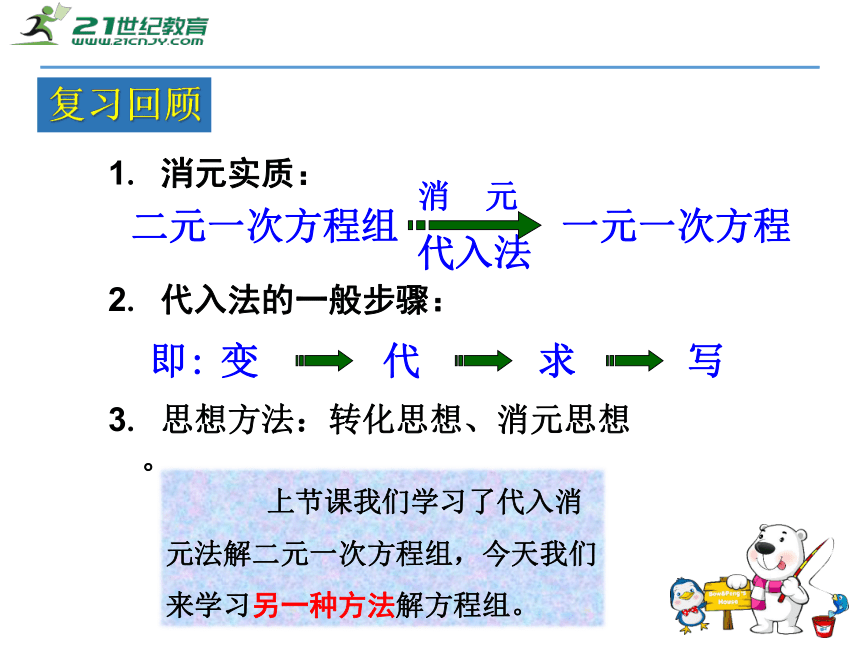
问鸡兔各几何解:设鸡有x只,兔有y只,由题可列出方程组:中国古算题:鸡兔同笼1. 用上节课的方法解该方程组2. 还有其他方法解该方程组吗?复习回顾1. 消元实质:2. 代入法的一般步骤:3. 思想方法:转化思想、消元思想。 上节课我们学习了代入消元法解二元一次方程组,今天我们来学习另一种方法解方程组。观察方程组
它的系数有什么特点?你会用什么方法来消元?
完成这个方程组的求解过程(填空).合作探究解 将方程①②的左右两边分别相加,得______
(依据:________)
解得x=________. 把解得的x的值代入①,得
______,
解得y=________.
所以原方程组的解是_____________.
把上述过程中“①+②”改为“①-②”,结
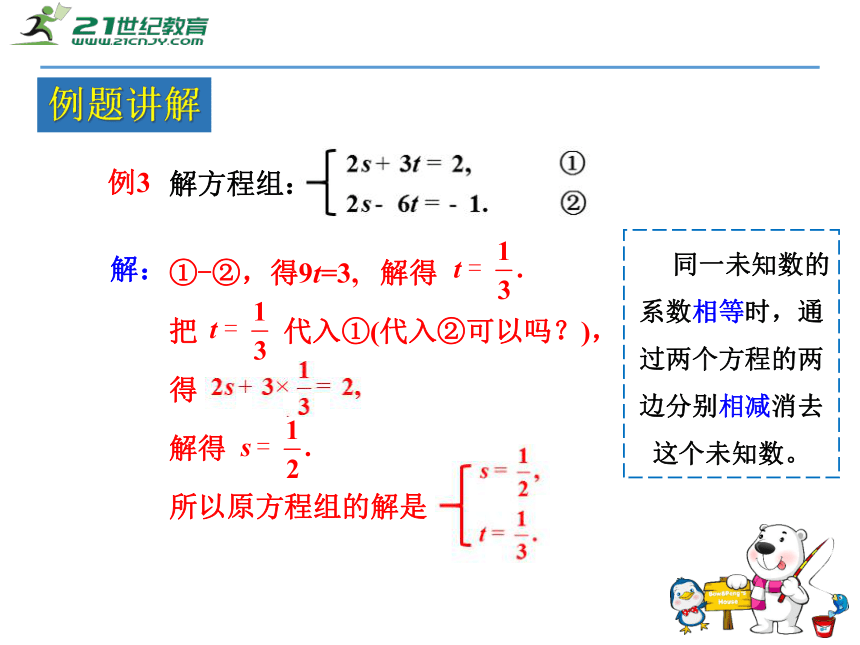
果将如何? 对于二元一次方程组,当两个方程的同一个未知数的系数是互为相反数或相同时,可以通过把两个方程的两边相加或相减来消元,转化为一元一 次方程求解. 这种解二元一次方程组的方法叫做加减消元法,简称加减法. 加减法也是解二元一次方程组常用的方法之一.总结归纳解方程组:
例3解:
①-②,得9t=3, 解得
把 代入①(代入②可以吗?),
得
解得
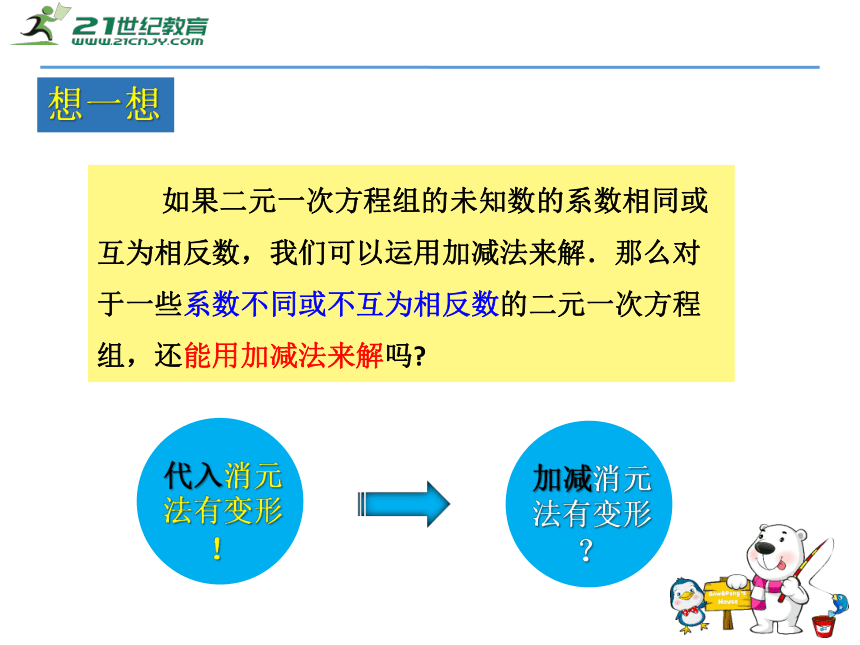
所以原方程组的解是例题讲解 同一未知数的系数相等时,通过两个方程的两边分别相减消去这个未知数。 如果二元一次方程组的未知数的系数相同或
互为相反数,我们可以运用加减法来解.那么对
于一些系数不同或不互为相反数的二元一次方程
组,还能用加减法来解吗?想一想代入消元法有变形!加减消元法有变形?解方程组:
例4
先通过方程的变形,使得某个未知数的系数的绝
对值相同, 就可以把两个方程的两边相加或相减
来消元.分析:例题讲解试一试解:
①×3,得9x-6y=33. ③
②×2,得4x+6y=32. ④
③+④,得13x=65,
∴ x=5.
把x=5代入①,得 3×5-2y=11,
解得 y=2.
所以原方程组的解是例题讲解用加减法解二元一次方程组的一般步骤是:
1.将其中一个未知数的系数化成相同(或互为相反数).
2.通过相减(或相加)消去这个未知数,得到一个一元
一次方程.
3.解这个一元一次方程,得到一个未知数的值.
4.将求得的未知数的值代入原方程组中的任一个方程,
求得另一个 未知数的值.
5.写出方程组的解.总结归纳拓展训练 1 解方程组:
导引:方程①和②中x,y的系数的绝对值都不相等,
也不成倍数关系,应取系数的绝对值的最小
公倍数6,可以先消去x,也可以先消去y.做一做:用消x或消y的方法解:方法一:①×3,得6x+9y=9.③
②×2,得6x+4y=22.④
③-④,得5y=-13,即
把
解得
所以这个方程组的解为代入①,拓展训练方法二:①×2,得4x+6y=6.⑤
②×3,得9x+6y=33.⑥
⑥-⑤,得5x=27,解得
把
解得
所以这个方程组的解为代入①,拓展训练 用加减消元法解二元一次方程组时,一般有三种情况:
①方程组中某个未知数的系数的绝对值相等,则直接利用加减法求解;
②方程组中任一个未知数的系数的绝对值都不相等,但某个未知数的系数的绝对值成倍数关系,则其中 一个方程乘这个倍数后再利用加减法求解;总结归纳③方程组中任一个未知数的系数的绝对值既不相等,
也不成倍数关系,可利用最小公倍数的知识,把两
个方程都适当地乘一个数,使某个未知数的系数的
绝对值相等,然后再利用加减法求解.拓展应用解较复杂的二元一次方程组解方程组:1 将方程组化简成一般形式,用代入法或加减
法解方程组.导引:方法一:将原方程组化简,得
由①,得y=36-5x. ③
把③代入②,得-x+5(36-5x)=24,解得x=6.
把x=6代入③,得y=36-5×6=6.
所以原方程组的解是解:方法二:将原方程组化简,得
①×5,得25x+5y=180. ③
③-②,得26x=156,解得x=6.
把x=6代入①,得y=6.
所以原方程组的解是拓展应用总结:当化简后的方程组存在一个方程的某个未知数系数的绝对值是1或有一个方程的常数项是0时,用代入法;当两个方程中的某一个未知数系数的绝对值相等或成倍数关系时,用加减法.解特殊的二元一次方程组拓展应用2解方程组:通过观察两个方程都有2x-3y,于是考虑整体
代入②即可.导引:由①得2x-3y=2,③
把③代入②,得 +2y=9.
解得y=4. 把y=4代入①得2x-3×4-2=0,
解得x=7.
故原方程组的解是解:利用整体代入法解二元一次方程组解方程组:方程组中x的系数分别为13,14,y的系数分别为
14,13. 当两式相加时,x和y的系数相等,化简
即可得到x+y=a;当两式相减时,x和y的系数
互为相反数,化简即可得到x-y=b. 由此达到
化简方程组的目的.导引:做一做①+②,得27x+27y=81.化简,得x+y=3.③
①-②,得-x+y=-1.④
③+④,得2y=2,y=1.
③-④,得2x=4,x=2.
所以这个方程组的解是解:做一做 形如 的方程组,其求解过程可以总结为四步:
第一步,①+②,得到x+y=m③的形式;
第二步,①-②,得到x-y=n④的形式;
第三步,③+④;
第四步,③-④.
或者
第一步,①+②得到x+y=m③;
第二步,由③得x=m-y或y=m-x④;
第三步,将④代入方程②或①求解即可.总结归纳1 (中考·河北)利用加减消元法解方程组
下列做法正确的是( )
A.要消去y,可以将①×5+②×2
B.要消去x,可以将①×3+②×(-5)
C.要消去y,可以将①×5+②×3
D.要消去x,可以将①×(-5)+②×2
中考链接用加减法解方程组.
(1)(中考·东营)
(2)(中考·荆州) 2中考链接3 解方程组:
(1)(中考·无锡)
用整体代入法解方程组1用换元法解方程组:2课堂练习加减消元法的定义:
当二元一次方程组的两个方程中同一未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称加减法.课堂小结解方程组时,要根据方程组的特点,选择合适的解法:
(1)当方程组中存在一个方程的某一个未知数系数的绝对值是1或有一个方程的常数项是0时,一般用代入法;
(2)当两个方程中某一个未知数系数的绝对值相等或成整数倍关系时,一般用加减法.用加减消元法解二元一次方程组的一般步骤: (1)变形:将方程组中某一未知数的系数变为相等或
相反.
(2)加减:消去一个未知数.
(3)求解:得到一个未知数的值.
(4)回代:求另一个未知数的值.
(5)写出解.课堂小结完成教材P43作业题T1-T5课后作业谢 谢
上有三十五头
下有九十四足
问鸡兔各几何解:设鸡有x只,兔有y只,由题可列出方程组:中国古算题:鸡兔同笼1. 用上节课的方法解该方程组2. 还有其他方法解该方程组吗?复习回顾1. 消元实质:2. 代入法的一般步骤:3. 思想方法:转化思想、消元思想。 上节课我们学习了代入消元法解二元一次方程组,今天我们来学习另一种方法解方程组。观察方程组
它的系数有什么特点?你会用什么方法来消元?
完成这个方程组的求解过程(填空).合作探究解 将方程①②的左右两边分别相加,得______
(依据:________)
解得x=________. 把解得的x的值代入①,得
______,
解得y=________.
所以原方程组的解是_____________.
把上述过程中“①+②”改为“①-②”,结
果将如何? 对于二元一次方程组,当两个方程的同一个未知数的系数是互为相反数或相同时,可以通过把两个方程的两边相加或相减来消元,转化为一元一 次方程求解. 这种解二元一次方程组的方法叫做加减消元法,简称加减法. 加减法也是解二元一次方程组常用的方法之一.总结归纳解方程组:
例3解:
①-②,得9t=3, 解得
把 代入①(代入②可以吗?),
得
解得
所以原方程组的解是例题讲解 同一未知数的系数相等时,通过两个方程的两边分别相减消去这个未知数。 如果二元一次方程组的未知数的系数相同或
互为相反数,我们可以运用加减法来解.那么对
于一些系数不同或不互为相反数的二元一次方程
组,还能用加减法来解吗?想一想代入消元法有变形!加减消元法有变形?解方程组:
例4
先通过方程的变形,使得某个未知数的系数的绝
对值相同, 就可以把两个方程的两边相加或相减
来消元.分析:例题讲解试一试解:
①×3,得9x-6y=33. ③
②×2,得4x+6y=32. ④
③+④,得13x=65,
∴ x=5.
把x=5代入①,得 3×5-2y=11,
解得 y=2.
所以原方程组的解是例题讲解用加减法解二元一次方程组的一般步骤是:
1.将其中一个未知数的系数化成相同(或互为相反数).
2.通过相减(或相加)消去这个未知数,得到一个一元
一次方程.
3.解这个一元一次方程,得到一个未知数的值.
4.将求得的未知数的值代入原方程组中的任一个方程,
求得另一个 未知数的值.
5.写出方程组的解.总结归纳拓展训练 1 解方程组:
导引:方程①和②中x,y的系数的绝对值都不相等,
也不成倍数关系,应取系数的绝对值的最小
公倍数6,可以先消去x,也可以先消去y.做一做:用消x或消y的方法解:方法一:①×3,得6x+9y=9.③
②×2,得6x+4y=22.④
③-④,得5y=-13,即
把
解得
所以这个方程组的解为代入①,拓展训练方法二:①×2,得4x+6y=6.⑤
②×3,得9x+6y=33.⑥
⑥-⑤,得5x=27,解得
把
解得
所以这个方程组的解为代入①,拓展训练 用加减消元法解二元一次方程组时,一般有三种情况:
①方程组中某个未知数的系数的绝对值相等,则直接利用加减法求解;
②方程组中任一个未知数的系数的绝对值都不相等,但某个未知数的系数的绝对值成倍数关系,则其中 一个方程乘这个倍数后再利用加减法求解;总结归纳③方程组中任一个未知数的系数的绝对值既不相等,
也不成倍数关系,可利用最小公倍数的知识,把两
个方程都适当地乘一个数,使某个未知数的系数的
绝对值相等,然后再利用加减法求解.拓展应用解较复杂的二元一次方程组解方程组:1 将方程组化简成一般形式,用代入法或加减
法解方程组.导引:方法一:将原方程组化简,得
由①,得y=36-5x. ③
把③代入②,得-x+5(36-5x)=24,解得x=6.
把x=6代入③,得y=36-5×6=6.
所以原方程组的解是解:方法二:将原方程组化简,得
①×5,得25x+5y=180. ③
③-②,得26x=156,解得x=6.
把x=6代入①,得y=6.
所以原方程组的解是拓展应用总结:当化简后的方程组存在一个方程的某个未知数系数的绝对值是1或有一个方程的常数项是0时,用代入法;当两个方程中的某一个未知数系数的绝对值相等或成倍数关系时,用加减法.解特殊的二元一次方程组拓展应用2解方程组:通过观察两个方程都有2x-3y,于是考虑整体
代入②即可.导引:由①得2x-3y=2,③
把③代入②,得 +2y=9.
解得y=4. 把y=4代入①得2x-3×4-2=0,
解得x=7.
故原方程组的解是解:利用整体代入法解二元一次方程组解方程组:方程组中x的系数分别为13,14,y的系数分别为
14,13. 当两式相加时,x和y的系数相等,化简
即可得到x+y=a;当两式相减时,x和y的系数
互为相反数,化简即可得到x-y=b. 由此达到
化简方程组的目的.导引:做一做①+②,得27x+27y=81.化简,得x+y=3.③
①-②,得-x+y=-1.④
③+④,得2y=2,y=1.
③-④,得2x=4,x=2.
所以这个方程组的解是解:做一做 形如 的方程组,其求解过程可以总结为四步:
第一步,①+②,得到x+y=m③的形式;
第二步,①-②,得到x-y=n④的形式;
第三步,③+④;
第四步,③-④.
或者
第一步,①+②得到x+y=m③;
第二步,由③得x=m-y或y=m-x④;
第三步,将④代入方程②或①求解即可.总结归纳1 (中考·河北)利用加减消元法解方程组
下列做法正确的是( )
A.要消去y,可以将①×5+②×2
B.要消去x,可以将①×3+②×(-5)
C.要消去y,可以将①×5+②×3
D.要消去x,可以将①×(-5)+②×2
中考链接用加减法解方程组.
(1)(中考·东营)
(2)(中考·荆州) 2中考链接3 解方程组:
(1)(中考·无锡)
用整体代入法解方程组1用换元法解方程组:2课堂练习加减消元法的定义:
当二元一次方程组的两个方程中同一未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称加减法.课堂小结解方程组时,要根据方程组的特点,选择合适的解法:
(1)当方程组中存在一个方程的某一个未知数系数的绝对值是1或有一个方程的常数项是0时,一般用代入法;
(2)当两个方程中某一个未知数系数的绝对值相等或成整数倍关系时,一般用加减法.用加减消元法解二元一次方程组的一般步骤: (1)变形:将方程组中某一未知数的系数变为相等或
相反.
(2)加减:消去一个未知数.
(3)求解:得到一个未知数的值.
(4)回代:求另一个未知数的值.
(5)写出解.课堂小结完成教材P43作业题T1-T5课后作业谢 谢
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
