2.4 二元一次方程组的应用——几大题型考查 课件
文档属性
| 名称 | 2.4 二元一次方程组的应用——几大题型考查 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-13 18:31:13 | ||
图片预览











文档简介
课件36张PPT。第二章 二元一次方程组2.4 二元一次方程组的应用
——几大题型考查回顾旧知 审→设→找→列→解→验→答
(1)审:审题,分析题中已知什么,求什么,明确各数量之
间的关系
(2)设:设未知数(一般求什么,就设什么为x,y)
(3)找:找出能够表示应用题全部意义的两个等量关系
(4)列:根据这两个等量关系列出需要的代数式,进而列出两
个方程,组成方程组
(5)解:解所列方程组,得未知数的值
(6)验:检验所求未知数的值是 否符合题意,是否符合实际
(7)答:写出答案(包括单位名称)列二元一次方程组解应用题的一般步骤:今天重点学习二元一次方程组的应用的几大题型考查二元一次方程组的应用的几大题型考查合作学习行程问题
工程问题
图表信息问题
几何图形问题
增长率问题
百分比问题
方案优化问题
分段计费问题1. 张明沿公路匀速前进,每隔4 min就遇到迎面开来的一辆公共汽车,每隔6 min就有一辆公共汽车从背后超过他. 假定公共汽车的速度不变, 而且迎面开来的相邻两车的距离和从背后开来的相邻两车的距离都是1 200 m,求张明前进的速度和公共汽车的速度.题型1:相遇(追及)问题行程问题分析:
(1)“相向而遇”时,两者所走的路程之和等于两者原来的距离;
(2)“同向追及”时,快者所走的路程减去慢者所走的路程等于两者原来的距离.设张明前进的速度是x m/min,公共汽车的速度是y m/min.
根据题意,得
解这个方程组,得
答:张明前进的速度是50 m/min,公共汽车的速
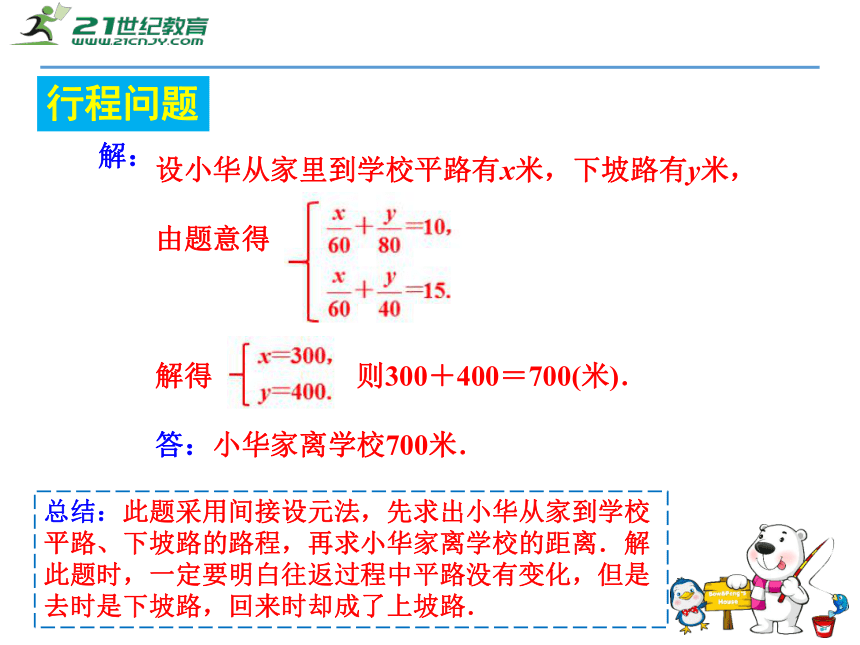
度是250 m/min.解:行程问题2.小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60 米,下坡路每分钟走80 米,上坡路每分钟走40 米,则他从家里到学校需10 分钟,从学校到家里需15 分钟. 问:从小华家到学校的平路和下坡路各有多远?题型2:上、下坡问题行程问题设小华从家里到学校平路有x米,下坡路有y米,
由题意得
解得 则300+400=700(米).
答:小华家离学校700米.解:行程问题总结:此题采用间接设元法,先求出小华从家到学校平路、下坡路的路程,再求小华家离学校的距离.解此题时,一定要明白往返过程中平路没有变化,但是去时是下坡路,回来时却成了上坡路.3.一列载客火车和一列运货火车分别在两条平行的铁轨上行驶,载客火车长150 m,运货火车长250 m.若两车相向而行.从车头相遇到车尾离开共需10 s;若载客火车从后面追赶运货火车,从车头追上运货火车车尾到完全超过运货火车共需100 s,试求两车的速度.题型3:错车问题行程问题设载客火车的速度为x m/s,运货火车的速度
为y m/s.由题意,得 解得
答:载客火车的速度是22 m/s,运货火车的速
度是18 m/s.解:总结:
本题是一道特殊的相遇与追及结合的应用题.①两车相向而行是相遇问题,相遇时两车行驶的路程总和=两车车身长之和;②载客火车从后面追赶运货火车是追及问题,追上时两车所走的路程差=两车车身长之和.
错车问题属于特殊的行程问题,它与行程问题的主要区别是:行程问题不考虑车本身的长,而错车问题要考虑车本身的长.与错车问题类似的还有过桥问题、过隧道问题等.行程问题4. A,B两地相距80 千米,一艘船从A地出发顺水航行4小时到达B地,而从B地出发逆水航行5小时到达A地,已知船顺水航行、逆水航行的速度分别为船在静水中的速度与水流速度的和与差,求船在静水中的速度和水流速度.题型4:航行问题行程问题设船在静水中的速度为x千米/时,水流速度为
y千米/时,由题意得
解得
答:船在静水中的速度为18千米/时,水流速度
为2千米/时.解:1.小明家准备装修一套房子,若请甲、乙两个装修公司合作,则需6 周完成,需花费工钱5.2 万元;若先请甲公司单独做4 周后,剩下的请乙公司来做,则还需9 周才能完成,需花费工钱4.8 万元.若只请一个公司单独完成,从节约开支的角度来考虑,小明家应该选甲公司还是乙公司?题型1:总量为1的问题工程问题设甲公司每周的工作效率为x,乙公司每周的工
作效率为y. 依题意,得 解得
即甲公司单独完成需10周,乙公司单独完成需15周.解:设请甲公司工作一周需花费工钱a万元,请乙公司工作一周需花费工钱b万元,依题意,得
解得
∴请甲公司单独完成需花费工钱10×0.6=6(万元),请乙公司单独完成需花费工钱15× =4(万元).
答:从节约开支的角度来考虑,小明家应该选乙公司.工程问题2.某服装厂接到生产一种工作服的订货任务,要求在规定期限内完成,按照这个服装厂原来的生产能力,每天可生产这种工作服150 套,按这样的生产进度,在客户要求的期限内只能完成订货量的
;现在工厂改进了人员结构和生产流程,每天可生产这种工作服200 套,这样不仅比规定时间少用1 天,而且比订货量多生产25 套,求要定做的工作服是多少套,要求的期限是多少天.题型2:总量不为1的问题工程问题设要定做的工作服是x套,要求的期限是y天,
依题意,得 解得
答:要定做的工作服是3 375套,要求的期限是18天.解:工程问题总结:
工效问题与行程问题相类似,关键是抓住三个基本量的关系,即“工作量=工作时间×工作效率”以及它们的变式“工作时间=工作量÷工作效率,工作效率=工作量÷工作时间”.注意当题目与工作量大小、多少无关时,通常用“1”表示总工作量.1.(中考·绍兴)图①的等臂天平呈平衡状态,其中左侧
秤盘有一袋石头,右侧秤盘有一袋石头和2个各10
克的砝码.将左侧袋中一颗石头移至右侧秤盘,并
拿走右侧秤盘的1个砝码后,天平仍呈平衡状态,
如图②所示.则被移动石头的质量为( )
A.5克 B.10克 C.15克 D.20克A图表信息问题2.(中考·吉林)根据图中的信息,求梅花鹿和长颈鹿现在的高度.设梅花鹿高x m,
长颈鹿高y m,
由题意得
解得
答:梅花鹿和长颈鹿现在的高度分别为1.5 m,
5.5 m.解:图表信息问题1. (中考·漳州)水仙花是漳州市花,如图,在长为14 m,宽为10 m的长方形展厅,划出三个形状、大小完全一样的小长方形摆放水仙花,则每个小长方形的周长为________m.16几何图形问题分析:
设小长方形的长为x m,宽为y m,则由题意可
知 两式相加可得x+y=8.
故小长方形的周长为2(x+y)=2×8=16(m).2.(中考·十堰)如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍,如果搭建正三角形和正六边形共用了2 016根火柴棍,并且正三角形的个数比正六边形的个数多6个,那么能连续搭建正三角形的个数是( )
A.222 B.280 C.286 D.292D几何图形问题3.小强用8 个边长不全相等的正三角形拼成如图所示的图案,其中阴影部分是边长为1 cm
的正三角形.试求出图中正三角形A、
正三角形B的边长分别是多少厘米.设正三角形A的边长为x cm,正三角形B的边长为
y cm,根据题意,得
解得
答:正三角形A的边长为3 cm,正三角形B的边长
为6 cm.解:几何图形问题总结:
本题渗透数形结合思想,易知正三角形A,H,G的边长相等,且正三角形B的边长=正三角形A的边长×2;正三角形F,E的边长相等,正三角形D,C的边长也相等,且正三角形F的边长=正三角形G的边长+1 cm,正三角形D的边长=正三角形E的边长+1 cm,正三角形B的边长=正三角形C的边长+1 cm,从而可得正三角形B的边长=正三角形A的边长+3 cm.分别设出正三角形A,B的边长,依此可列二元一次方程组,求出方程组的解即可得出答案.几何图形问题4.小敏做拼图游戏时发现:8 个一样大小的小长方形恰好可以拼成一个大的长方形,如图①所示.小颖看见了,也来试一试,结果拼成了如图②所示的正方形,不过中间留下了一个边长为2 cm的小正方形空白,你能算出每个小长方形的长和宽各是多少吗?几何图形问题设每个小长方形的长为x cm,
宽为y cm,
由题意得 解得
答:每个小长方形的长为10 cm,宽为6 cm.解:(中考·滨州)某公园六一期间举行特优读书游园活动,成人票和儿童票均有较大的折扣,张凯、李利都随他们的家人参加了本次活动,王斌也想去,就打听张凯、李利买门票花了多少钱.张凯说他家去了3个大人和4个小孩,共花了38元钱;李利说他家去了4个大人和2个小孩,共花了44元钱.王斌家计划去3个大人和2个小孩,请你帮他算一下,需准备________元钱买门票.34增长率问题分析:设成人票每张x元,儿童票每张y元,根据
题意得 解得
∴3x+2y=3×10+2×2=34.2.(中考·娄底)体育文化用品商店购进篮球和排球共20个,进价和售价如下表,全部销售完后共获利润260元.
(1)购进篮球和排球各多少个?
(2)销售6个排球的利润与销售几个篮球的利润相
等?增长率问题(1)设购进篮球x个,购进排球y个,由题意得:
解得
答:购进篮球12个,购进排球8个.解:增长率问题(2)设销售6个排球的利润与销售a个篮球的利润相等,
由题意得:6×(60-50)=(95-80)a,
解得a=4.
答:销售6个排球的利润与销售4个篮球的利润相等.1.某中学现有学生4 200人,计划一年后初中在校学生增加8%,高中在校学生增加11%,这样全校在校学生将增加10%,则该学校现有初中在校学生多少人?高中在校学生多少人?百分比问题设该校现有初中在校学生x人,高中在校学生y人.根据题意,
得 解得
答:该校现有初中在校学生1 400人,高中在校
学生2 800人.解:1.某电脑公司有A,B,C三种型号的电脑,其价格分别为A型每台6 000 元,B型每台4 000 元,C型每台2 500 元.某中学计划将100 500 元钱全部用于从该电脑公司购进其中两种不同型号的电脑共36台,请你设计出几种不同的购买方案供该校选择.方案优化问题设从该电脑公司购进A,B,C三种型号的电
脑的数量分别为x台、y台、z台.
(1)只购进A型和B型电脑,依题意,
得
解得 (不合题意,舍去)解:方案优化问题(2)只购进A型和C型电脑,依题意,
得 解得(3)只购进B型和C型电脑,依题意,
得
解得
所以有两种购买方案可供该校选择,
第一种方案是购进A型电脑3台和C型电脑33台;
第二种方案是购进B型电脑7台和C型电脑29台.方案优化问题总结:
设计方案问题应从不同角度去考虑,先考虑多种方案的可能,再列方程组,解方程组,根据结果合理地选择购买方案,本题有三种可能的选择,即只购买A与B型电脑、只购买B与C型电脑、只购买A与C型电脑,分别按题意建立方程组即可做出选择.方案优化问题A.阶梯电(水)价问题
1.为建设节约型、环境友好型社会,克服因干旱而造成的电力紧张困难,切实做好节能减排工作.某地决定对居民家庭用电实行“阶梯电价”,电力公司规定:居民家庭月用电量在80 千瓦时以下(含80 千瓦时,1 千瓦时俗称1度)时,实行“基本电价”;当居民家庭月用电量超过80 千瓦时时,超过部分实行“提高电价”.
小张家2014 年4 月份用电100 千瓦时,缴电费68 元;5 月份用电120 千瓦时,缴电费88 元.求“基本电价”和“提高电价”分别为多少.分段计费问题设“基本电价”为x元/千瓦时,“提高电价”
为y元/千瓦时,根据题意,得
解得
答:“基本电价”为0.6元/千瓦时,“提高电价”
为1元/千瓦时.解:分段计费问题B.出租车计费问题
2.某城市规定:出租车起步价允许行驶的最远路
程为3 千米,超过3 千米的部分按每千米(不足1
千米按1千米计算)另收费.甲说:“我乘这种
出租车行驶了11 千米,付了17 元.”乙说:
“我乘这种出租车行驶了23 千米, 付了35 元. ”
请你算一算这种出租车的起步价是多少元?超
过3 千米后每千米收费多少元?分段计费问题设这种出租车的起步价是x元,超过3千米后每千米收费y元,根据题意,得
解得
答:这种出租车的起步价是5元,超过3千米后每
千米收费1.5元.解:分段计费问题C.通信计费问题
3.某通信运营商的短信收费标准如下:发送网内
短信0.1 元/条,发送网外短信0.15 元/条.该通
信运营商的用户小王某月发送以上两种短信共
计150 条,依照该收费标准共支出短信费用19
元.问小王该月发送网内、网外短信各多少
条?分段计费问题设小王该月发送网内短信x条,网外短信y条.
根据题意,得
解这个方程组得
答:小王该月发送网内短信70条,网外短信80条.解:分段计费问题完成练习册对应的练习课后作业谢 谢
——几大题型考查回顾旧知 审→设→找→列→解→验→答
(1)审:审题,分析题中已知什么,求什么,明确各数量之
间的关系
(2)设:设未知数(一般求什么,就设什么为x,y)
(3)找:找出能够表示应用题全部意义的两个等量关系
(4)列:根据这两个等量关系列出需要的代数式,进而列出两
个方程,组成方程组
(5)解:解所列方程组,得未知数的值
(6)验:检验所求未知数的值是 否符合题意,是否符合实际
(7)答:写出答案(包括单位名称)列二元一次方程组解应用题的一般步骤:今天重点学习二元一次方程组的应用的几大题型考查二元一次方程组的应用的几大题型考查合作学习行程问题
工程问题
图表信息问题
几何图形问题
增长率问题
百分比问题
方案优化问题
分段计费问题1. 张明沿公路匀速前进,每隔4 min就遇到迎面开来的一辆公共汽车,每隔6 min就有一辆公共汽车从背后超过他. 假定公共汽车的速度不变, 而且迎面开来的相邻两车的距离和从背后开来的相邻两车的距离都是1 200 m,求张明前进的速度和公共汽车的速度.题型1:相遇(追及)问题行程问题分析:
(1)“相向而遇”时,两者所走的路程之和等于两者原来的距离;
(2)“同向追及”时,快者所走的路程减去慢者所走的路程等于两者原来的距离.设张明前进的速度是x m/min,公共汽车的速度是y m/min.
根据题意,得
解这个方程组,得
答:张明前进的速度是50 m/min,公共汽车的速
度是250 m/min.解:行程问题2.小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60 米,下坡路每分钟走80 米,上坡路每分钟走40 米,则他从家里到学校需10 分钟,从学校到家里需15 分钟. 问:从小华家到学校的平路和下坡路各有多远?题型2:上、下坡问题行程问题设小华从家里到学校平路有x米,下坡路有y米,
由题意得
解得 则300+400=700(米).
答:小华家离学校700米.解:行程问题总结:此题采用间接设元法,先求出小华从家到学校平路、下坡路的路程,再求小华家离学校的距离.解此题时,一定要明白往返过程中平路没有变化,但是去时是下坡路,回来时却成了上坡路.3.一列载客火车和一列运货火车分别在两条平行的铁轨上行驶,载客火车长150 m,运货火车长250 m.若两车相向而行.从车头相遇到车尾离开共需10 s;若载客火车从后面追赶运货火车,从车头追上运货火车车尾到完全超过运货火车共需100 s,试求两车的速度.题型3:错车问题行程问题设载客火车的速度为x m/s,运货火车的速度
为y m/s.由题意,得 解得
答:载客火车的速度是22 m/s,运货火车的速
度是18 m/s.解:总结:
本题是一道特殊的相遇与追及结合的应用题.①两车相向而行是相遇问题,相遇时两车行驶的路程总和=两车车身长之和;②载客火车从后面追赶运货火车是追及问题,追上时两车所走的路程差=两车车身长之和.
错车问题属于特殊的行程问题,它与行程问题的主要区别是:行程问题不考虑车本身的长,而错车问题要考虑车本身的长.与错车问题类似的还有过桥问题、过隧道问题等.行程问题4. A,B两地相距80 千米,一艘船从A地出发顺水航行4小时到达B地,而从B地出发逆水航行5小时到达A地,已知船顺水航行、逆水航行的速度分别为船在静水中的速度与水流速度的和与差,求船在静水中的速度和水流速度.题型4:航行问题行程问题设船在静水中的速度为x千米/时,水流速度为
y千米/时,由题意得
解得
答:船在静水中的速度为18千米/时,水流速度
为2千米/时.解:1.小明家准备装修一套房子,若请甲、乙两个装修公司合作,则需6 周完成,需花费工钱5.2 万元;若先请甲公司单独做4 周后,剩下的请乙公司来做,则还需9 周才能完成,需花费工钱4.8 万元.若只请一个公司单独完成,从节约开支的角度来考虑,小明家应该选甲公司还是乙公司?题型1:总量为1的问题工程问题设甲公司每周的工作效率为x,乙公司每周的工
作效率为y. 依题意,得 解得
即甲公司单独完成需10周,乙公司单独完成需15周.解:设请甲公司工作一周需花费工钱a万元,请乙公司工作一周需花费工钱b万元,依题意,得
解得
∴请甲公司单独完成需花费工钱10×0.6=6(万元),请乙公司单独完成需花费工钱15× =4(万元).
答:从节约开支的角度来考虑,小明家应该选乙公司.工程问题2.某服装厂接到生产一种工作服的订货任务,要求在规定期限内完成,按照这个服装厂原来的生产能力,每天可生产这种工作服150 套,按这样的生产进度,在客户要求的期限内只能完成订货量的
;现在工厂改进了人员结构和生产流程,每天可生产这种工作服200 套,这样不仅比规定时间少用1 天,而且比订货量多生产25 套,求要定做的工作服是多少套,要求的期限是多少天.题型2:总量不为1的问题工程问题设要定做的工作服是x套,要求的期限是y天,
依题意,得 解得
答:要定做的工作服是3 375套,要求的期限是18天.解:工程问题总结:
工效问题与行程问题相类似,关键是抓住三个基本量的关系,即“工作量=工作时间×工作效率”以及它们的变式“工作时间=工作量÷工作效率,工作效率=工作量÷工作时间”.注意当题目与工作量大小、多少无关时,通常用“1”表示总工作量.1.(中考·绍兴)图①的等臂天平呈平衡状态,其中左侧
秤盘有一袋石头,右侧秤盘有一袋石头和2个各10
克的砝码.将左侧袋中一颗石头移至右侧秤盘,并
拿走右侧秤盘的1个砝码后,天平仍呈平衡状态,
如图②所示.则被移动石头的质量为( )
A.5克 B.10克 C.15克 D.20克A图表信息问题2.(中考·吉林)根据图中的信息,求梅花鹿和长颈鹿现在的高度.设梅花鹿高x m,
长颈鹿高y m,
由题意得
解得
答:梅花鹿和长颈鹿现在的高度分别为1.5 m,
5.5 m.解:图表信息问题1. (中考·漳州)水仙花是漳州市花,如图,在长为14 m,宽为10 m的长方形展厅,划出三个形状、大小完全一样的小长方形摆放水仙花,则每个小长方形的周长为________m.16几何图形问题分析:
设小长方形的长为x m,宽为y m,则由题意可
知 两式相加可得x+y=8.
故小长方形的周长为2(x+y)=2×8=16(m).2.(中考·十堰)如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍,如果搭建正三角形和正六边形共用了2 016根火柴棍,并且正三角形的个数比正六边形的个数多6个,那么能连续搭建正三角形的个数是( )
A.222 B.280 C.286 D.292D几何图形问题3.小强用8 个边长不全相等的正三角形拼成如图所示的图案,其中阴影部分是边长为1 cm
的正三角形.试求出图中正三角形A、
正三角形B的边长分别是多少厘米.设正三角形A的边长为x cm,正三角形B的边长为
y cm,根据题意,得
解得
答:正三角形A的边长为3 cm,正三角形B的边长
为6 cm.解:几何图形问题总结:
本题渗透数形结合思想,易知正三角形A,H,G的边长相等,且正三角形B的边长=正三角形A的边长×2;正三角形F,E的边长相等,正三角形D,C的边长也相等,且正三角形F的边长=正三角形G的边长+1 cm,正三角形D的边长=正三角形E的边长+1 cm,正三角形B的边长=正三角形C的边长+1 cm,从而可得正三角形B的边长=正三角形A的边长+3 cm.分别设出正三角形A,B的边长,依此可列二元一次方程组,求出方程组的解即可得出答案.几何图形问题4.小敏做拼图游戏时发现:8 个一样大小的小长方形恰好可以拼成一个大的长方形,如图①所示.小颖看见了,也来试一试,结果拼成了如图②所示的正方形,不过中间留下了一个边长为2 cm的小正方形空白,你能算出每个小长方形的长和宽各是多少吗?几何图形问题设每个小长方形的长为x cm,
宽为y cm,
由题意得 解得
答:每个小长方形的长为10 cm,宽为6 cm.解:(中考·滨州)某公园六一期间举行特优读书游园活动,成人票和儿童票均有较大的折扣,张凯、李利都随他们的家人参加了本次活动,王斌也想去,就打听张凯、李利买门票花了多少钱.张凯说他家去了3个大人和4个小孩,共花了38元钱;李利说他家去了4个大人和2个小孩,共花了44元钱.王斌家计划去3个大人和2个小孩,请你帮他算一下,需准备________元钱买门票.34增长率问题分析:设成人票每张x元,儿童票每张y元,根据
题意得 解得
∴3x+2y=3×10+2×2=34.2.(中考·娄底)体育文化用品商店购进篮球和排球共20个,进价和售价如下表,全部销售完后共获利润260元.
(1)购进篮球和排球各多少个?
(2)销售6个排球的利润与销售几个篮球的利润相
等?增长率问题(1)设购进篮球x个,购进排球y个,由题意得:
解得
答:购进篮球12个,购进排球8个.解:增长率问题(2)设销售6个排球的利润与销售a个篮球的利润相等,
由题意得:6×(60-50)=(95-80)a,
解得a=4.
答:销售6个排球的利润与销售4个篮球的利润相等.1.某中学现有学生4 200人,计划一年后初中在校学生增加8%,高中在校学生增加11%,这样全校在校学生将增加10%,则该学校现有初中在校学生多少人?高中在校学生多少人?百分比问题设该校现有初中在校学生x人,高中在校学生y人.根据题意,
得 解得
答:该校现有初中在校学生1 400人,高中在校
学生2 800人.解:1.某电脑公司有A,B,C三种型号的电脑,其价格分别为A型每台6 000 元,B型每台4 000 元,C型每台2 500 元.某中学计划将100 500 元钱全部用于从该电脑公司购进其中两种不同型号的电脑共36台,请你设计出几种不同的购买方案供该校选择.方案优化问题设从该电脑公司购进A,B,C三种型号的电
脑的数量分别为x台、y台、z台.
(1)只购进A型和B型电脑,依题意,
得
解得 (不合题意,舍去)解:方案优化问题(2)只购进A型和C型电脑,依题意,
得 解得(3)只购进B型和C型电脑,依题意,
得
解得
所以有两种购买方案可供该校选择,
第一种方案是购进A型电脑3台和C型电脑33台;
第二种方案是购进B型电脑7台和C型电脑29台.方案优化问题总结:
设计方案问题应从不同角度去考虑,先考虑多种方案的可能,再列方程组,解方程组,根据结果合理地选择购买方案,本题有三种可能的选择,即只购买A与B型电脑、只购买B与C型电脑、只购买A与C型电脑,分别按题意建立方程组即可做出选择.方案优化问题A.阶梯电(水)价问题
1.为建设节约型、环境友好型社会,克服因干旱而造成的电力紧张困难,切实做好节能减排工作.某地决定对居民家庭用电实行“阶梯电价”,电力公司规定:居民家庭月用电量在80 千瓦时以下(含80 千瓦时,1 千瓦时俗称1度)时,实行“基本电价”;当居民家庭月用电量超过80 千瓦时时,超过部分实行“提高电价”.
小张家2014 年4 月份用电100 千瓦时,缴电费68 元;5 月份用电120 千瓦时,缴电费88 元.求“基本电价”和“提高电价”分别为多少.分段计费问题设“基本电价”为x元/千瓦时,“提高电价”
为y元/千瓦时,根据题意,得
解得
答:“基本电价”为0.6元/千瓦时,“提高电价”
为1元/千瓦时.解:分段计费问题B.出租车计费问题
2.某城市规定:出租车起步价允许行驶的最远路
程为3 千米,超过3 千米的部分按每千米(不足1
千米按1千米计算)另收费.甲说:“我乘这种
出租车行驶了11 千米,付了17 元.”乙说:
“我乘这种出租车行驶了23 千米, 付了35 元. ”
请你算一算这种出租车的起步价是多少元?超
过3 千米后每千米收费多少元?分段计费问题设这种出租车的起步价是x元,超过3千米后每千米收费y元,根据题意,得
解得
答:这种出租车的起步价是5元,超过3千米后每
千米收费1.5元.解:分段计费问题C.通信计费问题
3.某通信运营商的短信收费标准如下:发送网内
短信0.1 元/条,发送网外短信0.15 元/条.该通
信运营商的用户小王某月发送以上两种短信共
计150 条,依照该收费标准共支出短信费用19
元.问小王该月发送网内、网外短信各多少
条?分段计费问题设小王该月发送网内短信x条,网外短信y条.
根据题意,得
解这个方程组得
答:小王该月发送网内短信70条,网外短信80条.解:分段计费问题完成练习册对应的练习课后作业谢 谢
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
