2.4 二元一次方程组的应用 课件

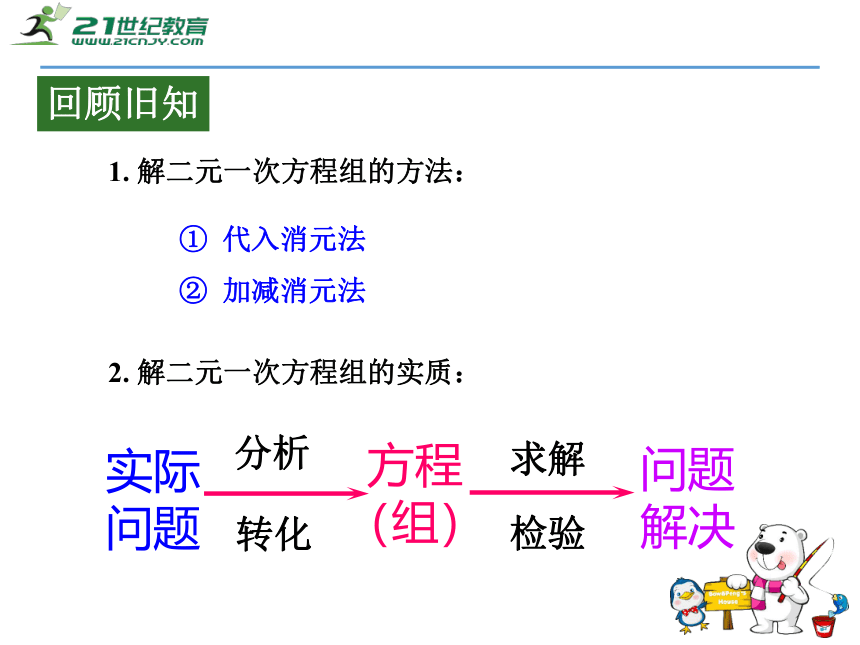
课件23张PPT。第二章 二元一次方程组2.4 二元一次方程组的应用回顾旧知1. 解二元一次方程组的方法：① 代入消元法
② 加减消元法实际问题问题解决检验求解方程（组）2. 解二元一次方程组的实质： 游泳池中有一群小朋友，男孩戴蓝色游泳帽，女
孩戴红色游泳帽. 如果每位男孩看到蓝色与红色的游
泳帽一样多, 而每位女孩
看到蓝色的游 泳帽比红
色的多1倍，你知道男孩
与女孩各有多少人吗？情境引入 我们该怎么解决这一问题，可以从哪几个方面进行思考？ 要解决这一问题，我们可以从以下几个方面进
行思考：
(1) 问题中所求的未知数有几个？
(2) 有哪些等量关系？
(3) 怎样设未知数？可以列出几个方程？
(4) 本题能列一元一次方程求解吗？用列二元一次方
程组的方法求解，有什么优点？情境引入用如图1中的长方形和正方形纸板作侧面和底面，做成如图 2的竖式和横式两种无盖纸盒. 现在仓库里有1000张正方形纸板和2000 张长方形纸板，问两种纸盒各做多少个，恰好将库存的纸板用完？例1例题讲解分析：做一个竖式纸盒需要几张长方形纸板和正方形
纸板？做一个横式纸盒呢？请填写下表：根据上表我们就能列出两个二元一次方程，解这
个二元一次方程组得到所求的解.例题讲解设做竖式纸盒x个，横式纸盒y个.根据题意，得解：①×4-②，得 5y=2 000, 解得y=400.
把y=400 代入①，得 x+800=1 000,
解得x=200.
所以方程组的解为
经检验，这个解满足方程组，且符合题意.
答: 做竖式纸盒200个，横式纸盒400个，恰好将库
存的纸板用完.例题讲解在刚才的过程中，经历了哪些步骤？（审题，搞清已知和未知，分析数量关系）
（考虑如何根据等量关系设元，列出方程组．）
（列出方程组并求解，得到答案）
（检查和反思解题过程，检验答案的正确性以及是
否符合题意）理解问题制定计划　执行计划回顾　总结归纳审、设、列、解、检例2 一根金属棒在0℃时的长度是q (m),温度每升高1℃,它就伸长p (m).当温度为t ℃时,金属棒的长度可用公式L=pt+q计算.已测得当t =100℃时,L=2.002m;当t =500℃时,L=2.01m.
(1)求p,q的值;
(2)若这根金属棒加热后长度伸长到2.016m,问这时金属棒的温度是多少?例题讲解分析：
①从所求出发,求p、q两个字母的值,必须列出几条方程？
②从已知出发,如何利用L=pt+q及两对已知量.
③在⑴题中求得字母系数p与q之后，就可以得到 L与 t 怎样的关系式？那么第⑵题中，已知 L＝2.016米时，如何求 t 的值。 解：（1）根据题意，得②-①,得400p=0.008解得p=0.00002把p=0.00002代入①，得0.002+q=2.002解得q=2答：p=0.00002,q=2（2）由（1），得L=0.00002t+2当L=2.016m时2.016=0.00002t+2解这个方程，得t=800答：此时金属棒的温度是800 ℃.例题讲解例题讲解例3 通过对一份中学生营养快餐的检测,得到以下信息:
① 快餐总质量为300 g;
② 快餐的成分:蛋白质、碳水化合物、脂肪、矿物质；
③ 蛋白质和脂肪含量占50%；矿物质的含量是脂肪
含量的2倍；蛋白质和碳水化合物含量占85%。根据上述数据回答下面的问题：
试分别求出营养快餐中蛋白质、碳水化合物、脂肪、矿物质的质量和所占百分比；解： 设一份营养快餐中含蛋白质x (g)脂肪y (g) ，则矿物质为2y (g) ，碳水化合物为（300×85%－x） (g) .
由题意，得①+②，得 3y=45,
解得 y＝15 (g).
∴ x=150－y=135 (g),2y=2×15=30(g),
300×85%－x＝255－135=120(g)想一想：你还能列出怎样的方程组？比较一下怎样的方程组更简便？例题讲解中学生营养快餐成分统计表例题讲解将以上中学生营养快餐成分绘制成表格如下：中学生营养快餐成分绘制成扇形统计图如右：有一个三位数，现将最左边的数字移到最右边，则比原来的数小45；又知原百位数字的9倍比由原十位数字和个位数字组成的两位数小3，求原三位数．1 拓展训练此题中的三位数，根据两个条件，可知不必设成三个未知数，只需把原三位数看成由一个百位数字x和一个由十位数字与个位数字组成的两位数y组成，则原三位数就可写成100x＋y；若将最左边百位数字移到最右边，则x就变成了个位数字，y就扩大为原来的10倍，新三位数可表示为10y＋x. 本题的等量关系为：(1)原百位数字×9＝由原十位数字与个位数字组成的两位数－3；(2)新三位数＝原三位数－45.分析：设原百位数字为x，由原十位数字与个位数字组
成的两位数为y，由题意，
得 解得
则4×100＋39＝439.
答：原三位数为439.解：拓展训练(1) 关键:正确地用代数式表示一个多位数.如一个三位数的表示方法，当它的百位数字为a，十位数字为b，个位数字为c时，这个三位数可表示为100a＋10b＋c.(2)在数字问题中，应注意：①数字与数的区别，即怎样用数字表示数；②根据数字的特点，求得的解应是小于10的非负整数(最高位上的数字不能为 0)．某中学七年级甲、乙两班共有93人，其中参加数学课
外兴趣小组的共有27人，已知甲班有 的学生参加
数学课外兴趣小组，乙班有 的学生参加数学课外兴趣小组，求这两个班级各有多少人．导引： 2本题的未知数有两个，即甲班的人数和乙班的人数；
本题所含的等量关系有：①甲班人数＋乙班人数＝
93；②甲班人数× ＋乙班人数× ＝27.拓展训练设甲班的人数为x人，乙班的人数为y人，根据题意，
得
解得
答：甲班的人数为48人，乙班的人数为45人．解： 拓展训练总结：设未知数时，一般是求什么就设什么，且所列方程的个数与未知数的个数相等．解这类问题的应用题，要抓住题中反映数量关系的关键词：和、差、倍、几分之几、比、大、小、多、少、增加、减少等，明确各种反映数量关系的关键词的含义．父亲给儿子出了一道题，要儿子猜出答案：有一对母
女，5年前母亲的年龄是女儿年龄的15倍，15年后，
母亲的年龄比女儿年龄的2倍只多6岁．那么现在这对
母女的年龄分别是多少？导引： 3先分别设出现在这对母女的年龄，再用它们表示出5
年前母女的年龄和15年后母女的年龄，则根据①5年
前，母亲的年龄是女儿年龄的15倍；②15年后，母
亲的年龄是女儿年龄的2倍再加6，列出方程组．列
表如下．拓展训练解：设现在这对母女的年龄分别是x岁和y岁，由题意，
得
则现在这对母女的年龄分别是35岁和7岁．解得拓展训练解答年龄问题的关键是年龄差不变及增长岁数相同．〈中考·南通〉有大小两种货车，3辆大车和4辆
小车一次可以运货22吨，2辆大车与6辆小车一
次可以运货23吨．
请根据以上信息，提出一个能用方程(组)解决
的问题，并写出这个问题的解答过程．1中考链接1．基本思想方法：
(1)列方程组解应用题是把“未知”转化成“已知”的过程；它的关键是把未知量与已知量联系起来，找出题目中的等量关系列方程组．(2)一般情况下，有几个未知量就必须列出几个方
程，所列方程必须满足：
①方程两边表示的是同类量；
②同类量的单位要统一；
③方程两边的数值要相等．总结归纳2. 列二元一次方程组解应用题的一般步骤：
审→设→找→列→解→验→答
(1)审：审题，分析题中已知什么，求什么，明确各数量之
间的关系
(2)设：设未知数(一般求什么，就设什么为x，y)
(3)找：找出能够表示应用题全部意义的两个等量关系
(4)列：根据这两个等量关系列出需要的代数式，进而列出两
个方程，组成方程组
(5)解：解所列方程组，得未知数的值
(6)验：检验所求未知数的值是 否符合题意，是否符合实际
(7)答：写出答案(包括单位名称)课堂小结1. 完成教材P46作业题T1-T5
2. 完成教材P49作业题T1-T6课后作业谢 谢