3.3多项式的乘法(1) 课件

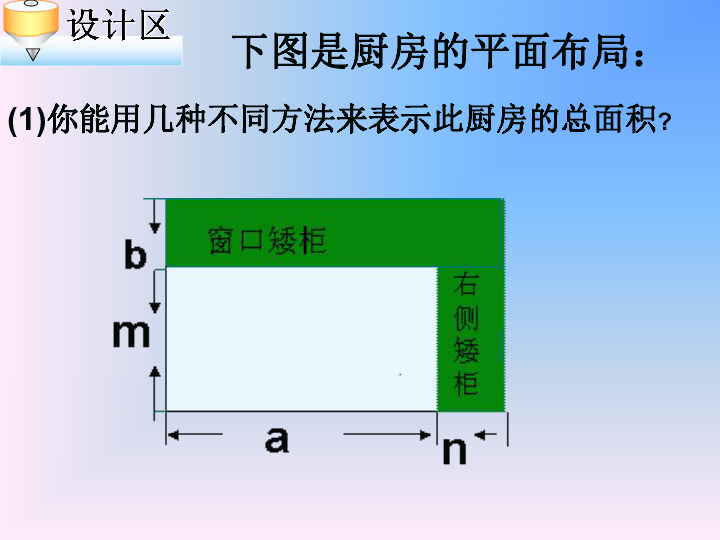
课件13张PPT。新课标教学网（www.xkbw.com）--海量教学资源欢迎下载！3.3 多项式的乘法美丽人生新课标教学网（www.xkbw.com）--海量教学资源欢迎下载！黄慧老师家买了新房子，要装修厨房,打算在厨房沿墙做一排矮柜,使厨房的空间得到充分的利用,而且便于清理.美丽人生下图是厨房的平面布局：(1)你能用几种不同方法来表示此厨房的总面积?多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.即(a+n)(b+m)=ab+am+nb+nm.
多项式乘法法则:应用区例1 计算: (1) (x+2y)(2a+3b) (2) (2x–3)(x+4) 是非区判断下列算式对错，对的打“√” ，错的打“×”(1) (2n+6)(n–3)=2n2+12n－18（ ）(2) (2x+3)(2x–3)= 4x2–9 （ ）(3) (2x+5)(2x+5)= 4x2+25 （ ） (4) (a+3)(2a–3)= 2a2–3a+ 6a–9（ ）×√××2n2－18符号漏乘4x2+20x+25化简2a2+ 3a–9(5) –(s+1)(a–b)= –as–bs+a–b ( )×没添括号＝–（as–bs+a–b）＝–as+bs – a+b操练区练习: (1)(3)(2) (3x+y)(x–2y) ；
(4) (xy–z)(2xy+z) ;巩固区例2 (1)、先化简,再求值:
(2a-3)(3a+1)-6a(a-4) 其中a=
（3）化简：(2x-1)(-3x)-(1-3x)(1+2x)－4x（2）先化简，再求值：
2(x+3)(x-3)-x(x-6),其中x=2感言区
1.多项式的乘法法则：多项式与多项式相乘,先用一个多项式的
每一项乘另一个多项式的每一项,再把所得的积相加。2.多项式的乘法法则在运用时要注意：
(1). 不漏乘
(2). 相乘时带符号
(3). 乘出来后要合并同类项
(4). 添括号巩固区5.若(x+a)(x+b)中不含x的一次项，则a与b的关系是 ( )
(A)a=b=0 (B)a-b=0 (C)a=b≠0 (D)a+b=04.已知 的结果中含　 的项的系数为0，则 的值为（ ）．
A、 -2 B、-4 C、1 D、以上均错AD拓展区解方程解：一元二次方程一元一次方程2x(x-3)-(x-3)(x+8)=x2+10拓展区 若(a + m) (a – 2 ) = a2 + na – 6 对 a 的任
何值都成立，求m,n值。 m = 3 , n = 1 解: (a + m) (a – 2 ) = a2 -2a+ma-2m
= a2 +(m-2)a-2m
∴n=m-2, -2m=-6