3.4乘法公式(2)课件

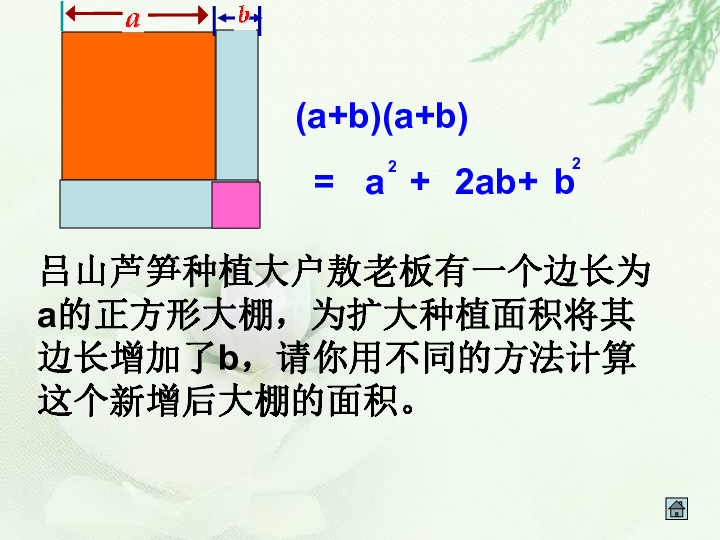
课件23张PPT。13.4乘法公式(二)完全平方公式2运用平方差公式计算:(1) (2x+1)(2x-1)(2)(-x+y)(-y-x)3(a+b)(a+b)2ab=++ab吕山芦笋种植大户敖老板有一个边长为a的正方形大棚，为扩大种植面积将其边长增加了b，请你用不同的方法计算这个新增后大棚的面积。4 两数和的平方,等于这两数的平方和 , 加上这两数积的2倍. (a+b)2=a2+2ab+b25(2)(2a+3b)2= ( )2 + 2( )( ) + ( )2(a + 1)2=( )2+2( )( )+ ( )2aa112a2a3b3b用两数和的完全平方公式计算(填空):(a + b)2 = a2 + 2 a b + b26 你能计算(a?b)2吗?自主探索 ?=a2?2a b+b2=a2+2a (?b)+ (?b)2解：(a?b)2
　　=[a+(?b)]22.用两数和的完全平方公式来计算解：(a?b)2
　= (a?b) (a?b)
　= a2?a b-ab+b2
　=a2?2a b+b21.直接计算7 两数差的平方,等于这两数的平方和,减去这两数积的2倍. (a?b)2=a2?2ab+b28a2ababb2(a+b)2 =a?ba?bab(a?b)2a2+2ab+b2即 (a?b)2 = a2?2ab+b2(a?b)2 = a2? ab ? ab+b2　　　　　　试一试
　你能由两数和的完全平方公式的几何意义推想到两数差的完全平方公式的几何意义吗？9 (a+b)2=a2+2ab+b2(a?b)2=a2?2ab+b2完全平方公式 两个数的和（或差）的平方，等于它们的平方和，加上（或减去）它们的积的2倍。首平方，尾平方，首尾两倍放中间10运用完全平方公式填表　(a±b)2=a2±2ab+b2－2·2a·52·(-2s) ·t11由表格可得：首尾平方总得正；
中间符号看首尾项的积，同号得正，
异号得负，中间的2倍要记牢；
进而总结步骤为：(1)、确定首尾，分别平方；
(2)、确定中间项的系数和符号；
(3)、写出结论。12 例1 利用完全平方公式计算：

(1) (2a+5)2 ； (2) (x－2y)2;

(3) (－2a+b)2 ; (4) (－3x－2y)213下列各式的计算是否有错？错的请改正。(1) (x+y)2 = x2 +y2(2) (a –b)2 = a2 -b2(4) (a+2b)2 = a2+2ab+2b2(3) (x– 1)2 = x2 – 2x (5) (2+x)2 = 2 + 4x+ x214请你直接应用完全平方公式计算：
1、（3+x)2 2、（y-7)2
3、（-2x-3y)2 4、（3- )2
15选择适当的公式计算：（1）、(2x-1)(-1+2x)
（2）、(-2x-y)(2x-y)
（3）、 (a+5)(-a-5)
（4）、(ab-1)(-ab+1)16例题例2：利用完全平方公式计算：
(1) 0.982 (2) 10012解：(1) 原式 = （ 1 ? 0.02）2= 12 ? 2 ×1×0.02 + 0.022= 1 ? 0.04 + 0.0004= 0.9604（2）原式 = （ 1000 + 1 ）2= 10002 + 2 × 1000×1 + 12= 1000000 + 2000 + 1=1002001171、运用完全平方公式计算：992
活用公式:2、如果x2-6x+N是一个完全平方式,那么N是( )
(A)36 (B)9 (C)-36 (D)-93、用简便的方法计算:
1.232+2.46×0.77+0.772 (4)已知(a+b)2=11,ab=1,求(a-b)2的值.18例题3.生活在线：一花农有1块正方形茶花苗圃，边长为am。现将这块苗圃的边长都增加1.5m，求这块苗圃的面积增加了多少m2。(a+1.5)2-a2=a2+3a+2.25-a2= 3a+2.2519练习1. 一花农有2块正方形茶花苗圃,
边长分别为 30.1 m , 29.5 m, 现将这2
块苗圃的边长都增加1.5m后,求各苗
圃的面积分别增加了多少m2?解：设原正方形苗圃的边长为a(m),
边长增加1.5m后,新正方形的边长
为(a+1.5)m；由题意可得，当a=30.1时，3a+2.25=3×30.1+2.25=92.55；
当a=29.5时，3a+2.25=3×29.5+2.25=90.75；
答：两块苗圃的面积分别增加了92.55平方米，90.75平方米。20例题4:化简21本节课你学到了什么?注意完全平方公式和平方差公式不同： 完全平方公式的结果 是三项，即
(a ± b)2＝a2 ± 2ab + b2. 平方差公式的结果 是两项，即
(a+b)(a?b)＝a2?b2. 有时需要进行变形，使变形后的式子符合应
用完全平方公式的条件，即为“两数和(或差)的平方”，然后应用公式计算. 在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2.22挑战自己3.如果 是一个完全平方式，那么a的值是( )
A.2 B.-2 C. 2 D. 1C23【1】、复习、整理、巩固今天所学知识。一、必做题：1、作业本(2)第16--19页T1—T7；
2、参书第78页A组题T1—T3；
3.课时特训第47、48页T1—T16；
二、选做题：1、参书第78页B、C组题T4—T6；
2.拓展探究题：参看幻灯片第32--36号。
三、抄写第20--30张幻灯片的内容。【2】、书面作业布置作业：