3.1 同底数幂的乘法(3)—积的乘方 课件
文档属性
| 名称 | 3.1 同底数幂的乘法(3)—积的乘方 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 191.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-27 00:00:00 | ||
图片预览






文档简介
课件16张PPT。幂的意义:an=am+n 幂的乘方法则:(am)n= (m、n都是正整数)amn复习回顾① a3·a4· a = ( )
②(a3)5 = ( )
③ 3×a2×5 = ( )
a8 a15 15a2 同底数幂相乘 幂的乘方 乘法交换律、结合律 正确写出得数,并说出是属于哪一种幂的运算。 3.1 同底数幂的乘法(3)—积的乘方探索与交流 (4×6)3 =( )·( )·( )
=( ) ·( )
=4( ) ×6( ) ( ) 根据乘方的意义和同底数幂的乘法法则填空4×64×64×6( )乘方的意义4×4×46×6×6( )乘法交换律、结合律 33幂的意义 (4×6)5 =( )·( )·( )·( )·( )
=( ) ·( )
=4( ) ×6( )4×64×64×64×4×4×4×46×6×6×6×6554×64×6 (ab)4 =( )·( )·( )·( )
=( ) ·( )
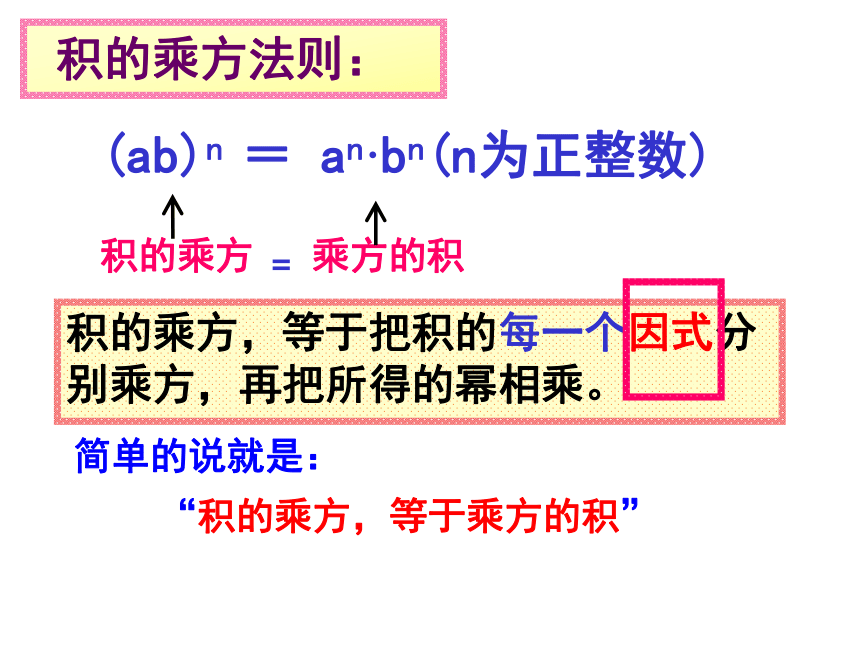
=a( ) ×b( )abababa·a·a·a44abb·b·b·b你能归纳出积的乘方法则吗?=anbn猜想:(n为正整数)(ab)n = an·bn(n为正整数)
积的乘方 乘方的积 积的乘方法则:积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘。 简单的说就是:
“积的乘方,等于乘方的积” = (abc)n= (n为正整数) anbncn 65页想一想公式拓展三个或三个以上的积的乘方,是否也具有上面的性质? 例题解析例题解析【例4】计算:
(1)(2b)5; (2)(3x3)6; (3)(-x3y2 )3; (4) =25b5 = 32b5 (1) (2b)5解:(2) (3x3)6 = 36 ( x3 ) 6= 36x18(3) (-x3 y2 ) 3 = -(x3 )3 ( y2 )3= - x9 y6(4)= 729x18 (1)分别乘方前,要看清各因式.
(2)因式可为数、单项式、多项式.
(3)对于底数有多个因式时此法则也适用.
如:(2a)3如:(2×3)4、[x(x+y)]5如:(abc)n=anbncn注意想一想:下面的计算对吗?错的请改正:××××××例题解析例题解析【例5】木星是太阳系八大行星中最大的一颗,木星可以近似地看做球体。已知木星的半径大约是7×104 km,求木星的体积(结果精确到 )解:=×(7×104)373×1012(km3)注意
运算顺序 !答:木星的体积大约是 1.4 ×1015 km3 ≈1.4 ×1015
(ab)n = an·bn (n都是正整数)反向使用:an·bn = (ab)n 小结反向使用am · an =am+n、(am)n =amn 可使某些计算简捷。 每个因式分别乘方后的积 应用积的乘方法则要注意积的每一个因式都要乘方,特别是要注意数字因数也要乘方 用简便方法计算:(1)(-0.25)17 ·(-4)17(2)( )2008 ·(-2 )2009 (3)82×42009×(-0.25)2009 13535想一想2.若Xa=2, Xb=3, 求(x3a+2b)2的值.1.已知x =2,y =3,求(x 2 y) 的值。2nnn
②(a3)5 = ( )
③ 3×a2×5 = ( )
a8 a15 15a2 同底数幂相乘 幂的乘方 乘法交换律、结合律 正确写出得数,并说出是属于哪一种幂的运算。 3.1 同底数幂的乘法(3)—积的乘方探索与交流 (4×6)3 =( )·( )·( )
=( ) ·( )
=4( ) ×6( ) ( ) 根据乘方的意义和同底数幂的乘法法则填空4×64×64×6( )乘方的意义4×4×46×6×6( )乘法交换律、结合律 33幂的意义 (4×6)5 =( )·( )·( )·( )·( )
=( ) ·( )
=4( ) ×6( )4×64×64×64×4×4×4×46×6×6×6×6554×64×6 (ab)4 =( )·( )·( )·( )
=( ) ·( )
=a( ) ×b( )abababa·a·a·a44abb·b·b·b你能归纳出积的乘方法则吗?=anbn猜想:(n为正整数)(ab)n = an·bn(n为正整数)
积的乘方 乘方的积 积的乘方法则:积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘。 简单的说就是:
“积的乘方,等于乘方的积” = (abc)n= (n为正整数) anbncn 65页想一想公式拓展三个或三个以上的积的乘方,是否也具有上面的性质? 例题解析例题解析【例4】计算:
(1)(2b)5; (2)(3x3)6; (3)(-x3y2 )3; (4) =25b5 = 32b5 (1) (2b)5解:(2) (3x3)6 = 36 ( x3 ) 6= 36x18(3) (-x3 y2 ) 3 = -(x3 )3 ( y2 )3= - x9 y6(4)= 729x18 (1)分别乘方前,要看清各因式.
(2)因式可为数、单项式、多项式.
(3)对于底数有多个因式时此法则也适用.
如:(2a)3如:(2×3)4、[x(x+y)]5如:(abc)n=anbncn注意想一想:下面的计算对吗?错的请改正:××××××例题解析例题解析【例5】木星是太阳系八大行星中最大的一颗,木星可以近似地看做球体。已知木星的半径大约是7×104 km,求木星的体积(结果精确到 )解:=×(7×104)373×1012(km3)注意
运算顺序 !答:木星的体积大约是 1.4 ×1015 km3 ≈1.4 ×1015
(ab)n = an·bn (n都是正整数)反向使用:an·bn = (ab)n 小结反向使用am · an =am+n、(am)n =amn 可使某些计算简捷。 每个因式分别乘方后的积 应用积的乘方法则要注意积的每一个因式都要乘方,特别是要注意数字因数也要乘方 用简便方法计算:(1)(-0.25)17 ·(-4)17(2)( )2008 ·(-2 )2009 (3)82×42009×(-0.25)2009 13535想一想2.若Xa=2, Xb=3, 求(x3a+2b)2的值.1.已知x =2,y =3,求(x 2 y) 的值。2nnn
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
