3.5 整式的化简课件
图片预览

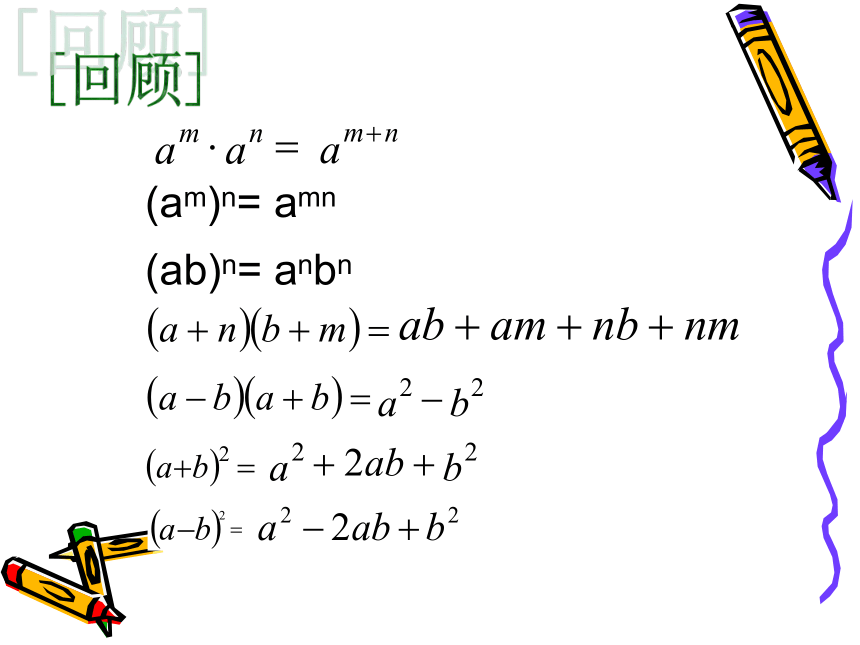

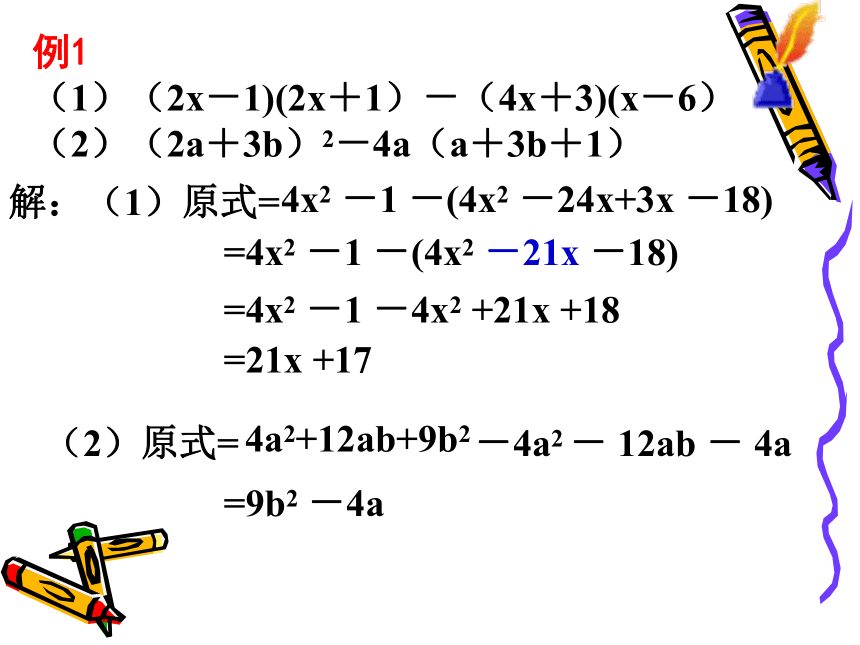



文档简介
课件15张PPT。第三章 整式的乘除3.5 整式的化简(am)n=amn(ab)n=anbn[回顾] 整式的化简应遵循先乘方、再乘除、
最后算加减的顺序。能运用乘法公式的则运用公式。整式化简运算顺序:例1
(1)(2x-1)(2x+1)-(4x+3)(x-6)
(2)(2a+3b)2-4a(a+3b+1)解:(1)原式=4x2 -1 -=4x2 -1 -(4x2 -21x -18)=4x2 -1 -4x2 +21x +18=21x +17(2)原式=4a2+12ab+9b2=9b2 -4a(4x2 -24x+3x -18)-4a2 - 12ab - 4a试一试2.当 时,求第1题中代数式的值。1、化简3. 化简(a+b+3)(a+b-3) 如图,点M是AB的中点,点P在MB上,分别以AP,PB为边,作正方形APCD和正方形PBEF.设AB=4a,MP=b,正方形APCD与正方形PBEF的面积之差为S.
(1)用a,b的代数式表示AP,BP;
(1)用a,b的代数式表示AP,BP;(2)用a,b的代数式表示S;整式通常要化简;
化简对于求值可以带来简便(1)、
(2)、
练习:化简求值1. 一辆自行车原价a元,降价x%,则
现价为_______元。a(1-x%)2. 一辆自行车原价a(1-x%)元,降价x%,则现价为_________元。a(1-x%)23. 一辆自行车原价a元,连续两次涨价
x%,则现价为_________元。a(1+x%)2例2:甲.乙两家超市3月份销售额均为a万元,
在4月和5月两个月中,甲超市的销售额平均每月增长x%,而乙超市的销售额平均每月减少x%.(1)5月份甲超市的销售额比乙超市多多少?(2)如果a=150,x=2,那么5月份甲超市的销售额比乙超市多多少万元? 实际应用 a a a(1+x%) a(1-x%) a(1+x%) (1+x%)
= a(1+x%)2 a(1-x%) (1-x%) = a(1-x%)2 我们一起努力!甲、乙两家超市3月份的销售额均为a万元,在4月和5月这两个月中,甲超市的销售额平均每月增长x%,而乙超市的销售额平均每月减少x%。
(1)5月份甲超市的销售额比乙超市多多少?(2)如果a=150,x=2,那么5月份甲超市的销售额
比乙超市多多少万元?学科网zxxk2.已知x+y=3,xy=1,求x2+y2与(x-y)2的值.3.已知x2+y2 -4x-6y+13=0,求x-y
的值.探索拓展,
挑战自我观察下列各式:
52=25
152=225
252=625
352=1225
……
52=25
152=225
252=625
352=1225
452=2025
……
752=5625
852=7225 可写成 +25
可写成 +25
可写成 +25
可写成 +25
可写成 +25
……
可写成
可写成 100×1×(1+1)100×2×(2+1)100×3×(3+1)100×4×(4+1)(1)探索规律: 100×0×(0+1)(2)归纳、猜想 :
(3)根据上面的归纳、猜想,试计算:
20052= 。100×7×8 +25100×8×9 +254020025 (10n+5)2= 100n2+100n+25= 100n(n+1) +25课堂小结:一、你能说出这节课的收获吗?二、应用整式解决实际问题的基本过程:
最后算加减的顺序。能运用乘法公式的则运用公式。整式化简运算顺序:例1
(1)(2x-1)(2x+1)-(4x+3)(x-6)
(2)(2a+3b)2-4a(a+3b+1)解:(1)原式=4x2 -1 -=4x2 -1 -(4x2 -21x -18)=4x2 -1 -4x2 +21x +18=21x +17(2)原式=4a2+12ab+9b2=9b2 -4a(4x2 -24x+3x -18)-4a2 - 12ab - 4a试一试2.当 时,求第1题中代数式的值。1、化简3. 化简(a+b+3)(a+b-3) 如图,点M是AB的中点,点P在MB上,分别以AP,PB为边,作正方形APCD和正方形PBEF.设AB=4a,MP=b,正方形APCD与正方形PBEF的面积之差为S.
(1)用a,b的代数式表示AP,BP;
(1)用a,b的代数式表示AP,BP;(2)用a,b的代数式表示S;整式通常要化简;
化简对于求值可以带来简便(1)、
(2)、
练习:化简求值1. 一辆自行车原价a元,降价x%,则
现价为_______元。a(1-x%)2. 一辆自行车原价a(1-x%)元,降价x%,则现价为_________元。a(1-x%)23. 一辆自行车原价a元,连续两次涨价
x%,则现价为_________元。a(1+x%)2例2:甲.乙两家超市3月份销售额均为a万元,
在4月和5月两个月中,甲超市的销售额平均每月增长x%,而乙超市的销售额平均每月减少x%.(1)5月份甲超市的销售额比乙超市多多少?(2)如果a=150,x=2,那么5月份甲超市的销售额比乙超市多多少万元? 实际应用 a a a(1+x%) a(1-x%) a(1+x%) (1+x%)
= a(1+x%)2 a(1-x%) (1-x%) = a(1-x%)2 我们一起努力!甲、乙两家超市3月份的销售额均为a万元,在4月和5月这两个月中,甲超市的销售额平均每月增长x%,而乙超市的销售额平均每月减少x%。
(1)5月份甲超市的销售额比乙超市多多少?(2)如果a=150,x=2,那么5月份甲超市的销售额
比乙超市多多少万元?学科网zxxk2.已知x+y=3,xy=1,求x2+y2与(x-y)2的值.3.已知x2+y2 -4x-6y+13=0,求x-y
的值.探索拓展,
挑战自我观察下列各式:
52=25
152=225
252=625
352=1225
……
52=25
152=225
252=625
352=1225
452=2025
……
752=5625
852=7225 可写成 +25
可写成 +25
可写成 +25
可写成 +25
可写成 +25
……
可写成
可写成 100×1×(1+1)100×2×(2+1)100×3×(3+1)100×4×(4+1)(1)探索规律: 100×0×(0+1)(2)归纳、猜想 :
(3)根据上面的归纳、猜想,试计算:
20052= 。100×7×8 +25100×8×9 +254020025 (10n+5)2= 100n2+100n+25= 100n(n+1) +25课堂小结:一、你能说出这节课的收获吗?二、应用整式解决实际问题的基本过程:
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
