1.3平行线的判定同步练习

浙教版七下数学1.3平行线的判定
一．选择题（共8小题）
1．如图，点E在CD延长线上，下列条件中不能判定AB∥CD的是（　　）
A．∠1=∠2 B．∠3=∠4 C．∠5=∠B D．∠B+∠BDC=180°
2．在同一平面内，有8条互不重合的直线，l1，l2，l3…l8，若l1⊥l2，l2∥l3，l3⊥l4，l4∥l5…以此类推，则l1和l8的位置关系是（　　）21cnjy.com
A．平行 B．垂直 C．平行或垂直 D．无法确定
3．如图，在下列给出的条件中，不能判定AB∥DF的是（　　）
A．∠A+∠2=180° B．∠1=∠A C．∠1=∠4 D．∠A=∠3
4．下列说法正确的是（　　）
A．两点之间的距离是两点间的线段
B．与同一条直线垂直的两条直线也垂直
C．同一平面内，过一点有且只有一条直线与已知直线平行
D．同一平面内，过一点有且只有一条直线与已知直线垂直
5．下列各图中，能画出AB∥CD的是（　　）
A．①②③ B．①②④ C．③④ D．①②③④
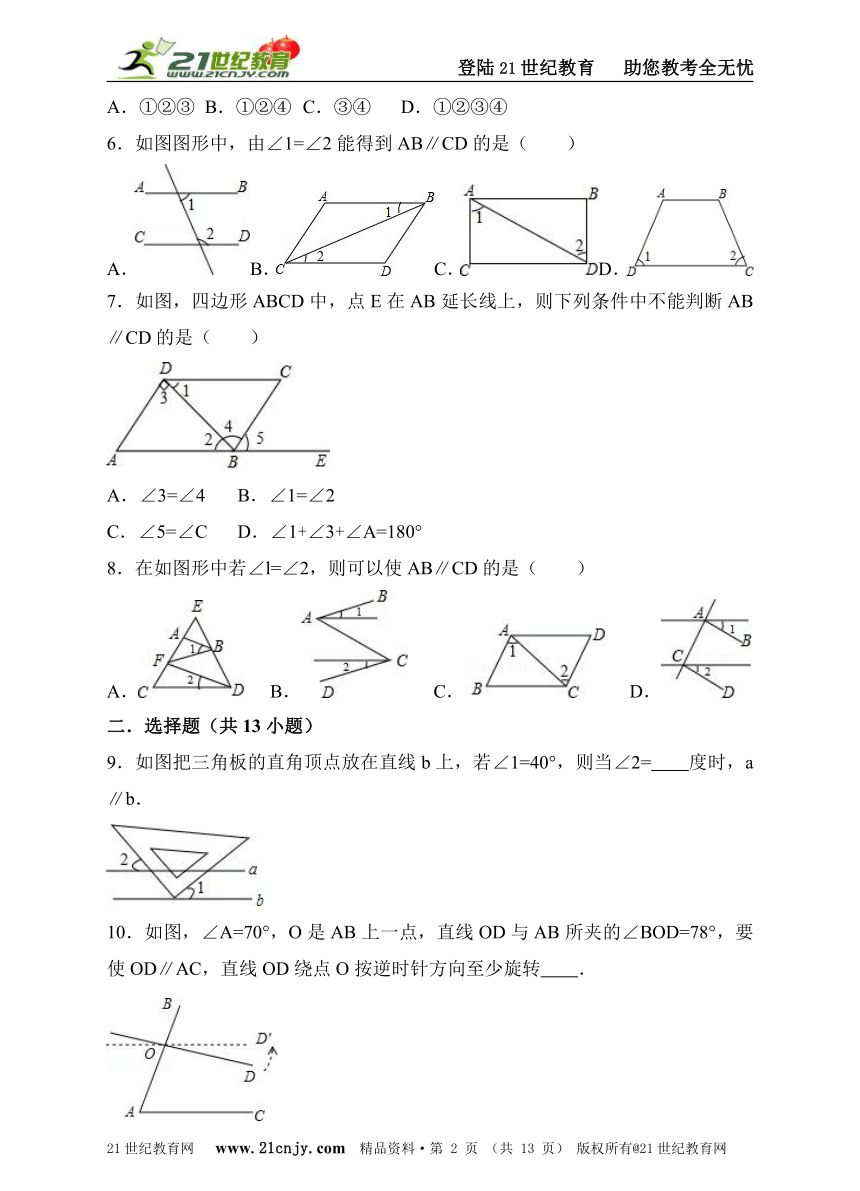
6．如图图形中，由∠1=∠2能得到AB∥CD的是（　　）
A．B．C．D．
7．如图，四边形ABCD中，点E在AB延长线上，则下列条件中不能判断AB∥CD的是（　　）
A．∠3=∠4 B．∠1=∠2
C．∠5=∠C D．∠1+∠3+∠A=180°
8．在如图形中若∠l=∠2，则可以使AB∥CD的是（　　）
A． B． C． D．
二．选择题（共13小题）
9．如图把三角板的直角顶点放在直线b上，若∠1=40°，则当∠2=　　度时，a∥b．
10．如图，∠A=70°，O是AB上一点，直线OD与AB所夹的∠BOD=78°，要使OD∥AC，直线OD绕点O按逆时针方向至少旋转　　．
11．如图是由五个同样的三角形组成的图案，三角形的三个角分别为36°，72°，72°，则图中共有　　对平行线．21·cn·jy·com
12．如图，已知∠ADE=60°，DF平分∠ADE，∠1=30°，试说明：DF∥BE．
解：∵DF平分∠ADE，（已知）
∴　　=∠ADE．（　　）
∵∠ADE=60°，（已知）
∴　　=30°．（　　）
∵∠1=30°，（已知）
∴　　，（　　）
∴　　，（　　）
13．如图，某工件要求AB∥ED，质检员小李量得∠ABC=146°，∠BCD=60°，∠EDC=154°，则此工件　　．（填“合格”或“不合格”）www.21-cn-jy.com
14．如图，下列条件中：
①∠B+∠BCD=180°；②∠1=∠2；③∠3=∠4；④∠B=∠5；
则一定能判定AB∥CD的条件有　　（填写所有正确的序号）．
15．如图，在下列条件中：①∠DAC=∠ACB；②∠BAC=∠ACD；③∠BAD+∠ADC=180°；④∠BAD+∠ABC=180°．其中能使直线AB∥CD成立的是　　．（填序号）2·1·c·n·j·y
16．下列说法中：①同位角相等；②过一个点有且只有一条直线与已知直线垂直；③两直线相交成的四个角中相邻两角的角平分线互相垂直；④三条直线两两相交，总有三个交点；⑤若a∥b，b∥c，则a∥c；⑥若a⊥b，b⊥c，则a⊥c．其中正确的说法是　　．21·世纪*教育网
17．如图所示，若AB∥CD，则∠1，∠2，∠3之间的关系是：　　．
18．如图所示，若AB∥CD，则∠E=　　．
19．如图，已知AE∥BD，∠1=3∠2，∠2=28°．求∠C=　　．
20．如图，已知AE∥BD，∠1=130°，∠2=30°，则∠ABD=　　，∠C=　　．
三．解答题（共3小题）
21．如图，一个由4条线段构成的“鱼”形图案，其中∠1=50°，∠2=50°，∠3=130°，找出图中的平行线，并说明理由．【来源：21·世纪·教育·网】
22．（1）画线段AC=30mm（点A在左侧）；
（2）以C为顶点，CA为一边，画∠ACM=90°；
（3）以A为顶点，AC为一边，在∠ACM的同侧画∠CAN=60°，AN与CM相交于点B；量得AB=　　mm；www-2-1-cnjy-com
（4）画出AB中点D，连接DC，此时量得DC=　　mm；请你猜想AB与DC的数量关系是：AB=　　DC2-1-c-n-j-y
（5）作点D到直线BC的距离DE，且量得DE=　　mm，请你猜想DE与AC的数量关系是：DE=　　AC，位置关系是　　．21*cnjy*com
23．如图，EF∥AD，AD∥BC，CE平分∠BCF，∠DAC=120°，∠ACF=20°，求∠FEC的度数．【出处：21教育名师】
　
浙教版七下数学1.3平行线的判定
参考答案与试题解析
　
一．选择题（共8小题）
1．解：选项B中，∵∠3=∠4，∴AB∥CD （内错角相等，两直线平行），所以正确；
选项C中，∵∠5=∠B，∴AB∥CD （内错角相等，两直线平行），所以正确；
选项D中，∵∠B+∠BDC=180°，∴AB∥CD（同旁内角互补，两直线平行），所以正确；
而选项A中，∠1与∠2是直线AC、BD被AD所截形成的内错角，因为∠1=∠2，所以应是AC∥BD，故A错误．【来源：21cnj*y.co*m】
故选A．
　
2．解：∵l2∥l3，l3⊥l4，l4∥l5，l5⊥l6，l6∥l7，l7⊥l8，
∴l2⊥l4，l4⊥l6，l6⊥l8，
∴l2⊥l8．
∵l1⊥l2，
∴l1∥l8．
故选A
　
3．解：A、∵∠2+∠A=180，∴AB∥DF（同旁内角互补，两直线平行）；
B、∵∠1=∠A，∴AC∥DE（同位角相等，两直线平行），不能证出AB∥DF；
C、∵∠1=∠4，∴AB∥DF（内错角相等，两直线平行）．
D、∵∠A=∠3，∴AB∥DF（同位角相等，两直线平行）
故选B．
　
4．解：A、两点之间的距离是指两点间的线段长度，而不是线段本身，错误；
B、在同一平面内，与同一条直线垂直的两条直线平行，错误；
C、同一平面内，过直线外一点有且只有一条直线与已知直线平行，应强调“直线外”，错误；
D、这是垂线的性质，正确．故选D．
　
5．解：由同位角相等两直线平行可知：①正确；由垂直于同一条直线的两条直线平行可知②、③正确；根据内错角相等两直线平行线可知④正确．
故选：D．
　
6．解：A、∠1、∠2是同旁内角，由∠1=∠2不能判定AB∥CD；
B、∠1、∠2是内错角，由∠1=∠2能判定AB∥CD；
C、∠1、∠2是内错角，由∠1=∠2能判定AC∥BD，不能判定AB∥CD；
D，∠1、∠2是同旁内角，由∠1=∠2不能判定AB∥CD；
故选B．
　
7．解：A、∵∠3=∠4，∴AD∥BC，故本选项正确；
B、∵∠1=∠2，∴AB∥CD，故本选项错误；
C、∵∠5=∠C，∴AB∥CD，故本选项错误；
D、∵∠1+∠3+∠A=180°，∴AB∥CD，故本选项错误．
故选A．
　
8．解：A、B、D若∠1=∠2，无法判定AB与CD的关系，故本选项错误；
C、若∠1=∠2，符合内错角相等，两直线平行，所以AB∥CD，故本选项正确．
故选C．
　
二．选择题（共13小题）
9．解：当∠2=50°时，a∥b；理由如下：
如图所示：
∵∠1=40°，
∴∠3=180°﹣90°﹣40°=50°，
当∠2=50°时，∠2=∠3，
∴a∥b；
故答案为：50．
　
10．解：∵OD∥AC，
∴∠BOD'=∠A=70°，
∴∠DOD'=78°﹣70°=8°．
故答案是：8°．
　
11．解：∵∠BAG=∠AHE=72°，∴AB∥EI；
∵∠BFC=∠FCD=72°，∴BG∥CD；
∵∠CBF=∠BGA=72°，∴BC∥AH；
∵∠EDI=∠CKD=72°，∴DE∥CF；
∵∠AEH=∠EID=72°，∴AE∥DK．
故共有5对平行线．
　
12．解：∵DF平分∠ADE，（已知）
∴∠EDF=∠ADE．（角平分线定义）
∵∠ADE=60°，（已知）
∴∠EDF=30°．（角平分线定义）
∵∠1=30°，（已知）
∴∠1=∠EDF，（等量代换）
∴DF∥BE，（内错角相等，两直线平行）；
故答案为：∠EDF，角平分线定义；∠EDF，角平分线定义；∠1=∠EDF，等量代换；DF∥BE，内错角相等，两直线平行．21世纪教育网版权所有
　
13．解：作CF∥AB，如图所示：
则∠ABC+∠1=180°，
∴∠1=180°﹣146°=34°，
∴∠2=∠BCD﹣∠1=60°﹣34°=26°，
∵∠2+∠EDC=26°+154°=180°，
∴CF∥ED，
∴AB∥ED；
故答案为：合格．
　
14解：①∵∠B+∠BCD=180°，
∴AB∥CD；
②∵∠1=∠2，
∴AD∥CB；
③∵∠3=∠4，
∴AB∥CD；
④∵∠B=∠5，
∴AB∥CD，
故答案为：①③④．
　
15．解：①∠DAC=∠ACB利用内错角相等两直线平行得到AD∥BC，错误；②∠BAC=∠ACD利用内错角相等两直线平行得到AB∥CD，正确；③∠BAD+∠ADC=180°利用同旁内角互补得到AB∥CD，正确；④∠BAD+∠ABC=180°利用同旁内角互补得到AD∥BC，错误；21教育网
故答案为：②③
　
16．解：①应为：两直线平行，同位角相等，故本小题错误；
②应为：在同一平面内，过一个点有且只有一条直线与已知直线垂直，故本小题错误；
③两直线相交成的四个角中相邻两角的角平分线互相垂直，故本小题正确；
④三条直线两两相交，总有一个交点或三个交点，故本小题错误；
⑤若a∥b，b∥c，则a∥c，故本小题正确；
⑥应为：在同一平面内，若a⊥b，b⊥c，则a⊥c，故本小题错误．
综上所述，正确的有③⑤．
故答案为③⑤．
　
17．解：如，延长EA交CD于M，
∵AB∥CD，
∴∠1=∠4，
∵∠4=∠1+∠3，
∴∠1=∠2+∠3．
故答案为∠1=∠2+∠3．
　
18 解：∵AB∥CD，
∴∠B+∠C=180°，
而∠C=60°，
∴∠B=120°，
而五边形的内角和为（5﹣2）×180°=540°，
∴∠E=540°﹣135°﹣60°﹣120°﹣150°=75°．
故答案为：75°．
　
19．解：∵AE∥DB，
∴∠1=∠3=3∠2，
∵∠2+∠C=∠3，
∴∠2+∠C=3∠2，
∴∠C=2∠2，
∵∠2=28°．
∴∠C=56°，
故答案为：56°．
　
20．解：∵AE∥BD，∠1=130°，∠2=30°，
∴∠CBD=∠1=130°．∠1+∠ABD=180°，
∴∠ABD=180°﹣∠1=180°﹣130°=50°，
∵∠BDC=∠2，
∴∠BDC=30°．
在△BCD中，∠CBD=130°，∠BDC=30°，
∴∠C=180°﹣130°﹣30°=20°，
故答案为：50°，20°．
　
三．解答题（共3小题）
21．解：OA∥BC，OB∥AC．
∵∠1=50°，∠2=50°，
∴∠1=∠2，
∴OB∥AC，
∵∠2=50°，∠3=130°，
∴∠2+∠3=180°，
∴OA∥BC．
　
22．解：（1）作法：①作射线AO；
②在射线AO上截取线段AC=30mm；
（2）作法：以C为顶点，利用量角器测得∠ACM=90°；
（3）作法：以A为顶点，利用量角器测得∠CAN=60°；
在直角三角形ABC中，∠CAB=60°，AC=30mm，
∴AB=AC÷cos∠CAB=60mm；
（4）作法：利用直尺，以A点为起点，量得AD=30mm，点D即为所求；
在直角三角形ABC中，CD为斜边AB上的中线，
∴CD=AB=30mm；
∴AB=2DC；
（5）作法：过点D作DE∥AC交CM于点E，DE即为所求；
∵DE⊥BC，AC⊥BC，
∵DE∥AC，
∴DE：AC=BD：AC=1：2，
∴DE=AC=15mm．
故答案为：（3）60；（4）30、2；（5）15、、平行．
　
23．解：∵EF∥AD，AD∥BC，
∴EF∥BC，
∴∠ACB+∠DAC=180°，
∵∠DAC=120°，
∴∠ACB=60°，
又∵∠ACF=20°，
∴∠FCB=∠ACB﹣∠ACF=40°，
∵CE平分∠BCF，
∴∠BCE=20°，
∵EF∥BC，
∴∠FEC=∠ECB，
∴∠FEC=20°．