1.4平行线的性质同步练习

浙教版七下数学1.4平行线的性质同步练习
　
一．选择题（共12小题）
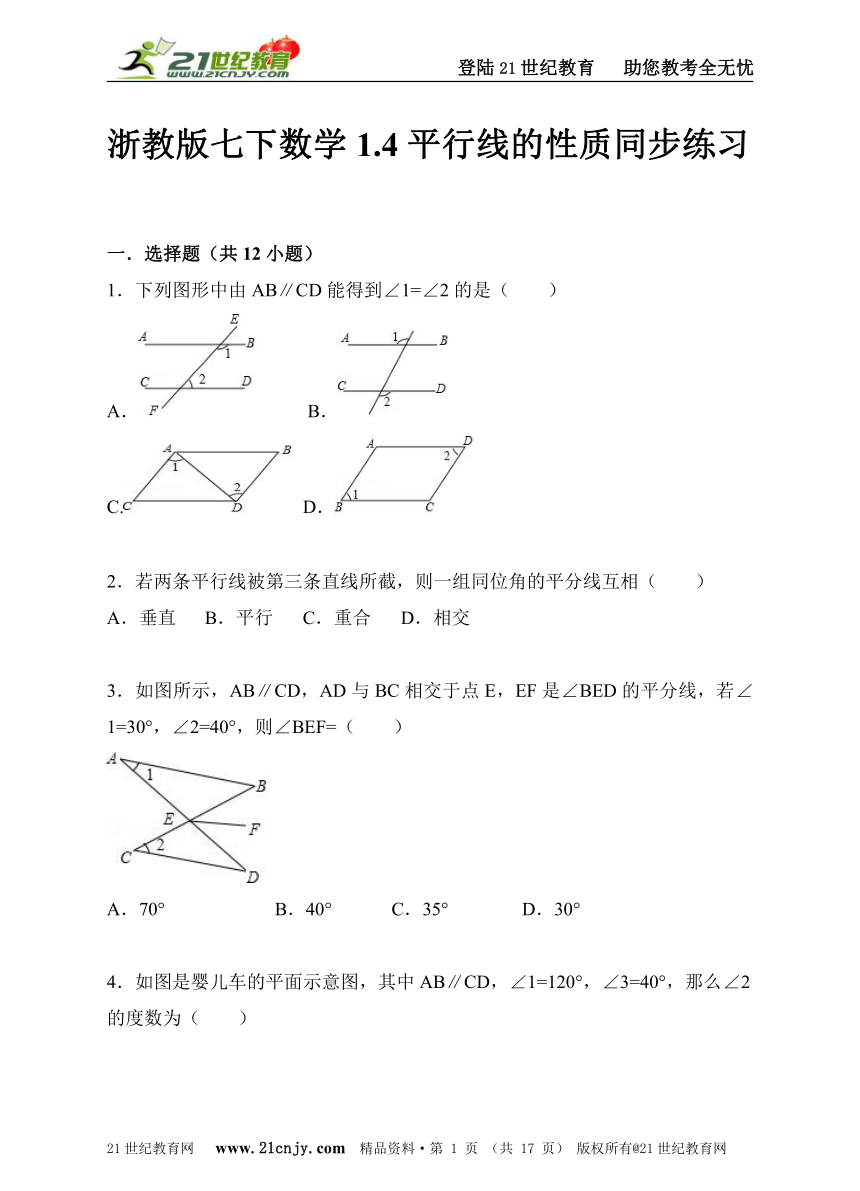
1．下列图形中由AB∥CD能得到∠1=∠2的是（　　）
A． B．
C. D．
2．若两条平行线被第三条直线所截，则一组同位角的平分线互相（　　）
A．垂直 B．平行 C．重合 D．相交
3．如图所示，AB∥CD，AD与BC相交于点E，EF是∠BED的平分线，若∠1=30°，∠2=40°，则∠BEF=（　　）www.21-cn-jy.com
A．70° B．40° C．35° D．30°
4．如图是婴儿车的平面示意图，其中AB∥CD，∠1=120°，∠3=40°，那么∠2的度数为（　　）2·1·c·n·j·y
A．80° B．90° C．100° D．102°
5．如图，将一副三角板叠放在一起，使直角的顶点重合于点O，AB∥OC，DC与OB交于点E，则∠DEO的度数为（　　）【来源：21·世纪·教育·网】
A．85° B．70° C．75° D．60°
6．如图，AB∥CD，∠B=68°，∠E=20°，则∠D的度数为（　　）
A．28° B．38° C．48° D．88°
7．若∠α与∠β的两边分别平行，且∠α=（x﹣10）°，∠β=（2x+25）°，则∠α的度数为（　　）21·世纪*教育网
A．45° B．55° C．45°或55° D．55°或65°
8．如图，直线AB∥CD，AE平分∠CAB．AE与CD相交于点E，∠ACD=40°，则∠BAE的度数是（　　）www-2-1-cnjy-com
A．40° B．70° C．80° D．140°
9．如图，直线a∥b，∠1=85°，∠2=35°，则∠3=（　　）
A．85° B．60° C．50° D．35°
10．如图，将一块直角三角板的直角顶点放在直尺的一边上．如果∠1=50°，那么∠2的度数是（　　）
A．30° B．40° C．50° D．60°
11．下列四个命题：①对顶角相等；②内错角相等；③平行于同一条直线的两条直线互相平行；④如果一个角的两边分别平行于另一个角的两边，那么这两个角相等．其中真命题的个数是（　　）21·cn·jy·com
A．1个 B．2个 C．3个 D．4个
12．如图，如果AB∥CD，那么下面说法错误的是（　　）
A．∠3=∠7 B．∠2=∠6
C．∠3+∠4+∠5+∠6=180° D．∠4=∠8
　
二．选择题（共6小题）
13．如图，根据图形填空
（1）∵∠A=　　（已知）∴AC∥DE（　　）
（2）∵∠2=　　（已知）∴DF∥AB（　　）
（3）∵∠2+∠6=180°（已知）∴　　∥　　（　　）
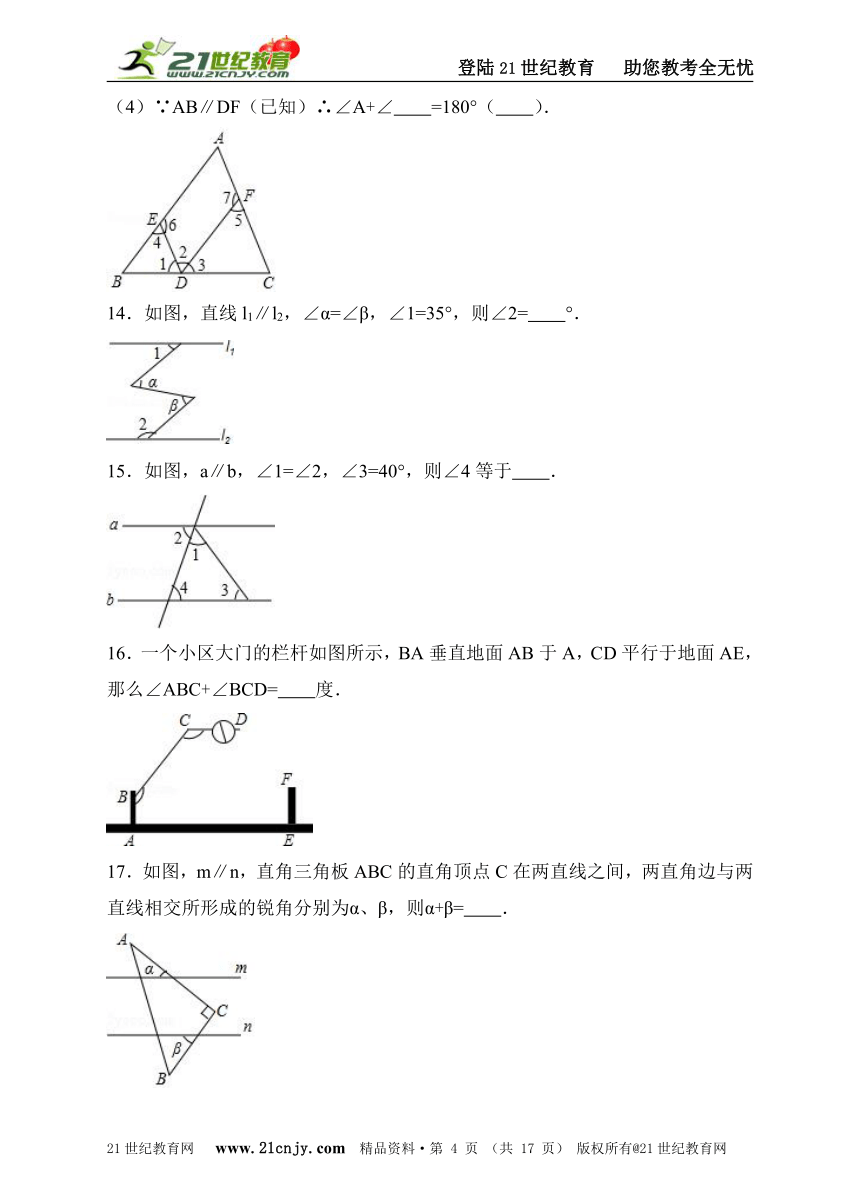
（4）∵AB∥DF（已知）∴∠A+∠　　=180°（　　）．
14．如图，直线l1∥l2，∠α=∠β，∠1=35°，则∠2=　　°．
15．如图，a∥b，∠1=∠2，∠3=40°，则∠4等于　　．
16．一个小区大门的栏杆如图所示，BA垂直地面AB于A，CD平行于地面AE，那么∠ABC+∠BCD=　　度．21*cnjy*com
17．如图，m∥n，直角三角板ABC的直角顶点C在两直线之间，两直角边与两直线相交所形成的锐角分别为α、β，则α+β=　　．【来源：21cnj*y.co*m】
　
三．选择题（共6小题）
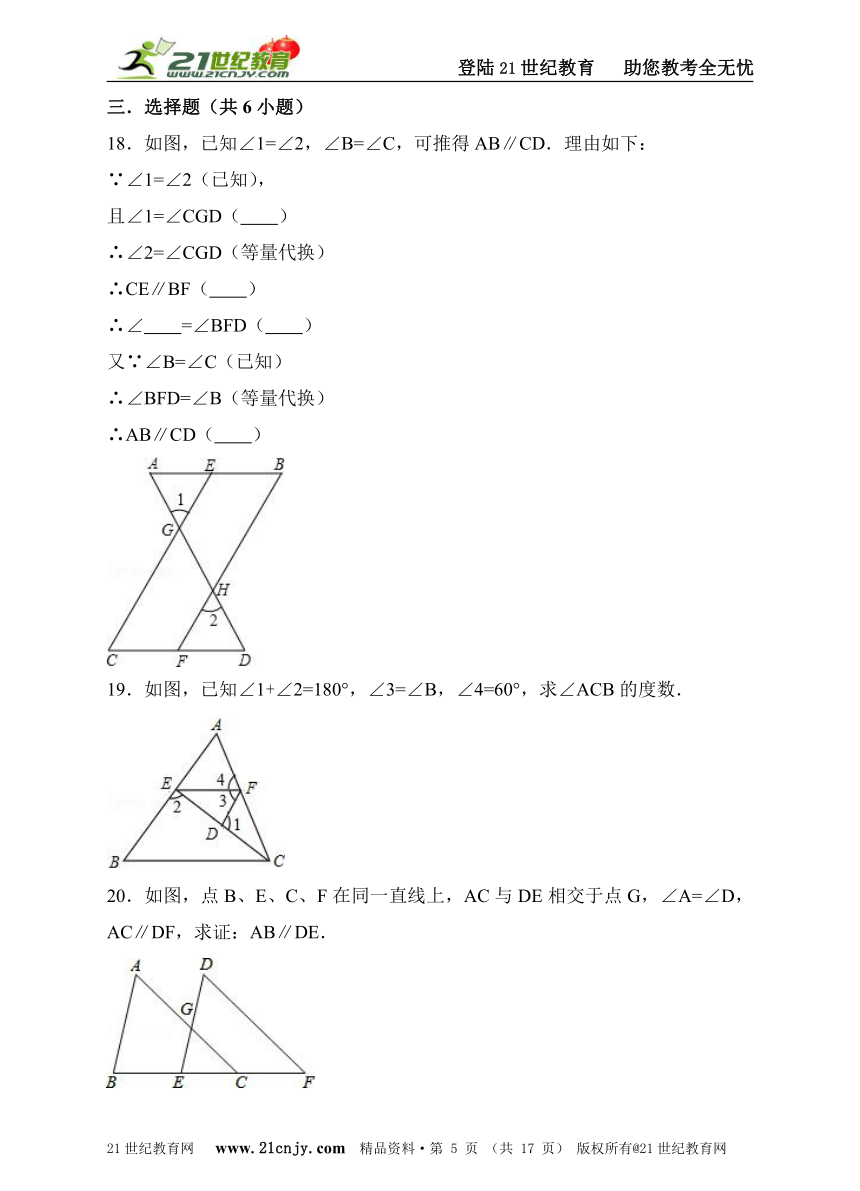
18．如图，已知∠1=∠2，∠B=∠C，可推得AB∥CD．理由如下：
∵∠1=∠2（已知），
且∠1=∠CGD（　　）
∴∠2=∠CGD（等量代换）
∴CE∥BF（　　）
∴∠　　=∠BFD（　　）
又∵∠B=∠C（已知）
∴∠BFD=∠B（等量代换）
∴AB∥CD（　　）
19．如图，已知∠1+∠2=180°，∠3=∠B，∠4=60°，求∠ACB的度数．
20．如图，点B、E、C、F在同一直线上，AC与DE相交于点G，∠A=∠D，AC∥DF，求证：AB∥DE．2-1-c-n-j-y
21．如图，已知ED∥AC，∠EDF=∠A，∠FDC=30°．求∠B的度数．
22．探索：小明和小亮在研究一个数学问题：已知AB∥CD，AB和CD都不经过点P，探索∠P与∠A，∠C的数量关系．【出处：21教育名师】
发现：在图1中，小明和小亮都发现：∠APC=∠A+∠C；
小明是这样证明的：过点P作PQ∥AB
∴∠APQ=∠A（　　）
∵PQ∥AB，AB∥CD．
∴PQ∥CD（　　）
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
小亮是这样证明的：过点作PQ∥AB∥CD．
∴∠APQ=∠A，∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
请在上面证明过程的过程的横线上，填写依据；两人的证明过程中，完全正确的是　　．
应用：
在图2中，若∠A=120°，∠C=140°，则∠P的度数为　　；
在图3中，若∠A=30°，∠C=70°，则∠P的度数为　　；
拓展：
在图4中，探索∠P与∠A，∠C的数量关系，并说明理由．
23．如图，已知直线l1∥l2，l3、l4和l1、l2分别交于点A、B、C、D，点P 在直线l3或l4上且不与点A、B、C、D重合．记∠AEP=∠1，∠PFB=∠2，∠EPF=∠3．21教育网
（1）若点P在图（1）位置时，求证：∠3=∠1+∠2；
（2）若点P在图（2）位置时，请直接写出∠1、∠2、∠3之间的关系；
（3）若点P在图（3）位置时，写出∠1、∠2、∠3之间的关系并给予证明．
　

浙教版七下数学1.4平行线的性质同步练习
参考答案与试题解析
　
一．选择题（共12小题）
1．解：A、∵AB∥CD，
∴∠1+∠2=180°，故本选项错误；
B、∵AB∥CD，
∴∠1=∠3，
又∵∠2=∠3，
∴∠1=∠2，故本选项正确；
C、根据AB∥CD可得∠BAD=∠CDA，不能推出∠1=∠2，故本选项错误；
D、根据AB∥CD不能推出∠1=∠2，故本选项错误；
故选B．
2．选B．
　
3．解：∵AB∥CD，
∴∠1=∠D，
∴∠BED=∠2+∠D=30°+40°=70°，
∵EF是∠BED的平分线，
∴∠BEF=∠BEF=35°，
故选：C．
4．解：∵AB∥CD，
∴∠A=∠3=40°，
∵∠1=120°，
∴∠2=∠1﹣∠A=80°，
故选A．
5．解：∵AB∥OC，∠A=60°，
∴∠A+∠AOC=180°，
∴∠AOC=120°，
∴∠BOC=120°﹣90°=30°，
∴∠DEO=∠C+∠BOC=45°+30°=75°；
故选：C．
　
6．解：如图，∵AB∥CD，
∴∠1=∠B=68°，
∵∠E=20°，
∴∠D=∠1﹣∠E=48°，
故选C．
　
7．解：∵∠α与∠β的两边分别平行，
∴∠α+∠β=180°或∠α=∠β，
∵∠α=（x﹣10）°，∠β=（2x+25）°，
∴x﹣10+2x+25=180或x﹣10=2x+25，
解得：x=55或﹣35（不合题意，舍去），
∴∠α=55°，
故选B
　
8．解：∵AB∥CD，
∴∠ACD+∠BAC=180°，
∵∠ACD=40°，
∴∠BAC=180°﹣40°=140°，
∵AE平分∠CAB，
∴∠BAE=∠BAC=×140°=70°，
故选B．
　
9．解：在△ABC中，
∵∠1=85°，∠2=35°，
∴∠4=85°﹣35°=50°，
∵a∥b，
∴∠3=∠4=50°，
故选C．
　
10．解：如图，
，
∵∠1=50°，
∴∠3=∠1=50°，
∴∠2=90°﹣50°=40°．
故选B．
　
11．解：①符合对顶角的性质，故本小题正确；
②两直线平行，内错角相等，故本小题错误；
③符合平行线的判定定理，故本小题正确；
④如果一个角的两边分别平行于另一个角的两边，那么这两个角相等或互补，故本小题错误．
故选B．
　
12．解：∵AB∥CD，
∴∠3=∠7，∠2=∠6，∠3+∠4+∠5+∠6=180°．
故选D．
　
二．选择题（共6小题）
13．解：（1）∵∠A=∠4（已知）
∴AC∥DE（同位角相等，两直线平行）
（2）∵∠2=∠4（已知）
∴DF∥AB（内错角相等，两直线平行）
（3）∵∠2+∠6=180°（已知）
∴AB∥DF（同旁内角互补，两直线平行）
（4）∵AB∥DF（已知）
∴∠A+∠7=180°（两直线平行，同旁内角互补）．
故答案为：（1）∠4；同位角相等，两直线平行；（2）∠4；内错角相等，两直线平行；（3）AB，DF，同旁内角互补，两直线平行；（4）7；两直线平行，同旁内角互补．21世纪教育网版权所有
　
14．解：如图，
∵l1∥l2，
∴∠3=∠1=35°，
∵∠α=∠β，
∴AB∥CD，
∴∠2+∠3=180°，
∴∠2=180°﹣∠3=180°﹣135°=145°．
故答案为145°．
　
15．解：∵a∥b，∠3=40°，
∴∠1+∠2=180°﹣40°=140°，∠2=∠4，
∵∠1=∠2，
∴∠2=70°，
∴∠4=∠2=70°．
故答案为：70°．
　
16．解：作CH⊥AE于H，如图，
∵AB⊥AE，CH⊥AE，
∴AB∥CH，
∴∠ABC+∠BCH=180°，
∵CD∥AE，
∴∠DCH+∠CHE=180°，
而∠CHE=90°，
∴∠DCH=90°，
∴∠ABC+∠BCD=180°+90°=270°．
故答案为270．
　
17．解：过C作CE∥m，
∵m∥n，
∴CE∥n，
∴∠1=∠α，∠2=∠β，
∵∠1+∠2=90°，
∴∠α+∠β=90°，
故答案为：90°．
　
三．选择题（共6小题）
18．解：∵∠1=∠2（已知），
且∠1=∠CGD（对顶角相等），
∴∠2=∠CGD（等量代换），
∴CE∥BF（同位角相等，两直线平行），
∴∠C=∠BFD（两直线平行，同位角相等），
又∵∠B=∠C（已知），
∴∠BFD=∠B（等量代换），
∴AB∥CD（内错角相等，两直线平行）．
故答案为：（对顶角相等），（同位角相等，两直线平行），C，（两直线平行，同位角相等），（内错角相等，两直线平行）．21cnjy.com
　
19．解：∵∠1+∠2=180°，∠AEC+∠2=180°，
∴∠1=∠AEC，
∴AB∥DF，
∴∠AEF=∠3，
∵∠3=∠B，
∴∠AEF=∠B，
∴EF∥BC，
∴∠ACB=∠4=60°．
　
20．证明：∵AC∥DF，
∴∠D=∠EGC，
又∵∠A=∠D，
∴∠A=∠EGC，
∴AB∥DE．
　
21．解：∵ED∥AC，
∴∠BED=∠A，
∵∠EDF=∠A，
∴∠BED=∠EDF，
∴AB∥DF，
∴∠B=∠FDC=30°．
　
22．解：如图1，过点P作PQ∥AB，
∴∠APQ=∠A（两直线平行，内错角相等）
∵PQ∥AB，AB∥CD．
∴PQ∥CD（平行于同一直线的两直线平行）
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C，
故两人的证明过程中，完全正确的是小明的证法；
如图2，过点P作PE∥AB，
∴∠APE+∠A=180°，∠A=120°，∴∠APE=60°，
∵PE∥AB，AB∥CD．
∴PE∥CD（平行于同一直线的两直线平行）
∴∠CPE+∠C=180°，∠C=140°，∴∠CPE=40°，
∴∠APC=∠APE+∠CPE
=100°；
如图3，过点P作PF∥AB，
∴∠APF=∠A，
∵PF∥AB，AB∥CD．
∴PF∥CD，
∴∠CPF=∠C
∴∠CPF﹣∠APF=∠C﹣∠A
即∠APC=∠C﹣∠A=40°；
如图4，过点P作PG∥AB，
∴∠APG+∠A=180°，∴∠APG=180°﹣∠A
∵PG∥AB，AB∥CD，
∴PG∥CD，（平行于同一直线的两直线平行）
∴∠CPG+∠C=180°，∴∠CPG=180°﹣∠C
∴∠APC=∠CPG﹣∠APG=∠A﹣∠C．
　
23．证明：（1）过P作PQ∥l1∥l2，
由两直线平行，内错角相等，可得：
∠1=∠QPE、∠2=∠QPF；
∵∠3=∠QPE+∠QPF，
∴∠3=∠1+∠2．
（2）关系：∠3=∠2﹣∠1；
过P作直线PQ∥l1∥l2，
则：∠1=∠QPE、∠2=∠QPF；
∵∠3=∠QPF﹣∠QPE，
∴∠3=∠2﹣∠1．
（3）关系：∠3=360°﹣∠1﹣∠2．
过P作PQ∥l1∥l2；
同（1）可证得：∠3=∠CEP+∠DFP；
∵∠CEP+∠1=180°，∠DFP+∠2=180°，
∴∠CEP+∠DFP+∠1+∠2=360°，
即∠3=360°﹣∠1﹣∠2．