1.5平移同步练习

浙教版七下数学1.5平移同步练习
　
一．选择题（共9小题）
1．下列生活中的现象，属于平移的是（　　）
A．升降电梯从底楼升到顶楼 B．闹钟的钟摆的运动
C．DVD片在光驱中运行 D．秋天的树叶从树上随风飘落
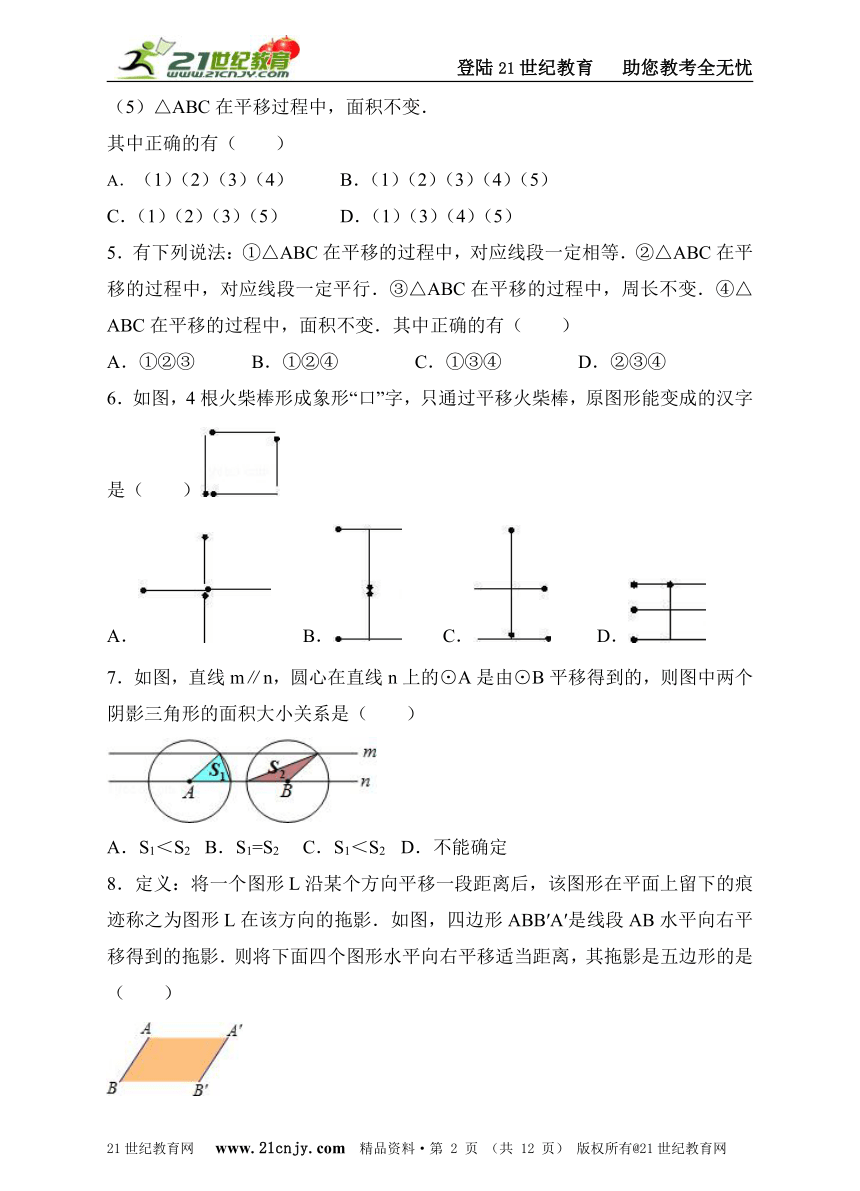
2．如图，将周长为4的△ABC沿BC方向向右平移1个单位得到△DEF，则四边形ABFD的周长为（　　）21世纪教育网版权所有

A．5 B．6 C．7 D．8
3．如图，在6×6方格中有两个涂有阴影的图形M、N，①中的图形M平移后位置如②所示，以下对图形M的平移方法叙述正确的是（　　）
A．向右平移2个单位，向下平移3个单位
B．向右平移1个单位，向下平移3个单位
C．向右平移1个单位，向下平移4个单位
D．向右平移2个单位，向下平移4个单位
4．在下列说法中：
（1）△ABC在平移过程中，对应线段一定相等
（2）△ABC在平移过程中，对应线段一定平行
（3）△ABC在平移过程中，周长保持不变
（4）△ABC在平移过程中，对应边中点的连线段的长等于平移的距离
（5）△ABC在平移过程中，面积不变．
其中正确的有（　　）
（1）（2）（3）（4） B．（1）（2）（3）（4）（5）
C．（1）（2）（3）（5） D．（1）（3）（4）（5）
5．有下列说法：①△ABC在平移的过程中，对应线段一定相等．②△ABC在平移的过程中，对应线段一定平行．③△ABC在平移的过程中，周长不变．④△ABC在平移的过程中，面积不变．其中正确的有（　　）21教育网
A．①②③ B．①②④ C．①③④ D．②③④
6．如图，4根火柴棒形成象形“口”字，只通过平移火柴棒，原图形能变成的汉字是（　　）
A． B． C． D．
7．如图，直线m∥n，圆心在直线n上的⊙A是由⊙B平移得到的，则图中两个阴影三角形的面积大小关系是（　　）21cnjy.com
A．S1＜S2 B．S1=S2 C．S1＜S2 D．不能确定
8．定义：将一个图形L沿某个方向平移一段距离后，该图形在平面上留下的痕迹称之为图形L在该方向的拖影．如图，四边形ABB′A′是线段AB水平向右平移得到的拖影．则将下面四个图形水平向右平移适当距离，其拖影是五边形的是（　　）2·1·c·n·j·y
A． B． C． D．
9．如图，两个全等的直角三角形重叠在一起，将Rt△ABC沿着BC的方向平移到Rt△DEF的位置，已知AB=5，DO=2，平移距离为3，则阴影部分的面积为（　　）【来源：21·世纪·教育·网】
A．12 B．24 C．21 D．20.5
　
二．填空题（共4小题）
10．如图，把三角板的斜边紧靠直尺平移，一个顶点从刻度“5”平移到刻度“10”，则顶点C平移的距离CC′=　　．www.21-cn-jy.com
11．如图，△ABC中，AB=AC，BC=12cm，点D在AC上，DC=4cm．将线段DC沿着CB的方向平移7cm得到线段EF，点E，F分别落在边AB，BC上，则△EBF的周长为　　cm．21·世纪*教育网
12．某景点拟在如图的矩形荷塘上架设小桥，若荷塘中小桥的总长为100米，则荷塘周长为　　．
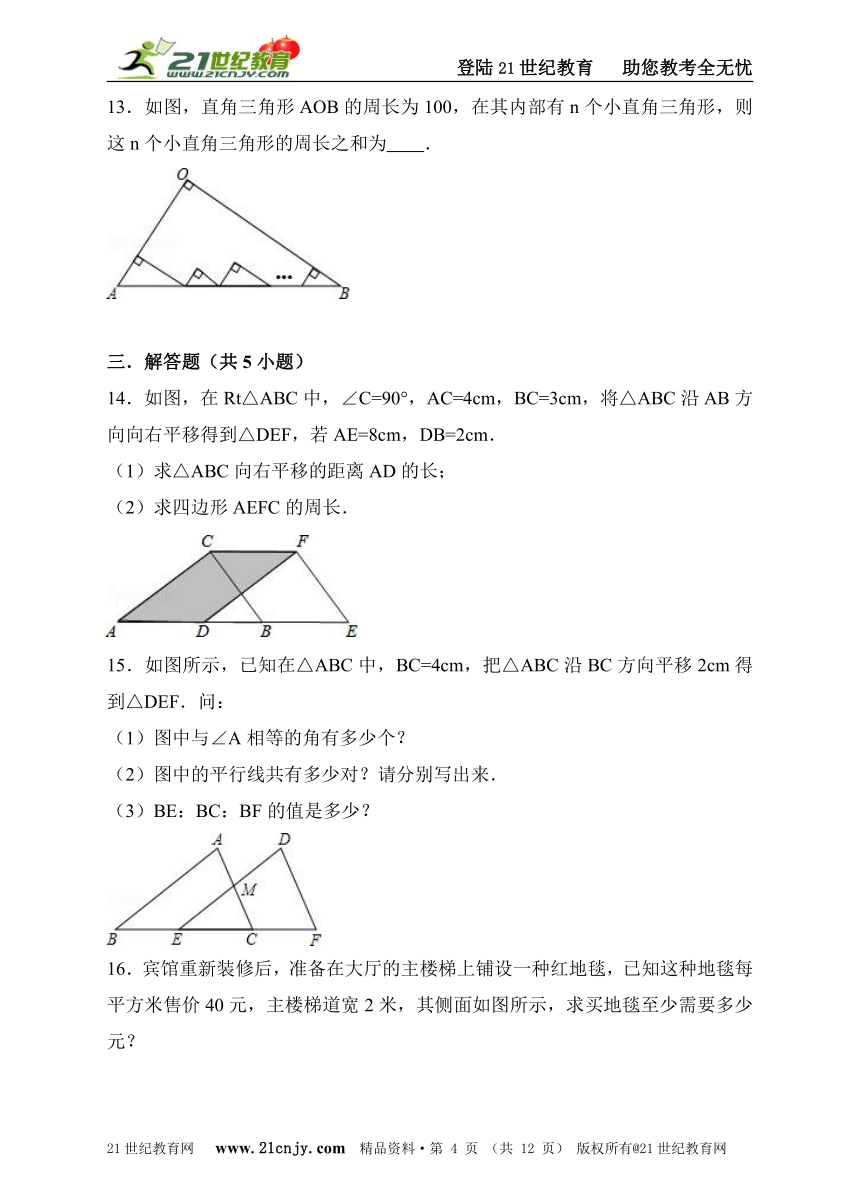
13．如图，直角三角形AOB的周长为100，在其内部有n个小直角三角形，则这n个小直角三角形的周长之和为　　．www-2-1-cnjy-com
　
三．解答题（共5小题）
14．如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=3cm，将△ABC沿AB方向向右平移得到△DEF，若AE=8cm，DB=2cm．21·cn·jy·com
（1）求△ABC向右平移的距离AD的长；
（2）求四边形AEFC的周长．
15．如图所示，已知在△ABC中，BC=4cm，把△ABC沿BC方向平移2cm得到△DEF．问：
（1）图中与∠A相等的角有多少个？
（2）图中的平行线共有多少对？请分别写出来．
（3）BE：BC：BF的值是多少？
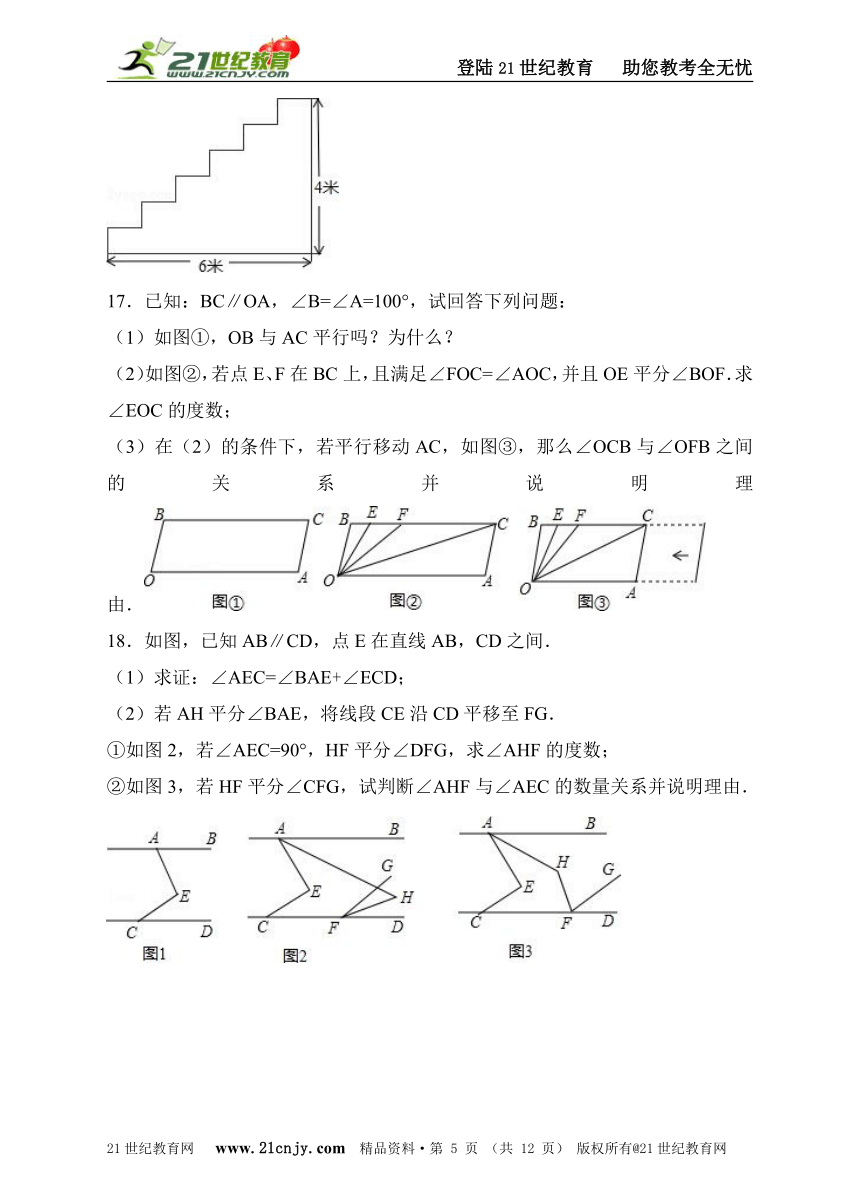
16．宾馆重新装修后，准备在大厅的主楼梯上铺设一种红地毯，已知这种地毯每平方米售价40元，主楼梯道宽2米，其侧面如图所示，求买地毯至少需要多少元？2-1-c-n-j-y
17．已知：BC∥OA，∠B=∠A=100°，试回答下列问题：
（1）如图①，OB与AC平行吗？为什么？
（2）如图②，若点E、F在BC上，且满足∠FOC=∠AOC，并且OE平分∠BOF．求∠EOC的度数；21*cnjy*com
（3）在（2）的条件下，若平行移动AC，如图③，那么∠OCB与∠OFB之间的关系并说明理由．
18．如图，已知AB∥CD，点E在直线AB，CD之间．
（1）求证：∠AEC=∠BAE+∠ECD；
（2）若AH平分∠BAE，将线段CE沿CD平移至FG．
①如图2，若∠AEC=90°，HF平分∠DFG，求∠AHF的度数；
②如图3，若HF平分∠CFG，试判断∠AHF与∠AEC的数量关系并说明理由．
　

浙教版七下数学1.5平移同步练习
参考答案与试题解析
　
一．选择题（共9小题）
1．解：A、升降电梯从底楼升到顶楼，符合平移的性质，故属于平移；
B、闹钟的钟摆的运动，运动过程中改变了方向，不符合平移的性质；
C、DVD片在光驱中运行，运动过程中改变了方向，不符合平移的性质；
D、秋天的树叶从树上随风飘落，运动过程中改变了方向，不符合平移的性质．
故选A．
　
2．解：∵△ABC沿BC方向向右平移1个单位得到△DEF，
∴DF=AC，AD=CF=1，
∴四边形ABFD的周长=AB+BF+DF+AD=AB+BC+CF+AC+AD
=△ABC的周长+CF+AD=4+1+1=6．
故选B．
　
3．解：根据图形M平移前后对应点的位置变化可知，需要向右平移1个单位，向下平移3个单位．
故选（B）
　
4．解：（1）△ABC在平移的过程中，对应线段一定相等，正确；
（2）△ABC在平移过程中，对应线段一定平行或在同一直线上，故本小题错误；
（3）△ABC在平移过程中，周长保持不变，正确；
（4）△ABC在平移过程中，对应边中点的连线的长度等于平移的距离，正确．
（5）△ABC在平移过程中，面积不变，正确．
综上所述，正确的（1）（3）（4）（5）．
故选D．
　
5．解：①∵平移不改变图形的大小，∴△ABC在平移过程中，对应线段一定相等，故正确；
②∵经过平移，对应线段所在的直线共线或平行，∴对应线段一定平行错误；
③∵平移不改变图形的形状和大小，∴△ABC在平移过程中，周长不变，故正确；
④∵平移不改变图形的大小和形状，∴△ABC在平移过程中，面积不变，正确；
∴①、③、④都符合平移的基本性质，都正确．
故选C．
　
6．解：观察可知，平移后的图形，上下火柴棒方向不变，位置改变；左右火柴棒，往中间移动，方向不变，位置改变．只有B符合．【来源：21cnj*y.co*m】
故选B．
　
7．解：∵圆心在直线n上的⊙A是由⊙B平移得到的，
∴两圆的半径相等，
∴图中两个阴影三角形等底等高，
∴两圆的面积相等，
故选B．
　
8．解：只有三角形的拖影是五边形，
故选A
　
9．解：∵△ABC沿BCC的方向平移到△DEF的位置，
∴S△ABC=S△DEF，
∴S阴影部分+S△OEC=S梯形ABEO+S△OEC，
∴S阴影部分=S梯形ABEO=×（5﹣2+5）×3=12．
故选：A．
　
二．填空题（共4小题）
10．解：∵把三角板的斜边紧靠直尺平移，一个顶点从刻度“5”平移到刻度“10”，
∴三角板向右平移了5个单位，
∴顶点C平移的距离CC′=5．
故答案为：5．
　
11．解：∵将线段DC沿着CB的方向平移7cm得到线段EF，
∴EF=DC=4cm，FC=7cm，
∵AB=AC，BC=12cm，
∴∠B=∠C，BF=5cm，
∴∠B=∠BFE，
∴BE=EF=4cm，
∴△EBF的周长为：4+4+5=13（cm）．
故答案为：13．
　
12．解：∵荷塘中小桥的总长为100米，
∴荷塘周长为：2×100=200（m）
故答案为：200m．
　
13．解：如图所示：过小直角三角形的直角定点作AO，BO的平行线，
所得四边形都是矩形．
则小直角三角形的与AO平行的边的和等于AO，与BO平行的边的和等于BO．
因此小直角三角形的周长等于直角△ABC的周长．
故这n个小直角三角形的周长为100．
故答案为：100．
　
三．解答题（共5小题）
14．解：（1）∵△ABC沿AB方向向右平移得到△DEF，
∴AD=BE=CF，BC=EF=3cm，
∵AE=8cm，DB=2cm，
∴AD=BE=CF==3cm；
（2）四边形AEFC的周长=AE+EF+CF+AC=8+3+3+4=18cm．
　
15．解：（1）有3个，分别是∠D，∠EMC，∠AMD．
（2）两对，AB∥DE，AC∥DF．
（3）∵△ABC沿BC方向平移2cm，
∴BE=CF=2cm．
又∵BC=4cm，
∴BF=6cm．
∴BE：BC：BF=1：2：3．
　
16．解：如图，利用平移线段，把楼梯的横竖向上向左平移，构成一个矩形，长宽分别为6米，4米，
∴地毯的长度为6+4=10米，地毯的面积为10×2=20平方米，
∴买地毯至少需要20×40=800元．
　
17．解（1）证明：∵BC∥OA，
∴∠B+∠O=180°，
∴∠O=180°﹣∠B=80°，
而∠A=100°，
∴∠A+∠O=180°，
∴OB∥AC；
（2）∵OE平分∠BOF，
∴∠BOE=∠FOE，
而∠FOC=∠AOC，
∴∠EOF+∠COF=∠AOB=×80°=40°；
（3）结论为：∠OFB=2∠OCB；
∵BC∥OA，
∴∠OCB=∠AOC，∠OFB=∠AOF，
∵∠FOC=∠AOC，
∴∠AOF=2∠AOC，
∴∠OFB=2∠OCB．
　
18．解：（1）如图1，过点E作直线EN∥AB，
∵AB∥CD，
∴EN∥CD，
∴∠BAE=∠AEN，∠DCE=∠CEN，
∴∠AEC=∠AEN+∠CEN=∠BAH+∠ECD；
（2）∵AH平分∠BAE，
∴∠BAH=∠EAH，
①∵HF平分∠DFG，设∠GFH=∠DFH=x，
又CE∥FG，
∴∠ECD=∠GFD=2x，
又∠AEC=∠BAE+∠ECD，∠AEC=90°，
∴∠BAH=∠EAH=45°﹣x，
如图2，过点H作l∥AB，
易证∠AHF=∠BAH+∠DFH=45°﹣x+x=45°；
②设∠GFD=2x，∠BAH=∠EAH=y，
∵HF平分∠CFG，
∴∠GFH=∠CFH=90°﹣x，
由（1）知∠AEC=∠BAE+∠ECD=2x+2y，
如图3，过点H作l∥AB，
易证∠AHF﹣y+∠CFH=180°，
即∠AHF﹣y+90°﹣x=180°，∠AHF=90°+（x+y），
∴∠AHF=90°+∠AEC．（或2∠AHF﹣∠AEC=180°．）