1.3平行线的判定(1) 同步练习

登陆21世纪教育 助您教考全无忧
平行线的判定
班级：___________姓名：___________得分：__________
一．选择题(每小题5分，共35分)
1．已知：如图所示，∠1=∠B，则下列说法正确的是（　　）
A．AB与CD平行 B．AC与DE平行
C．AB与CD平行，AC与DE也平行 D．以上说法都不正确
2．在同一平面内，如果l1∥l2、l2⊥l3，则l1与l3的位置关系（　　）
A．相交 B．垂直 C．平行 D．以上全不对
3．a、b、c、d为互不重合的四条直线，则下列推理中正确的是（　　）
A．因为a∥b，b∥c，所以d∥c B．因为a∥d，b∥c，所以d∥c
C．因为a∥d，b∥d，所以a∥b D．因为a∥d，a∥b，所以c∥d
4．下列说法正确的是（　　）
A．同位角相等
B．和已知直线平行的直线有且只有一条
C．在平面内过一点有且只有一条直线垂直于已知直线
D．在平面内过一点有且只有一条直线平行于已知直线
5．同一平面内有三条直线a，b，c，若a⊥b．b⊥c，则a与c（　　）
A．平行 B．垂直 C．平行或垂直 D．平行或重合
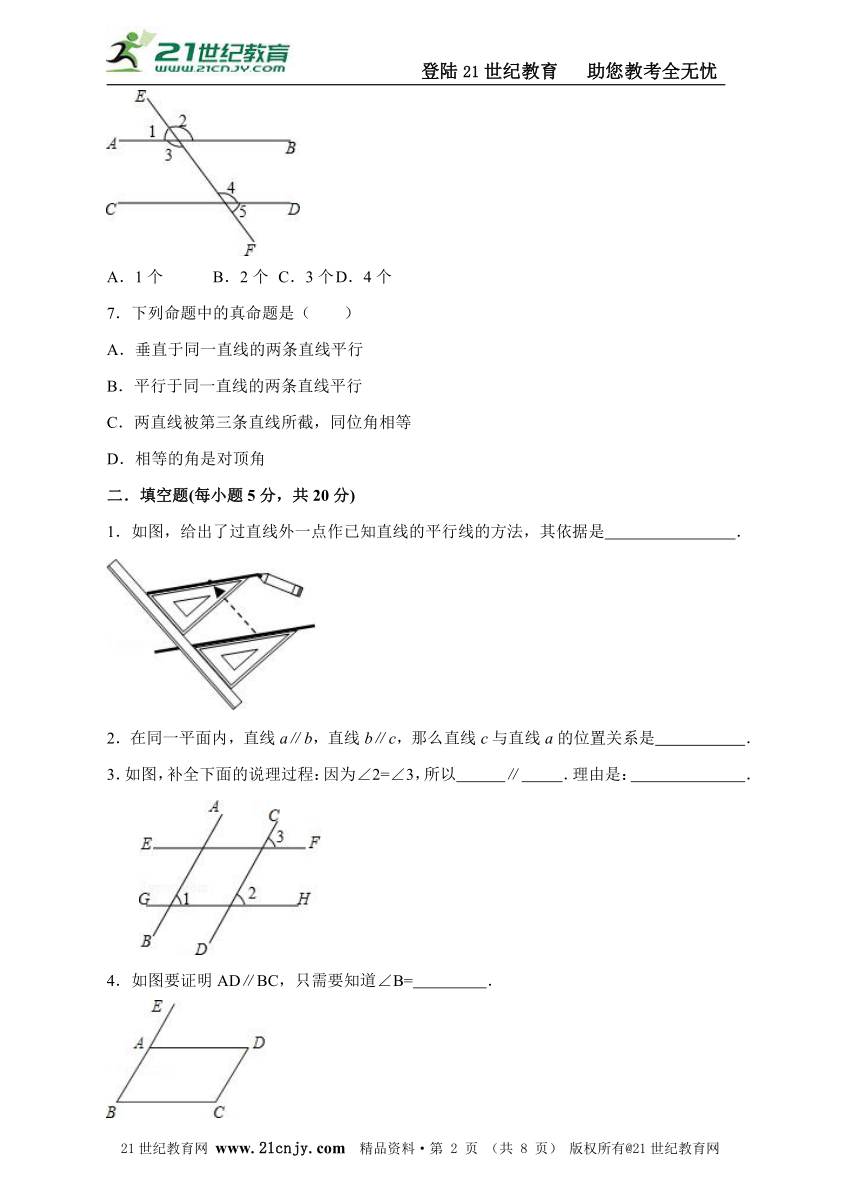
6．如图，已知∠1=30°，下列结论正确的有（　　）
①若∠2=30°，则AB∥CD
②若∠5=30°，则AB∥CD
③若∠3=150°，则AB∥CD
④若∠4=150°，则AB∥CD．
A．1个 B．2个 C．3个 D．4个
7．下列命题中的真命题是（　　）
A．垂直于同一直线的两条直线平行
B．平行于同一直线的两条直线平行
C．两直线被第三条直线所截，同位角相等
D．相等的角是对顶角
二．填空题(每小题5分，共20分)
1．如图，给出了过直线外一点作已知直线的平行线的方法，其依据是　 　．
2．在同一平面内，直线a∥b，直线b∥c，那么直线c与直线a的位置关系是　 　．
3．如图，补全下面的说理过程：因为∠2=∠3，所以　 　∥　 　．理由是：　 　．
4．如图要证明AD∥BC，只需要知道∠B=　 　．
三．解答题(每小题15分，共45分)
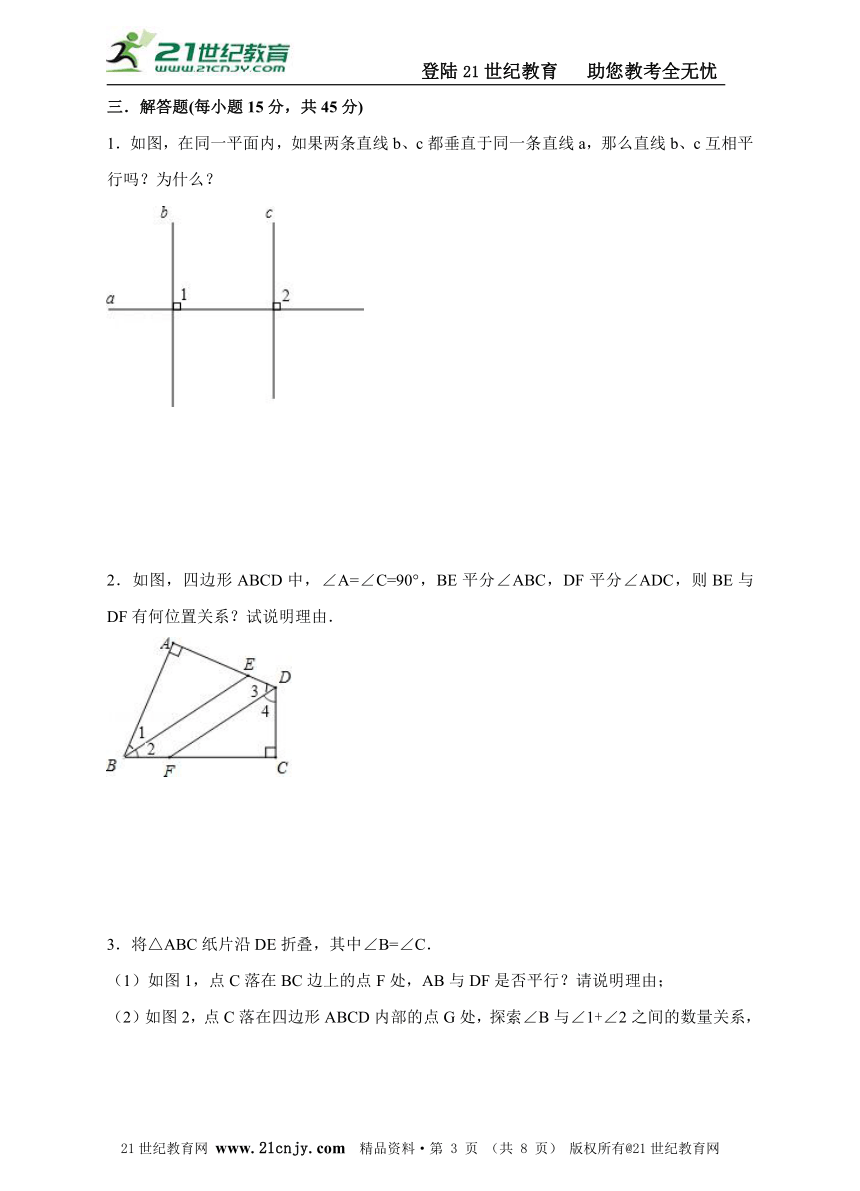
1．如图，在同一平面内，如果两条直线b、c都垂直于同一条直线a，那么直线b、c互相平行吗？为什么？
2．如图，四边形ABCD中，∠A=∠C=90°，BE平分∠ABC，DF平分∠ADC，则BE与DF有何位置关系？试说明理由．21世纪教育网版权所有
3．将△ABC纸片沿DE折叠，其中∠B=∠C．
（1）如图1，点C落在BC边上的点F处，AB与DF是否平行？请说明理由；
（2）如图2，点C落在四边形ABCD内部的点G处，探索∠B与∠1+∠2之间的数量关系，并说明理由．
参考答案
一．选择题(每小题5分，共35分)
1．A
【解析】∵∠1=∠B，∴AB∥CD（同位角相等，两直线平行）．
故选A．
2．B
【解析】∵l1∥l2，l2⊥l3，
∴l1⊥l3．
故选：B．
3．C
【解析】A、应为：因为a∥b，b∥c，所以a∥c，故本选项错误；
B、由a∥d，b∥c无法得到d∥c，故本选项错误；
C、因为a∥d，b∥d，所以a∥b正确，故本选项正确；
D、应为：因为a∥d，a∥b，所以b∥d，故本选项错误．
故选C．
4．C
【解析】A、两直线平行，同位角相等，故错误；
B、平面内和已知直线平行的直线有且只有一条，故错误；
C、在平面内过一点有且只有一条直线垂直于已知直线，正确；
D、在平面内过直线外一点有且只有一条直线平行于已知直线，故错误，
故选C．
5．A
【解答】如图，∵a⊥b，b⊥c，
∴a∥c．
故选A．
6．B
【解析】∵∠1=30°，∴∠2=150°，∴①错误；
∵∠4=150°，
∴∠2=∠4，
∴AB∥CD（同位角相等，两直线平行），∴④正确；
∵∠1=30°，
∴∠3=150°，
∵∠5=30°，
∴∠4=150°，
∴∠3=∠4，
∴AB∥CD（内错角相等，两直线平行），∴②正确；
根据∠1=30°，∠3=150°不能推出AB∥CD，∴③错误；
即正确的个数是2个，
故选B．
7．B
【解析】A、必须强调在同一平面内，故A错误；
B、符合平行公理，正确；
C、必须是两平行的直线被第三条直线所截，同位角才相等，所以C错误；
D、对顶角相等，但相等的角不一定是对顶角，所以D错误；
正确的是B．
故选B．
二．填空题(每小题5分，共20分)
1．同位角相等，两直线平行．
【解析】由图形得，有两个相等的同位角，所以只能依据：同位角相等，两直线平行．
2．a∥c．
【解析】∵在同一平面内，直线a∥b，直线b∥c，
∴直线c与直线a的位置关系是：a∥c．
故答案为：a∥c．
3．EF；GH；同位角相等，两直线平行
【解析】因为∠2=∠3，所以EF∥GH．理由是：同位角相等，两直线平行．
故答案为EF；GH；同位角相等，两直线平行．
4．∠EAD．
【解析】∠B=∠EAD，
理由是：∵∠B=∠EAD，
∴AD∥BC（同位角相等，两直线平行），
故答案为：∠EAD．
三．解答题(每小题15分，共45分)
1．答案见解析．
【解析】∵b⊥a，c⊥a，
∴b∥c；
因为：如果两条直线都与第三条直线垂直，那么这两条直线互相平行．
2．答案见解析．
【解析】BE∥DF．理由如下：
∵∠A=∠C=90°（已知），
∴∠ABC+∠ADC=180°（四边形的内角和等于360°）．
∵BE平分∠ABC，DF平分∠ADC，
∴∠1=∠2=∠ABC，∠3=∠4=∠ADC（角平分线的定义）．
∴∠1+∠3=（∠ABC+∠ADC）=×180°=90°（等式的性质）．
又∠1+∠AEB=90°（三角形的内角和等于180°），
∴∠3=∠AEB（同角的余角相等）．
∴BE∥DF（同位角相等，两直线平行）．
3．答案见解析．
【解析】（1）AB与DF平行．理由如下：
由翻折，得∠DFC=∠C．
又∵∠B=∠C，
∴∠B=∠DFC，
∴AB∥DF．
（2）连接GC，如图所示．
由翻折，得∠DGE=∠ACB．
∵∠1=∠DGC+∠DCG，∠2=∠EGC+∠ECG，
∴∠1+∠2=∠DGC+∠DCG+∠EGC+∠ECG=（∠DGC+∠EGC）+（∠DCG+∠ECG）=∠DGE+∠DCE=2∠ACB．21教育网
∵∠B=∠ACB，
∴∠1+∠2=2∠B．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网 www.21cnjy.com 精品资料·第 8 页 （共 8 页） 版权所有@21世纪教育网