1.3平行线的判定(2) 同步练习

平行线的判定
班级：___________姓名：___________得分：__________
一．选择题(每小题5分，共35分)
1．如图，下列条件中不能判定AB∥CD的是（　　）
A．∠3=∠4 B．∠1=∠5 C．∠1+∠4=180° D．∠3=∠5
2．如图，能判定EC∥AB的条件是（　　）
A．∠B=∠ACE B．∠A=∠ECD C．∠B=∠ACB D．∠A=∠ACE
3．如图，四边形纸片ABCD，以下测量方法，能判定AD∥BC的是（　　）
A．∠B=∠C=90° B．∠B=∠D=90°
C．AC=BD D．点A， D到BC的距离相等
4．如图，在四边形ABCD中，若∠1=∠2，则AD∥BC，理由是（　　）
A．两直线平行，内错角相等 B．两直线平行，同位角相等
C．内错角相等，两直线平行 D．同位角相等，两直线平行
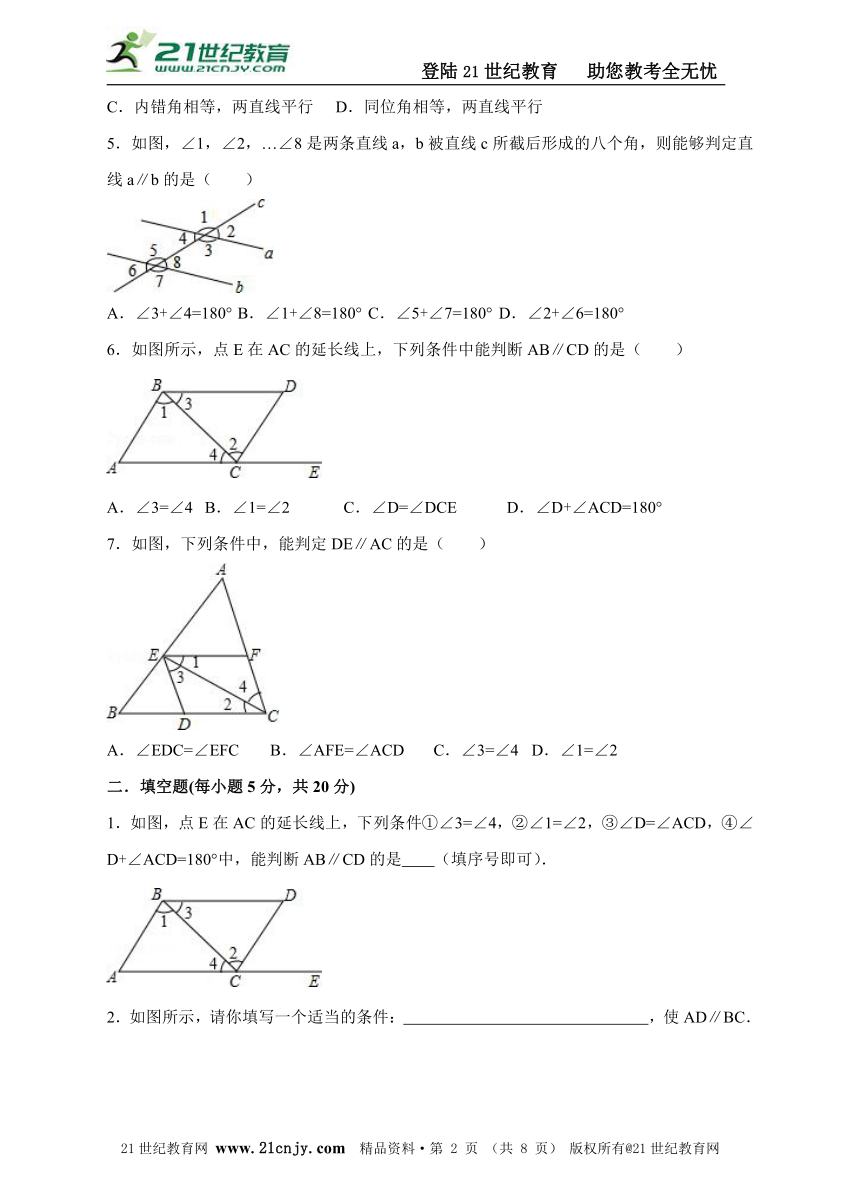
5．如图，∠1，∠2，…∠8是两条直线a，b被直线c所截后形成的八个角，则能够判定直线a∥b的是（　　）21世纪教育网版权所有
A．∠3+∠4=180° B．∠1+∠8=180° C．∠5+∠7=180° D．∠2+∠6=180°
6．如图所示，点E在AC的延长线上，下列条件中能判断AB∥CD的是（　　）
A．∠3=∠4 B．∠1=∠2 C．∠D=∠DCE D．∠D+∠ACD=180°
7．如图，下列条件中，能判定DE∥AC的是（　　）
A．∠EDC=∠EFC B．∠AFE=∠ACD C．∠3=∠4 D．∠1=∠2
二．填空题(每小题5分，共20分)
1．如图，点E在AC的延长线上，下列条件①∠3=∠4，②∠1=∠2，③∠D=∠ACD，④∠D+∠ACD=180°中，能判断AB∥CD的是　　（填序号即可）．21cnjy.com
2．如图所示，请你填写一个适当的条件：　 　，使AD∥BC．
3．如图，是小明学习三线八角时制作的模具，经测量∠2=100°，要使木条a与b平行，则∠1的度数必须是　 　．21·cn·jy·com
4．如图，∵　 　 （己知）
∴BC∥AD（内错角相等，两直线平行）
三．解答题(每小题15分，共45分)
1．将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起（其中，∠A=60°，∠D=30°；∠E=∠B=45°）：www.21-cn-jy.com
（1）①若∠DCE=45°，则∠ACB的度数为　 　；
②若∠ACB=140°，求∠DCE的度数；
（2）由（1）猜想∠ACB与∠DCE的数量关系，并说明理由．
2．已知∠1+∠2=90°，即∠BED=90°；那么∠3+∠FDE=90°，将等角代换，即可得出∠3与∠2的数量关系．2·1·c·n·j·y
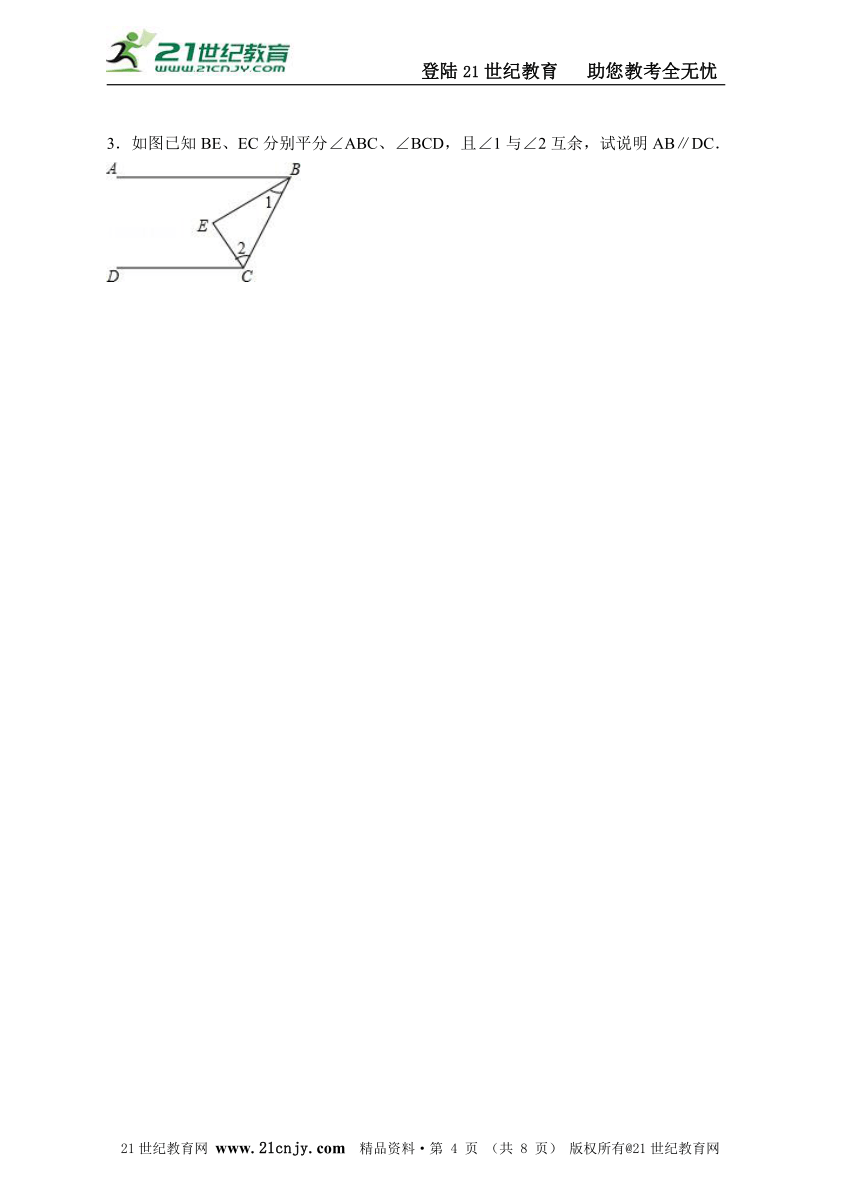
3．如图已知BE、EC分别平分∠ABC、∠BCD，且∠1与∠2互余，试说明AB∥DC．
参考答案
一．选择题(每小题5分，共35分)
1．D
【解析】∠3=∠5是同旁内角相等，但不一定互补，所以不能判定AB∥CD．
故选D．
2．D
【解析】A、两个角不是同位角、也不是内错角，故选项错误；
B、两个角不是同位角、也不是内错角，故选项错误；
C、不是EC和AB形成的同位角、也不是内错角，故选项错误；
D、正确．
故选D．
3．D
【解析】A、∵∠B=∠C=90°，
∴∠B+∠C=180°，
∴AB∥CD，A不可以；
B、∠B=∠D=90°，无法得出边平行的情况，B不可以；
C、AC=BD，无法得出边平行的情况，C不可以；
D、∵点A，D到BC的距离相等，且A、D在直线BC的同侧，
∴AD∥BC，D可以．
故选D．
4．C
【解析】∵∠1与∠2是内错角，
∴若∠1=∠2，则AD∥BC．
故选C．
5．B
【解答】A、∠3+∠4=180°不能判定任何直线平行，故本选项错误；
B、∵∠1=∠3，∠1+∠8=180°，∴∠3+∠8=180°，∴a∥b，故本选项正确；
C、∠5+∠7=180°不能判定任何直线平行，故本选项错误；
D、∠2+∠6=180°不能判定任何直线平行，故本选项错误．
故选B．
6．B
【解析】A、根据内错角相等，两直线平行可得BD∥AC，故此选项错误；
B、根据内错角相等，两直线平行可得AB∥CD，故此选项正确；
C、根据内错角相等，两直线平行可得BD∥AC，故此选项错误；
D、根据同旁内角互补，两直线平行可得BD∥AC，故此选项错误；
故选：B．
7．C
【解析】∠EDC=∠EFC不是两直线被第三条直线所截得到的，因而不能判定两直线平行；
∠AFE=∠ACD，∠1=∠2是EF和BC被AC所截得到的同位角和内错角，因而可以判定EF∥BC，但不能判定DE∥AC；21教育网
∠3=∠4这两个角是AC与DE被EC所截得到的内错角，可以判定DE∥AC．
故选C．
二．填空题(每小题5分，共20分)
1．②．
【解析】①∵∠3=∠4，∴AC∥BD，故本小题错误；
②∵∠1=∠2，∴AB∥CD，故本小题正确；
③当∠D=∠ACD时，不能判定任何直线平行，故本小题错误；
④∵∠D+∠ACD=180°，∴AC∥BD，故本小题错误．
故答案为：②．
2．∠FAD=∠FBC，或∠ADB=∠DBC，或∠DAB+∠ABC=180°．
【解析】添加∠FAD=∠FBC，或∠ADB=∠DBC，或∠DAB+∠ABC=180°．
∵∠FAD=∠FBC
∴AD∥BC（同位角相等两直线平行）；
∵∠ADB=∠DBC
∴AD∥BC（内错角相等两直线平行）；
∵∠DAB+∠ABC=180°
∴AD∥BC（同旁内角互补两直线平行）．
3．80°
【解析】如图，∵∠2=100°，
∴∠3=∠2=100°，
∴要使b与a平行，则∠1+∠3=180°，
∴∠1=180°﹣100°=80°．
故答案为：80°．
4．∠1=∠4（或∠6=∠7）．
【解析】∵∠1=∠4（己知），
∴BC∥AD（内错角相等，两直线平行）；
或∵∠6=∠7（己知），
∴BC∥AD（内错角相等，两直线平行）．
故答案为：∠1=∠4（或∠6=∠7）．
三．解答题(每小题15分，共45分)
1．（1）①135°；②40°；
（2）180°；
【解析】（1）①∵∠ECB=90°，∠DCE=45°，
∴∠DCB=90°﹣45°=45°，
∴∠ACB=∠ACD+∠DCB=90°+45°=135°，
故答案为：135°；
②∵∠ACB=140°，∠ACD=90°，
∴∠DCB=140°﹣90°=50°，
∴∠DCE=90°﹣50°=40°；
（2）∠ACB+∠DCE=180°，
∵∠ACB=∠ACD+∠DCB=90°+∠DCB，
∴∠ACB+∠DCE=90°+∠DCB+∠DCE=90°+90°=180°；
2．答案见解析．
【解析】∵DE平分∠BDC，
∴∠2=∠FDE；
∵∠1+∠2=90°，
∴∠BED=∠DEF=90°；
∴∠3+∠FDE=90°；
∴∠2+∠3=90°．
3．答案见解析．
【解析】∵∠1与∠2互余，
∴∠1+∠2=90°，
∵BE、EC分别平分∠ABC、∠BCD，
∴∠ABC=2∠1，∠BCD=2∠2，
∴∠ABC+∠BCD=2∠1+2∠2=2（∠1+∠2）=180°，
∴AB∥DC．