1.4平行线的性质（1） 同步练习

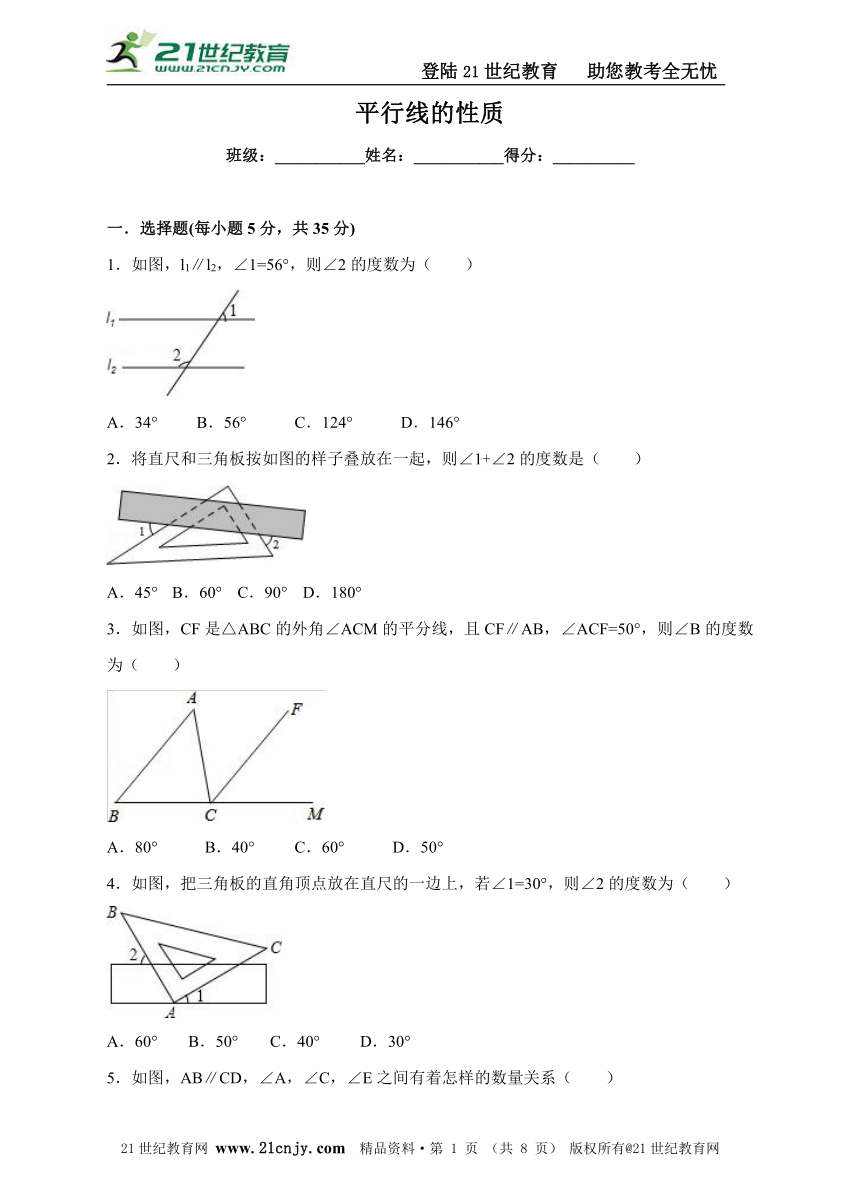
平行线的性质
班级：___________姓名：___________得分：__________
一．选择题(每小题5分，共35分)
1．如图，l1∥l2，∠1=56°，则∠2的度数为（　　）
A．34° B．56° C．124° D．146°
2．将直尺和三角板按如图的样子叠放在一起，则∠1+∠2的度数是（　　）
A．45° B．60° C．90° D．180°
3．如图，CF是△ABC的外角∠ACM的平分线，且CF∥AB，∠ACF=50°，则∠B的度数为（　　）21世纪教育网版权所有
A．80° B．40° C．60° D．50°
4．如图，把三角板的直角顶点放在直尺的一边上，若∠1=30°，则∠2的度数为（　　）
A．60° B．50° C．40° D．30°
5．如图，AB∥CD，∠A，∠C，∠E之间有着怎样的数量关系（　　）
A．∠E=∠A+∠C B．∠E=∠A﹣∠C
C．∠E=∠C﹣∠A D．∠E+∠A+∠C=180°
6．两平行直线被第三条直线所截，同位角的平分线（　　）
A．互相重合 B．互相平行 C．互相垂直 D．相交
7．如图，已知AB∥CD，∠C=65°，∠E=30°，则∠A的度数为（　　）
A．30° B．32.5° C．35° D．37.5°
二．填空题(每小题5分，共20分)
1．如图，点A、C、F、B在同一直线上，CD平分∠ECB，FG∥CD．若∠ECA=58°，则∠GFB的大小为 ．21教育网
2．如图，将三角板与直尺贴在一起，使三角板的直角顶点C（∠ACB=90°）在直尺的一边上，若∠2=65°，则∠1的度数等于　 　．21cnjy.com
3．一个角两边分别与∠ABC的两边平行，∠ABC=50°，则这个角等于　 　．
4．如图，直线a∥b，∠1=125°，则∠2=　 　°．
三．解答题(每小题15分，共45分)
1．如图，点D在射线AE上，AB∥CD，∠CDE=140°，求∠A的度数．
2．如图，已知射线AB与直线CD交于点O，OF平分∠BOC，OG⊥OF于O，AE∥OF，且∠A=30°．21·cn·jy·com
（1）求∠DOF的度数；
（2）试说明OD平分∠AOG．
3．如图，已知：a∥b，∠1=∠2，求证：c∥d．
参考答案
一．选择题(每小题5分，共35分)
1．C
【解析】∵l1∥l2，
∴∠1=∠3，
∵∠1=56°，
∴∠3=56°，
∵∠2+∠3=180°，
∴∠2=124°，
故选C．
2．C
【解析】如图，∵a∥b，
∴∠1=∠3，∠2=∠4．
又∵∠3=∠5，∠4=∠6，∠5+∠6=90°，
∴∠1+∠2=90°．
故选：C．
3．D
【解析】∵CF是∠ACM的平分线，
∴∠FCM=∠ACF=50°，
∵CF∥AB，
∴∠B=∠FCM=50°．
故选：D．
4．A
【解析】∵∠1=30°，
∴∠3=180°﹣90°﹣30°=60°，
∵直尺两边互相平行，
∴∠2=∠3=60°．
故选：A．
5．C
【解答】∵AB∥CD，
∴∠C=∠EMB，
∵∠EMB=∠A+∠E，
∴∠C=∠A+∠E，
故选C．
6．B
【解析】∵两平行直线被第三条直线所截，同位角相等，
∴它们角的平分线形成的同位角相等，
∴同位角相等的平分线平行．
故选B．
7．C
【解析】设AB、CE交于点O．
∵AB∥CD，∠C=65°，
∴∠EOB=∠C=65°，
∵∠E=30°，
∴∠A=∠EOB﹣∠E=35°，
故选：C．
二．填空题(每小题5分，共20分)
1．61°．
【解析】∵∠ECA=58°，
∴∠ECD=180°﹣∠ECA=122°，
∵CD平分∠ECF，
∴∠DCF=∠ECF=×122°=61°，
∵CD∥GF，
∴∠GFB=∠DCF=61°．
故答案为61°．
2．25°．
【解析】∵直尺的两边互相平行，∠2=65°，
∴∠3=∠2=65°．
∵∠ACB=90°，
∴∠1=90°﹣∠2=90°﹣65°=25°．
故答案为：．
3．130°或50°．
【解析】设这个角的度数是x°，
∵一个角两边分别与∠ABC的两边平行，∠ABC=50°，
∴x+50=180或x=50，
即这个角是130°或50°，
故答案为：130°或50°．
4．55．
【解析】∵∠1=125°，
∴∠3=180°﹣∠1=180°﹣125°=55°，
∵a∥b，
∴∠2=∠3=55°．
故答案为：55．
三．解答题(每小题15分，共45分)
1．40°
【解析】延长CD，
∵∠CDE=140°，
∴∠EDF=40°．
∵AB∥CD，
∴∠A=∠EDF=40°．
2．（1）150°；
（2）答案见解析
【解析】（1）∵AE∥OF，
∴∠FOB=∠A=30°，
∵OF平分∠BOC，
∴∠COF=∠FOB=30°，
∴∠DOF=180°﹣∠COF=150°；
（2）∵OF⊥OG，
∴∠FOG=90°，
∴∠DOG=∠DOF﹣∠FOG=150°﹣90°=60°，
∵∠AOD=∠COB=∠COF+∠FOB=60°，
∴∠AOD=∠DOG，
∴OD平分∠AOG．
3．答案见解析．
【解析】如图所示，
∵a∥b，
∴∠1=∠3，
∵∠1=∠2，
∴∠2=∠3，
∴c∥d．