《用球面多边形的内角和公式证明欧拉公式》课件
文档属性
| 名称 | 《用球面多边形的内角和公式证明欧拉公式》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 135.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-28 17:41:07 | ||
图片预览


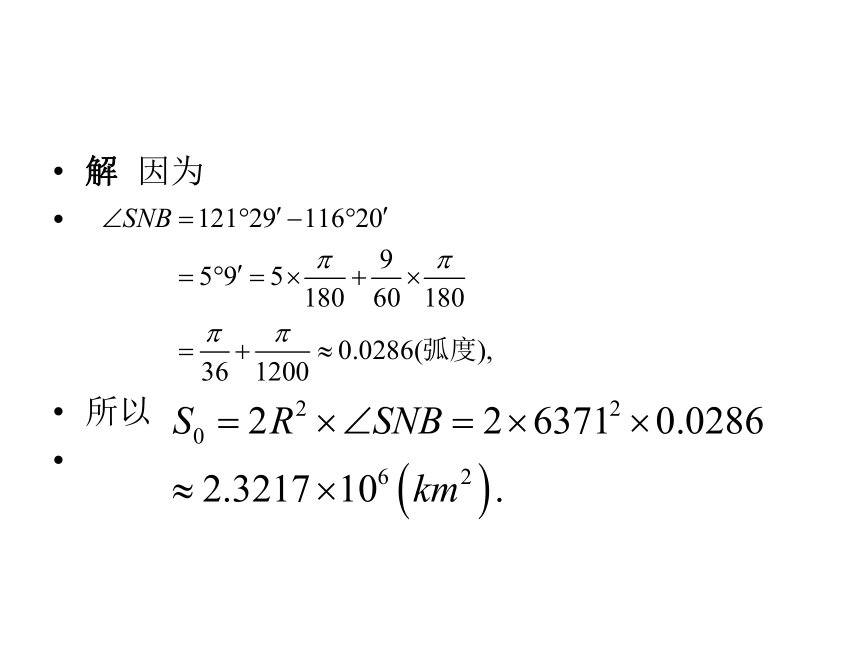

文档简介
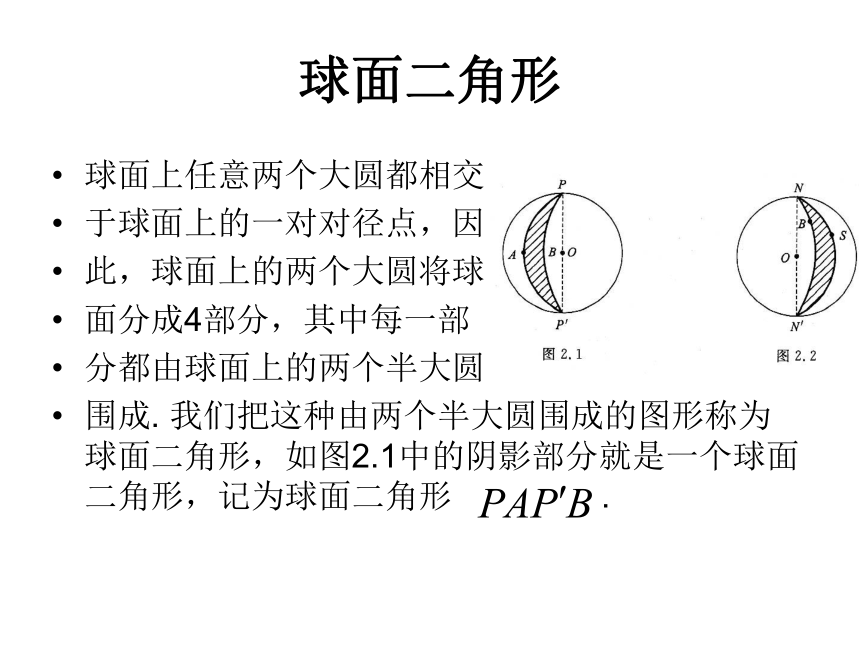
课件13张PPT。用球面多边形的内角和公式证明欧拉公式球面二角形 球面上任意两个大圆都相交
于球面上的一对对径点,因
此,球面上的两个大圆将球
面分成4部分,其中每一部
分都由球面上的两个半大圆
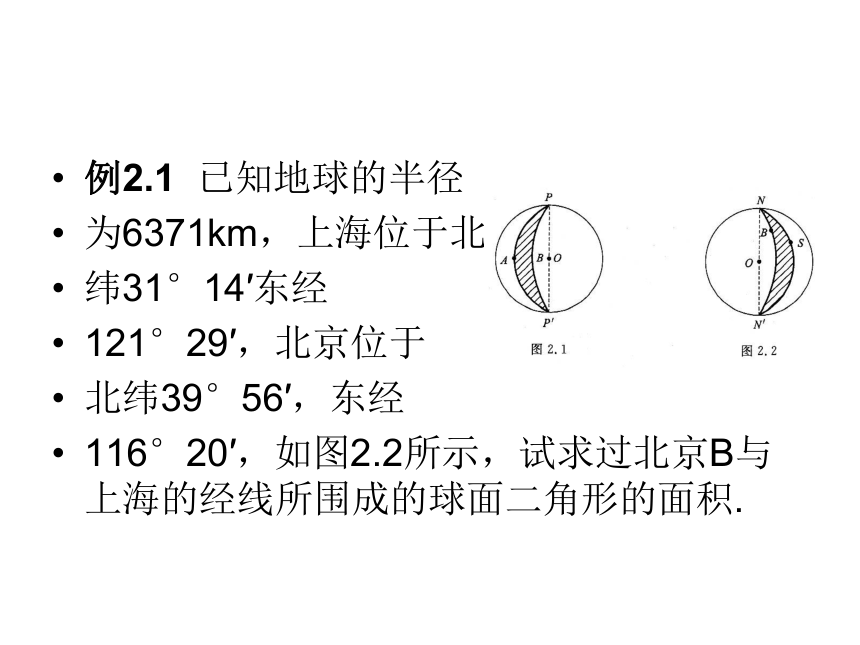
围成. 我们把这种由两个半大圆围成的图形称为球面二角形,如图2.1中的阴影部分就是一个球面二角形,记为球面二角形 . 球面二角形 的元素对于球面二角形,我们把对径点 P与 称为这个二角形的顶点,半大圆弧 与 称为这个二角形的边,球面角 与球面角 称为这个二角形的内角,在不产生混淆的情况下,简记为 ,它们既表示二角形的两个内角,也表示这两角内角的大小.例2.1 已知地球的半径
为6371km,上海位于北
纬31°14′东经
121°29′,北京位于
北纬39°56′,东经
116°20′,如图2.2所示,试求过北京B与上海的经线所围成的球面二角形的面积.解 因为
所以
球面三角形 设A,B,C是球面上不在同一条球面直线上的三点,我们把其中任两点用球面线段连接. 所得的图形称为球面三角形球面三角形,记为球面 . 点A,B,C称为这个球面三角形的顶点,球面线段
称为这个球面三角形的边,三边的长称为这个球面三角形的边长,也用记号 .定理2.1 定理2.1 球面三角形的面积等于它的三内角和减去的差再乘以球面半径的平方,即
. (2.1)
其中,R为球面的半径.证 如图2.3所示,设点A,B,C的对径点分别为
将球面角CAB的边AC与AB延长至 ,得球面二角形 . 我们用 表示球面 的面积,用A表示球面角A的弧度数,其他球面三角形的面积与球面角的弧度数采用类似的记法,则有
. 推论 推论1 对于单位球面上的球面 ,有
.推论2 球面三角形三内角和大于 .例2.2 设球面的半径为 ,点P是球线
段 的极,求球面 的面积.谢谢
于球面上的一对对径点,因
此,球面上的两个大圆将球
面分成4部分,其中每一部
分都由球面上的两个半大圆
围成. 我们把这种由两个半大圆围成的图形称为球面二角形,如图2.1中的阴影部分就是一个球面二角形,记为球面二角形 . 球面二角形 的元素对于球面二角形,我们把对径点 P与 称为这个二角形的顶点,半大圆弧 与 称为这个二角形的边,球面角 与球面角 称为这个二角形的内角,在不产生混淆的情况下,简记为 ,它们既表示二角形的两个内角,也表示这两角内角的大小.例2.1 已知地球的半径
为6371km,上海位于北
纬31°14′东经
121°29′,北京位于
北纬39°56′,东经
116°20′,如图2.2所示,试求过北京B与上海的经线所围成的球面二角形的面积.解 因为
所以
球面三角形 设A,B,C是球面上不在同一条球面直线上的三点,我们把其中任两点用球面线段连接. 所得的图形称为球面三角形球面三角形,记为球面 . 点A,B,C称为这个球面三角形的顶点,球面线段
称为这个球面三角形的边,三边的长称为这个球面三角形的边长,也用记号 .定理2.1 定理2.1 球面三角形的面积等于它的三内角和减去的差再乘以球面半径的平方,即
. (2.1)
其中,R为球面的半径.证 如图2.3所示,设点A,B,C的对径点分别为
将球面角CAB的边AC与AB延长至 ,得球面二角形 . 我们用 表示球面 的面积,用A表示球面角A的弧度数,其他球面三角形的面积与球面角的弧度数采用类似的记法,则有
. 推论 推论1 对于单位球面上的球面 ,有
.推论2 球面三角形三内角和大于 .例2.2 设球面的半径为 ,点P是球线
段 的极,求球面 的面积.谢谢
同课章节目录
- 第一讲 从欧氏几何看球面
- 一 平面与球面的位置关系
- 二 直线与球面的位置关系和球幂定理
- 三 球面的对称性
- 第二讲 球面上的距离和角
- 一 球面上的距离
- 二 球面上的角
- 第三讲 球面上的基本图形
- 一 极与赤道
- 二 球面二角形
- 三 球面三角形
- 第四讲 球面三角形
- 一 球面三角形三边之间的关系
- 二 球面“等腰”三角形
- 三 球面三角形的周长
- 四 球面三角形的内角和
- 第五讲 球面三角形的全等
- 1.“边边边”(s.s.s)判定定理
- 2.“边角边”(s.a.s.)判定定理
- 3.“角边角”(a.s.a.)判定定理
- 4.“角角角”(a.a.a.)判定定理
- 第六讲 球面多边形与欧拉公式
- 一 球面多边形及其内角和公式
- 二 简单多面体的欧拉公式
- 三 用球面多边形的内角和公式证明欧拉公式
- 第七讲 球面三角形的边角关系
- 一 球面上的正弦定理和余弦定理
- 二 用向量方法证明球面上的余弦定理
- 三 从球面上的正弦定理看球面与平面
- 四 球面上余弦定理的应用──求地球上两城市间的距离
- 第八讲 欧氏几何与非欧几何
- 一 平面几何与球面几何的比较
- 二 欧氏平行公理与非欧几何模型──庞加莱模型
- 三 欧氏几何与非欧几何的意义
