《角边角判定定理》课件

课件6张PPT。角边角判定定理证明AAS：
AAS,即角角边，已知两个三角形对应的两个角和其中一个角的对边，问两个三角形是否全等？或已知两个角和其中一个角的对边，问此三角形是否唯一。首先已知两个角，也可以算出第三个角的度数，再根据ASA证明三角形全等。证明方法如下：∵已知∠a与∠b，∠a+∠b+∠c=180°∴得知∠c
∵已知∠a，线段C，∠c，
所以三角形是唯一（ASA）。
在AAS中，
已知AA两个角，根据三角形内角和等于180°，可以证明剩下的一对角相等
然后因ASA可证明三角形全等，
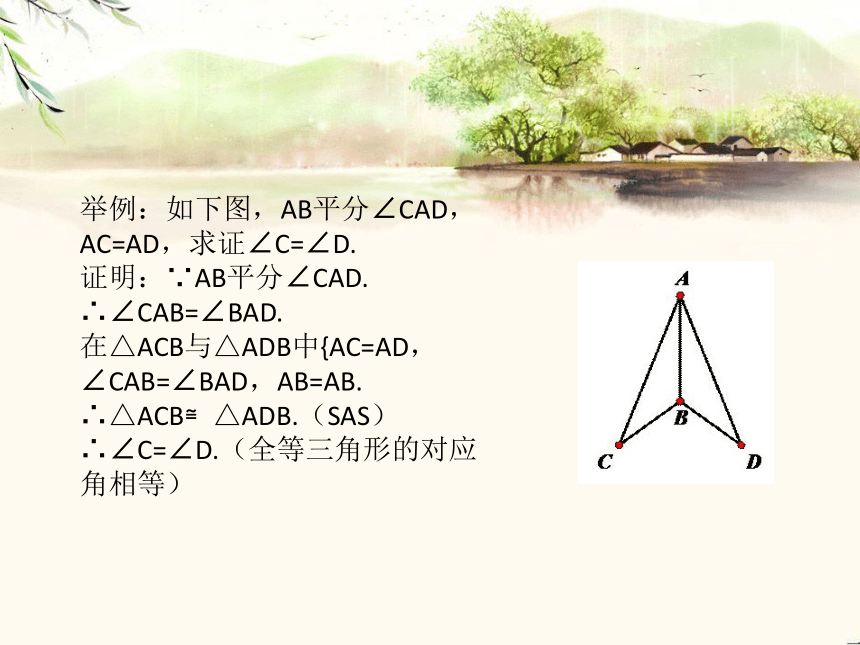
所以AAS也可以证明三角形全等。普通三角形举例：如下图，AB平分∠CAD，AC=AD，求证∠C=∠D.
证明：∵AB平分∠CAD.
∴∠CAB=∠BAD.
在△ACB与△ADB中{AC=AD，∠CAB=∠BAD，AB=AB.
∴△ACB≌△ADB.（SAS）
∴∠C=∠D.（全等三角形的对应角相等）球面三角形的解法已知两角夹边解该三角形
例题：
在球面三角形中，
已知 a＝50°44′.0，
B＝ 69°12′.0，
C＝115 °55 ′.4，
求 c。
应用四联公式：边的外余切内正弦等于角的外余切内正弦加上双内余弦之积
ctgcsina=ctgCsinB+cosacosb
注意应用的时候要注意使用正确的方法谢谢