1.3 平行线的判定 一课一练

21世纪教育网 –中小学教育资源及组卷应用平台
1.3平行线的判定 一课一练
姓名：__________班级：__________学号：__________
本节应掌握和应用的知识点：
1.平行线的判定方法
2.学会用平行线的判定方法进行简单的几何推理
基础知识和能力拓展精练
一．选择题（共10小题）
1．如图，直线a，b被直线c所截，下列条件不能判定直线a与b平行的是（　　）
A．∠1=∠3 B．∠2+∠4=180° C．∠1=∠4 D．∠3=∠4
2．如图为平面上五条直线L1，L2，L3，L4，L5相交的情形，根据图中标示的角度，判断下列叙述何者正确（　　）
A．L1和L3平行，L2和L3平行 B．L1和L3平行，L2和L3不平行
C．L1和L3不平行，L2和L3平行 D．L1和L3不平行，L2和L3不平行
3．如图，下列说法错误的是（　　）
A．若a∥b，b∥c，则a∥c B．若∠1=∠2，则a∥c
C．若∠3=∠2，则b∥c D．若∠3+∠5=180°，则a∥c
4．如图，直线l1、l2被直线l3、l4所截，下列条件中，不能判断直线l1∥l2的是（　　）
A．∠1=∠3 B．∠5=∠4 C．∠5+∠3=180° D．∠4+∠2=180°
5．如图，下列条件中能判定直线l1∥l2的是（　　）
A．∠1=∠2 B．∠1=∠5 C．∠1+∠3=180° D．∠3=∠5
6．如图，在下列条件中，能判断AD∥BC的是（　　）
A．∠DAC=∠BCA B．∠DCB+∠ABC=180°
C．∠ABD=∠BDC D．∠BAC=∠ACD
7．如图，点E在AC的延长线上，下列条件中能判断AB∥CD的是（　　）
A．∠3=∠4 B．∠D=∠DCE C．∠1=∠2 D．∠D+∠ACD=180°
8．如图，直线AB，CD被直线EF所截，∠1=55°，下列条件中能判定AB∥CD的是（　　）
A．∠2=35° B．∠2=45° C．∠2=55° D．∠2=125°
9．如图，直线a，b被直线c所截，下列条件能判断a∥b的是（　　）
A．∠1=∠2 B．∠1=∠4 C．∠3+∠4=180° D．∠2=30°，∠4=35°
10．下列选项中，哪个不可以得到l1∥l2？（　　）
A．∠1=∠2 B．∠2=∠3 C．∠3=∠5 D．∠3+∠4=180°
　
二．填空题（共6小题）
11．如图，直线a、b被直线c所截，若满足　 　，则a、b平行．
12．如图，B、A、E三点在同一直线上，请你添加一个条件，使AD∥BC．你所添加的条件是　 　（不允许添加任何辅助线）．
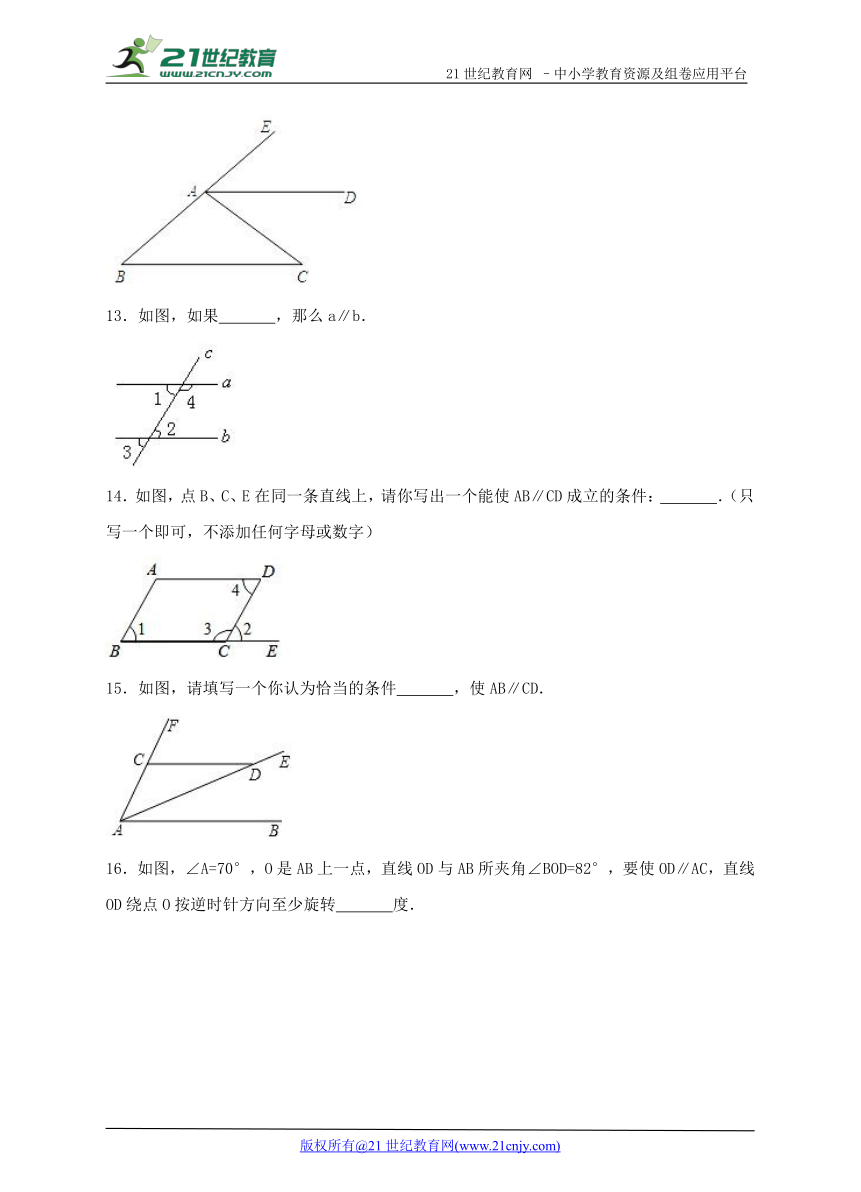
13．如图，如果　 　，那么a∥b．
14．如图，点B、C、E在同一条直线上，请你写出一个能使AB∥CD成立的条件：　 　．（只写一个即可，不添加任何字母或数字）
15．如图，请填写一个你认为恰当的条件　 　，使AB∥CD．
16．如图，∠A=70°，O是AB上一点，直线OD与AB所夹角∠BOD=82°，要使OD∥AC，直线OD绕点O按逆时针方向至少旋转　 　度．
　
三．解答题（共8小题）
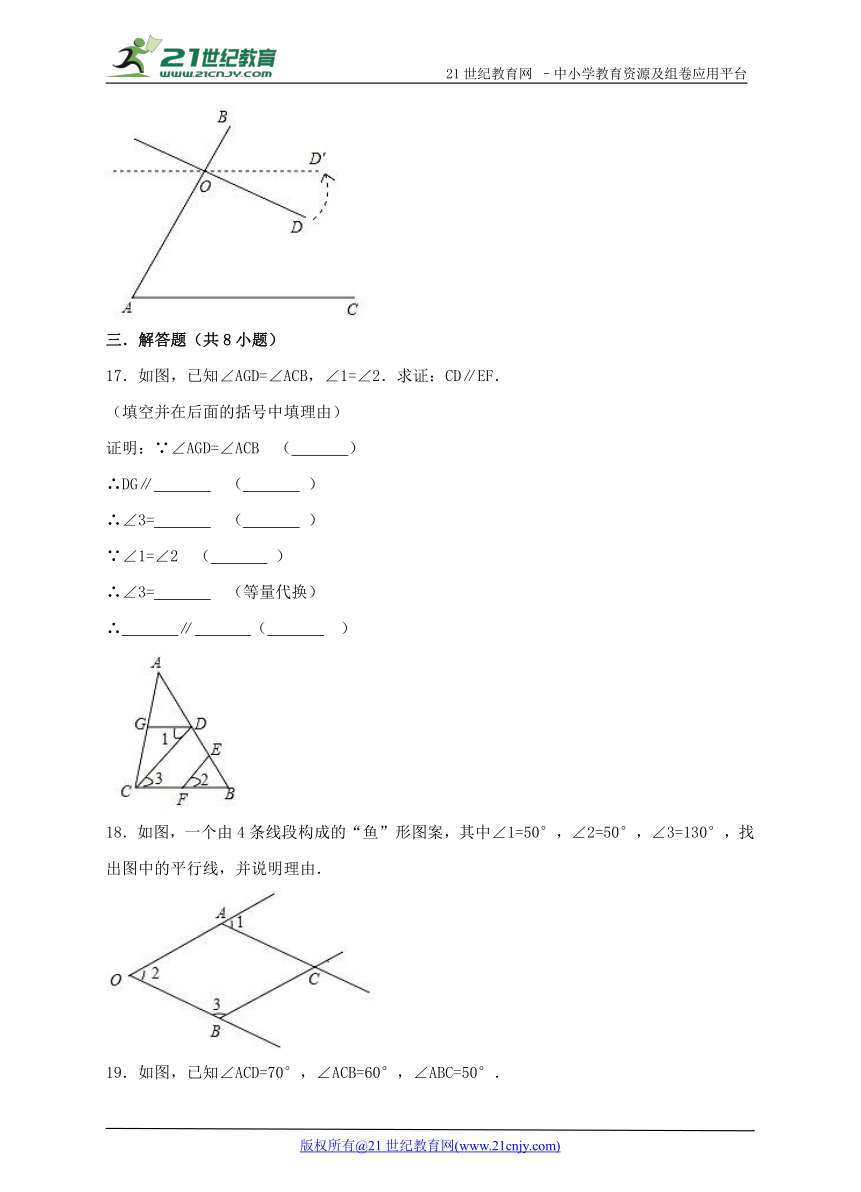
17．如图，已知∠AGD=∠ACB，∠1=∠2．求证：CD∥EF．
（填空并在后面的括号中填理由）
证明：∵∠AGD=∠ACB　（　 　）
∴DG∥　 　　（　 　 ）
∴∠3=　 　　（　 　 ）
∵∠1=∠2　（　 　 ）
∴∠3=　 　　（等量代换）
∴　 　∥　 　（　 　 ）
18．如图，一个由4条线段构成的“鱼”形图案，其中∠1=50°，∠2=50°，∠3=130°，找出图中的平行线，并说明理由．
19．如图，已知∠ACD=70°，∠ACB=60°，∠ABC=50°．
求证：AB∥CD．
20．如图，已知AB=AC=AD，且∠C=2∠D，求证AD∥BC．
21．如图，∠BAF=46°，∠ACE=136°，CE⊥CD．问CD∥AB吗？为什么？
22．如图，已知：△ABC，E为AB上一点，D，F分别为AC上的点，∠AED=60°，∠2=30°，EF平分∠AED，求证：EF∥BD．
23．已知：如图，∠A=∠ADE，∠C=∠E．
（1）若∠EDC=3∠C，求∠C的度数．
（2）求证：BE∥CD．
24．如图，点D，E在AB，AC上，连接DE，DF平分∠BDE交BC于点F，∠BDF+∠DFC=180°，∠AED=∠BFD．
（1）DE与BC平行吗？并写出理由；
（2）写出图中与∠CED相等的角及理由．
　
参考答案与试题解析
　
一．选择题（共10小题）
1．如图，直线a，b被直线c所截，下列条件不能判定直线a与b平行的是（　　）
A．∠1=∠3 B．∠2+∠4=180° C．∠1=∠4 D．∠3=∠4
【分析】根据同位角相等，两直线平行；同旁内角互补，两直线平行进行判断即可．
解：由∠1=∠3，可得直线a与b平行，故A能判定；
由∠2+∠4=180°，∠2=∠5，∠4=∠3，可得∠3+∠5=180°，故直线a与b平行，故B能判定；
由∠1=∠4，∠4=∠3，可得∠1=∠3，故直线a与b平行，故C能判定；
由∠3=∠4，不能判定直线a与b平行，
故选：D．
　
2．如图为平面上五条直线L1，L2，L3，L4，L5相交的情形，根据图中标示的角度，判断下列叙述何者正确（　　）
A．L1和L3平行，L2和L3平行
B．L1和L3平行，L2和L3不平行
C．L1和L3不平行，L2和L3平行
D．L1和L3不平行，L2和L3不平行
【分析】根据同旁内角不互补，可得两直线不平行；根据内错角相等，可得两直线平行．
解：∵92°+92°≠180°，
∴L1和L3不平行，
∵88°=88°，
∴L2和L3平行，
故选：C．
　
3．如图，下列说法错误的是（　　）
A．若a∥b，b∥c，则a∥c B．若∠1=∠2，则a∥c
C．若∠3=∠2，则b∥c D．若∠3+∠5=180°，则a∥c
【分析】根据平行线的判定进行判断即可．
解：A、若a∥b，b∥c，则a∥c，利用了平行公理，正确；
B、若∠1=∠2，则a∥c，利用了内错角相等，两直线平行，正确；
C、∠3=∠2，不能判断b∥c，错误；
D、若∠3+∠5=180°，则a∥c，利用同旁内角互补，两直线平行，正确；
故选C．
　
4．如图，直线l1、l2被直线l3、l4所截，下列条件中，不能判断直线l1∥l2的是（　　）
A．∠1=∠3 B．∠5=∠4 C．∠5+∠3=180° D．∠4+∠2=180°
【分析】依据平行线的判定定理即可判断．
解：A、已知∠1=∠3，根据内错角相等，两直线平行可以判断，故命题正确；
B、不能判断；
C、同旁内角互补，两直线平行，可以判断，故命题正确；
D、同旁内角互补，两直线平行，可以判断，故命题正确．
故选B．
　
5．如图，下列条件中能判定直线l1∥l2的是（　　）
A．∠1=∠2 B．∠1=∠5 C．∠1+∠3=180° D．∠3=∠5
【分析】平行线的判定定理有：①同位角相等，两直线平行；②内错角相等，两直线平行；③同旁内角互补，两直线平行．
根据以上内容判断即可．
解：A、根据∠1=∠2不能推出l1∥l2，故A选项错误；
B、∵∠5=∠3，∠1=∠5，
∴∠1=∠3，
即根据∠1=∠5不能推出l1∥l2，故B选项错误；
C、∵∠1+∠3=180°，
∴l1∥l2，故C选项正确；
D、根据∠3=∠5不能推出l1∥l2，故D选项错误；
故选：C．
　
6．如图，在下列条件中，能判断AD∥BC的是（　　）
A．∠DAC=∠BCA B．∠DCB+∠ABC=180°
C．∠ABD=∠BDC D．∠BAC=∠ACD
【分析】根据各选项中各角的关系及利用平行线的判定定理，分别分析判断AD、BC是否平行即可．
解：A、∵∠DAC=∠BCA，∴AD∥BC（内错角相等，两直线平行），故A正确；
B、根据“∠DCB+∠ABC=180°”只能判定“DC∥AB”，而非AD∥BC，故B错误；
C、根据“∠ABD=∠BDC”只能判定“DC∥AB”，而非AD∥BC，故C错误；
D、根据“∠BAC=∠ACD”只能判定“DC∥AB”，而非AD∥BC，故D错误；
故选：A．
　
7．如图，点E在AC的延长线上，下列条件中能判断AB∥CD的是（　　）
A．∠3=∠4 B．∠D=∠DCE C．∠1=∠2 D．∠D+∠ACD=180°
【分析】由平行线的判定定理可证得，选项A，B，D能证得AC∥BD，只有选项C能证得AB∥CD．注意掌握排除法在选择题中的应用．
解：A、∵∠3=∠4，
∴AC∥BD．
本选项不能判断AB∥CD，故A错误；
B、∵∠D=∠DCE，
∴AC∥BD．
本选项不能判断AB∥CD，故B错误；
C、∵∠1=∠2，
∴AB∥CD．
本选项能判断AB∥CD，故C正确；
D、∵∠D+∠ACD=180°，
∴AC∥BD．
故本选项不能判断AB∥CD，故D错误．
故选：C．
　
8．如图，直线AB，CD被直线EF所截，∠1=55°，下列条件中能判定AB∥CD的是（　　）
A．∠2=35° B．∠2=45° C．∠2=55° D．∠2=125°
【分析】根据平行线的判定定理对各选项进行逐一判断即可．
解：A、由∠3=∠2=35°，∠1=55°推知∠1≠∠3，故不能判定AB∥CD，故本选项错误；
B、由∠3=∠2=45°，∠1=55°推知∠1≠∠3，故不能判定AB∥CD，故本选项错误；
C、由∠3=∠2=55°，∠1=55°推知∠1=∠3，故能判定AB∥CD，故本选项正确；
D、由∠3=∠2=125°，∠1=55°推知∠1≠∠3，故不能判定AB∥CD，故本选项错误；
故选：C．
　
9．如图，直线a，b被直线c所截，下列条件能判断a∥b的是（　　）
A．∠1=∠2 B．∠1=∠4
C．∠3+∠4=180° D．∠2=30°，∠4=35°
【分析】根据同位角相等，两直线平行即可判断．
解：∵∠1=∠4，
∴a∥b（同位角相等两直线平行）．
故选B．
　
10．下列选项中，哪个不可以得到l1∥l2？（　　）
A．∠1=∠2 B．∠2=∠3 C．∠3=∠5 D．∠3+∠4=180°
【分析】分别根据平行线的判定定理对各选项进行逐一判断即可．
解：A、∵∠1=∠2，∴l1∥l2，故本选项错误；
B、∵∠2=∠3，∴l1∥l2，故本选项错误；
C、∠3=∠5不能判定l1∥l2，故本选项正确；
D、∵∠3+∠4=180°，∴l1∥l2，故本选项错误．
故选C．
　
二．填空题（共6小题）
11．如图，直线a、b被直线c所截，若满足　∠1=∠2或∠2=∠3或∠3+∠4=180°　，则a、b平行．
【分析】根据同位角或内错角相等以及同旁内角互补，两直线平行可得a∥b．
解：∵∠1=∠2，
∴a∥b（同位角相等两直线平行），
同理可得：∠2=∠3或∠3+∠4=180°时，a∥b，
故答案为：∠1=∠2或∠2=∠3或∠3+∠4=180°．
　
12．如图，B、A、E三点在同一直线上，请你添加一个条件，使AD∥BC．你所添加的条件是　∠EAD=∠B或∠DAC=∠C或∠DAB+∠B=180°　（不允许添加任何辅助线）．
【分析】使AD∥BC判别两条直线平行的方法有：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．因而可以添加的条件是∠EAD=∠B或∠DAC=∠C或∠DAB+∠B=180°．
可以添加的条件是∠EAD=∠B，依据同位角相等，两直线平行；
或∠DAC=∠C，依据内错角相等，两直线平行；
或∠DAB+∠B=180°，依据同旁内角互补，两直线平行．
故答案为：∠EAD=∠B或∠DAC=∠C或∠DAB+∠B=180°．
　
13．如图，如果　∠1=∠2　，那么a∥b．
【分析】判别两条直线平行的方法有：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．因而∠1=∠2或∠3=∠1，或∠2+∠4=180°都可以得到a∥b．
解：如果∠1=∠2，那么a∥b．
　
14．如图，点B、C、E在同一条直线上，请你写出一个能使AB∥CD成立的条件：　∠1=∠2　．（只写一个即可，不添加任何字母或数字）
【分析】欲证AB∥CD，在图中发现AB、CD被一直线所截，故可按同旁内角互补两直线平行补充条件或同位角相等两直线平行补充条件．
解：要使AB∥CD，
则只要∠1=∠2（同位角相等两直线平行），
或只要∠1+∠3=180°（同旁内角互补两直线平行）．
故答案为∠1=∠2（答案不唯一）．
　
15．如图，请填写一个你认为恰当的条件　∠CDA=∠DAB或∠FCD=∠FAB或∠BAC+∠ACD=180°　，使AB∥CD．
【分析】欲证AB∥CD，在图中发现AB、CD被直线AC或AD所截，然后根据平行线的判定方法寻找同位角或内错角或同旁内角就可．
解：根据同位角相等，两条直线平行，可以添加∠FCD=∠FAB；
根据内错角相等，两条直线平行，可以添加∠CDA=∠DAB；
根据同旁内角互补，两条直线平行，可以添加∠BAC+∠ACD=180°．
　
16．如图，∠A=70°，O是AB上一点，直线OD与AB所夹角∠BOD=82°，要使OD∥AC，直线OD绕点O按逆时针方向至少旋转　12　度．
【分析】根据OD∥AC，两直线平行，同位角相等，求得∠BOD'=∠A，即可得到∠DOD'的度数，即旋转角．
解：∵OD∥AC，
∴∠BOD'=∠A=70°，
∴∠DOD'=82°﹣70°=12°．
故答案是：12．
　
三．解答题（共8小题）
17．如图，已知∠AGD=∠ACB，∠1=∠2．求证：CD∥EF．
（填空并在后面的括号中填理由）
证明：∵∠AGD=∠ACB　（　已知　）
∴DG∥　CB　　（　同位角相等，两直线平行　 ）
∴∠3=　∠1　　（　两直线平行，内错角相等　 ）
∵∠1=∠2　（　已知　 ）
∴∠3=　∠2　　（等量代换）
∴　CD　∥　EF　（　同位角相等，两直线平行　 ）
【分析】根据平行线的判定首先得出DG∥CB，再利用平行线的性质得出∠3=∠2，进而得出CD∥EF．
证明：∵∠AGD=∠ACB　（已知），
∴DG∥CB（同位角相等，两直线平行），
∴∠3=∠1　（两直线平行，内错角相等 ），
∵∠1=∠2　（已知），
∴∠3=∠2（等量代换），
∴CD∥EF（同位角相等，两直线平行）．
　
18．如图，一个由4条线段构成的“鱼”形图案，其中∠1=50°，∠2=50°，∠3=130°，找出图中的平行线，并说明理由．
【分析】根据同位角相等，两直线平行证明OB∥AC，根据同旁内角互补，两直线平行证明OA∥BC．
解：OA∥BC，OB∥AC．
∵∠1=50°，∠2=50°，
∴∠1=∠2，
∴OB∥AC，
∵∠2=50°，∠3=130°，
∴∠2+∠3=180°，
∴OA∥BC．
　
19．如图，已知∠ACD=70°，∠ACB=60°，∠ABC=50°．
求证：AB∥CD．
【分析】求出∠ABC+∠BCD=180°，根据平行线的判定推出即可．
证明：∵∠ACD=70°，∠ACB=60°，
∴∠BCD=∠ACB+∠ACD=130°，
∵∠ABC=50°，
∴∠ABC+∠BCD=180°，
∴AB∥CD．
　
20．如图，已知AB=AC=AD，且∠C=2∠D，求证AD∥BC．
【分析】欲证明AD∥BC，只需推知∠CBD=∠D即可．
证明：∵AB=AC=AD，
∴∠C=∠ABC，∠D=∠ABD，
∵∠C=2∠D，
∴∠ABC=2∠ABD，
∴∠ABD=∠CBD=∠D，
∴AD∥BC．
　
21．如图，∠BAF=46°，∠ACE=136°，CE⊥CD．问CD∥AB吗？为什么？
【分析】根据已知条件求出关于直线CD，AB的内错角的度数，看它们是否相等，以此来判定两直线是否平行．
解：CD∥AB．
证明：∵CE⊥CD，
∴∠DCE=90°，
∵∠ACE=136°，
∴∠ACD=360°﹣136°﹣90°=134°，
∵∠BAF=46°，
∴∠BAC=180°﹣∠BAF=180°﹣46°=134°，
∴∠ACD=∠BAC，
∴CD∥AB．
　
22．如图，已知：△ABC，E为AB上一点，D，F分别为AC上的点，∠AED=60°，∠2=30°，EF平分∠AED，求证：EF∥BD．
【分析】先由角平分线定义得出∠FED=30°，那么∠FED=∠2=30°，根据内错角相等，两直线平行即可证明EF∥BD．
证明：∵∠AED=60°，EF平分∠AED，
∴∠FED=30°，
∵∠2=30°，
∴∠FED=∠2，
∴EF∥BD．
　
23．已知：如图，∠A=∠ADE，∠C=∠E．
（1）若∠EDC=3∠C，求∠C的度数．
（2）求证：BE∥CD．
【分析】（1）根据两直线平行，同旁内角互补，即可得出∠C的度数；
（2）根据AC∥DE，∠C=∠E，即可得出∠C=∠ABE，进而判定BE∥CD．
解：（1）∵∠A=∠ADE，
∴AC∥DE，
∴∠EDC+∠C=180°，
又∵∠EDC=3∠C，
∴4∠C=180°，
即∠C=45°；
（2）∵AC∥DE，
∴∠E=∠ABE，
又∵∠C=∠E，
∴∠C=∠ABE，
∴BE∥CD．
　
24．如图，点D，E在AB，AC上，连接DE，DF平分∠BDE交BC于点F，∠BDF+∠DFC=180°，∠AED=∠BFD．
（1）DE与BC平行吗？并写出理由；
（2）写出图中与∠CED相等的角及理由．
【分析】（1）由DF平分∠BDE易得∠EDF=∠BDF，又∠BDF+∠DFC=180°可得∠EDF+∠DFC=180°，由平行线的判定定理可得结论；
（2）∠AED=∠BFD可得∠CED=∠CFD．
解：（1）平行．
∵DF平分∠BDE，
∴∠EDF=∠BDF，
∵∠BDF+∠DFC=180°，
∴∠EDF+∠DFC=180°
∴DE∥BC；
（2）∠CED=∠CFD．
∵∠AED+∠CED=180°，∠BFD+CFD=180°，
又∵∠AED=∠BFD，
∴∠CED=∠CFD．
　
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)