1.5 图形的平移一课一练

21世纪教育网 –中小学教育资源及组卷应用平台
1.5图形的平移 一课一练
姓名：__________班级：__________学号：__________
本节应掌握和应用的知识点：
1.平移的定义
2.平移的性质
3.平移性质的应用
基础知识和能力拓展精练
一．选择题（共10小题）
1．下列生活中的各个现象，属于平移变换现象的是（　　）
A．拉开抽屉 B．用放大镜看文字 C．时钟上分针的运动 D．你和平面镜中的像
2．下列哪个图形是由如图平移得到的（　　）
A． B． C． D．
3．下列图形中，不能通过其中一个四边形平移得到的是（　　）
A． B． C． D．
4．下列现象属于平移的有（　　）个．
①气筒活塞的往复运动，②荡秋千，③钟摆的摆动，④转动的门．
A．2 B．3 C．1 D．4
5．如图，△DEF是由△ABC通过平移得到，且点B，E，C，F在同一条直线上．若BF=14，EC=6．则BE的长度是（　　）
A．2 B．4 C．5 D．3
6．下列说法不正确的是（　　）
A．把一个图形平移到一个确定位置，大小形状都不变
B．在平移图形的过程中，图形上的各点坐标发生同样的变化
C．在平移过程中图形上的个别点的坐标不变
D．平移后的两个图形的对应角相等，对应边相等，对应边平行或共线
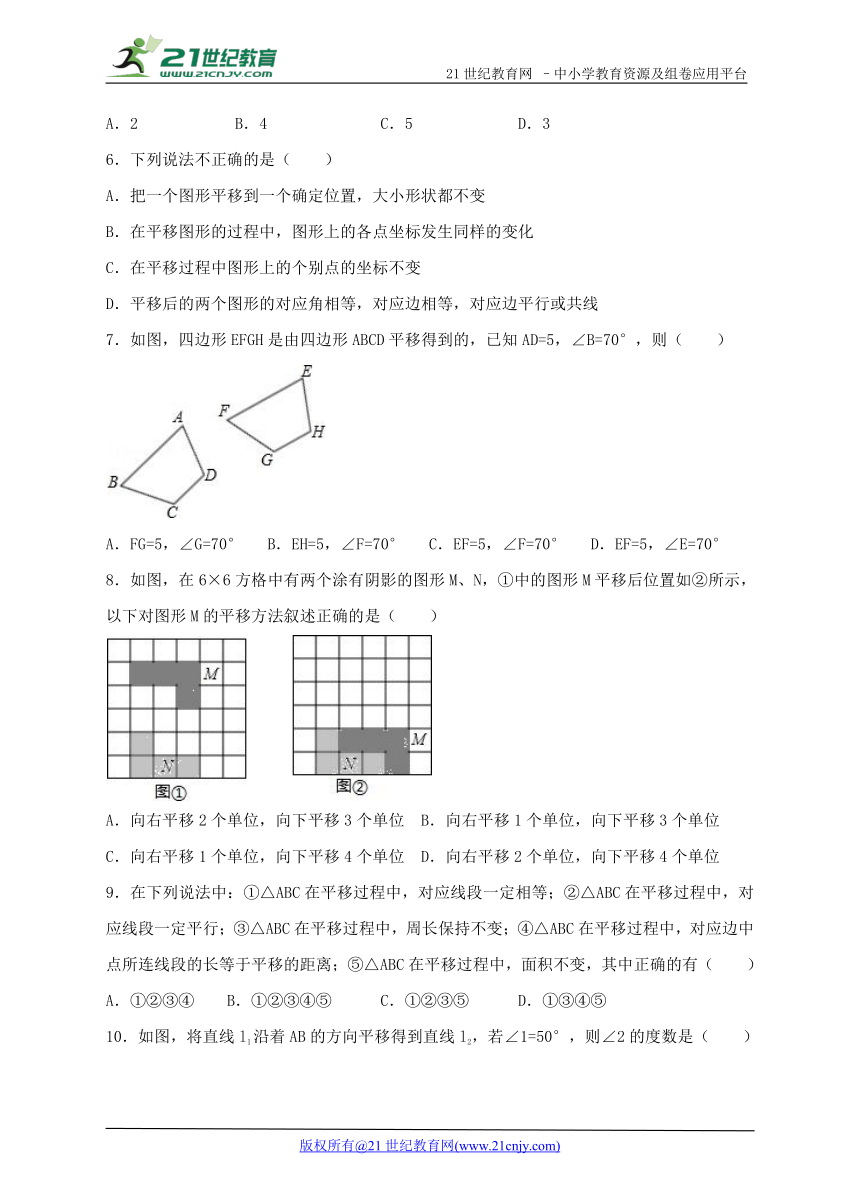
7．如图，四边形EFGH是由四边形ABCD平移得到的，已知AD=5，∠B=70°，则（　　）
A．FG=5，∠G=70° B．EH=5，∠F=70° C．EF=5，∠F=70° D．EF=5，∠E=70°
8．如图，在6×6方格中有两个涂有阴影的图形M、N，①中的图形M平移后位置如②所示，以下对图形M的平移方法叙述正确的是（　　）
A．向右平移2个单位，向下平移3个单位 B．向右平移1个单位，向下平移3个单位
C．向右平移1个单位，向下平移4个单位 D．向右平移2个单位，向下平移4个单位
9．在下列说法中：①△ABC在平移过程中，对应线段一定相等；②△ABC在平移过程中，对应线段一定平行；③△ABC在平移过程中，周长保持不变；④△ABC在平移过程中，对应边中点所连线段的长等于平移的距离；⑤△ABC在平移过程中，面积不变，其中正确的有（　　）
A．①②③④ B．①②③④⑤ C．①②③⑤ D．①③④⑤
10．如图，将直线l1沿着AB的方向平移得到直线l2，若∠1=50°，则∠2的度数是（　　）
A．40° B．50° C．90° D．130°
二．填空题（共8小题）
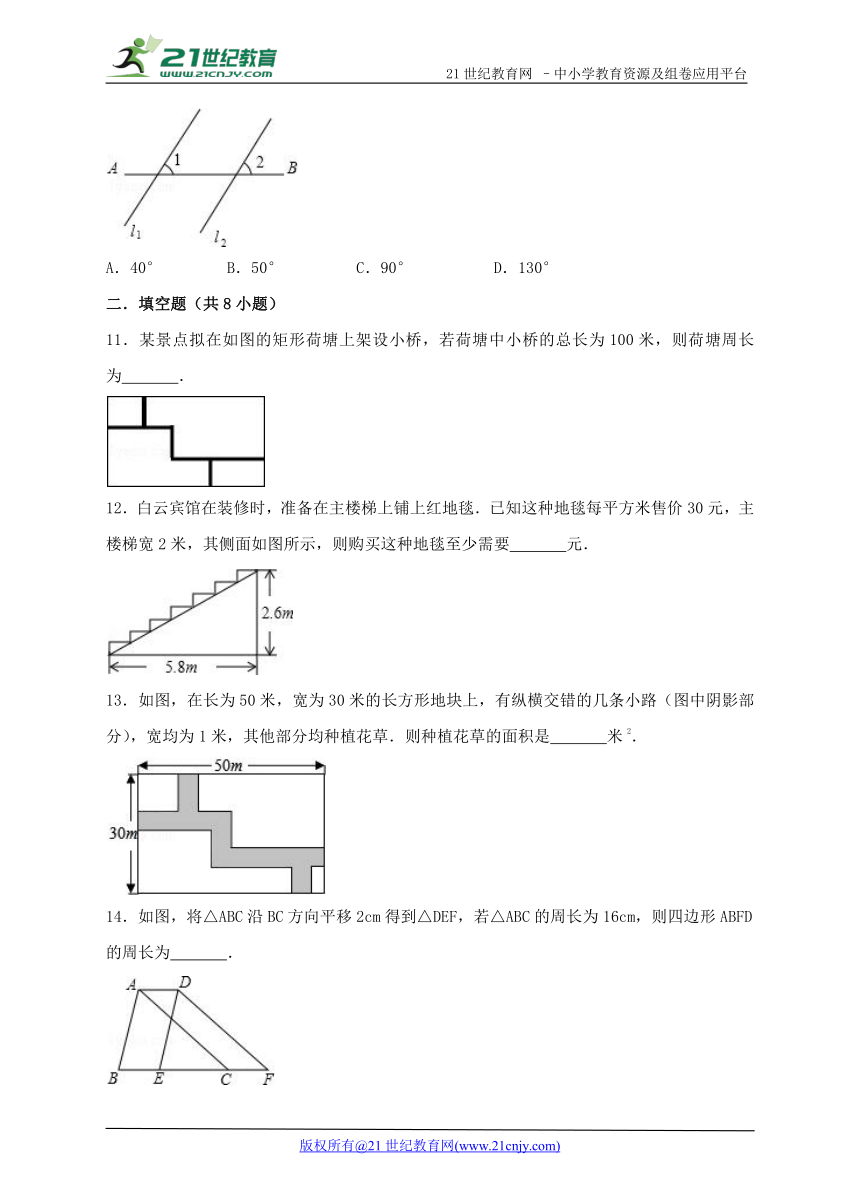
11．某景点拟在如图的矩形荷塘上架设小桥，若荷塘中小桥的总长为100米，则荷塘周长为　 　．
12．白云宾馆在装修时，准备在主楼梯上铺上红地毯．已知这种地毯每平方米售价30元，主楼梯宽2米，其侧面如图所示，则购买这种地毯至少需要　 　元．
13．如图，在长为50米，宽为30米的长方形地块上，有纵横交错的几条小路（图中阴影部分），宽均为1米，其他部分均种植花草．则种植花草的面积是　 　米2．
14．如图，将△ABC沿BC方向平移2cm得到△DEF，若△ABC的周长为16cm，则四边形ABFD的周长为　 　．
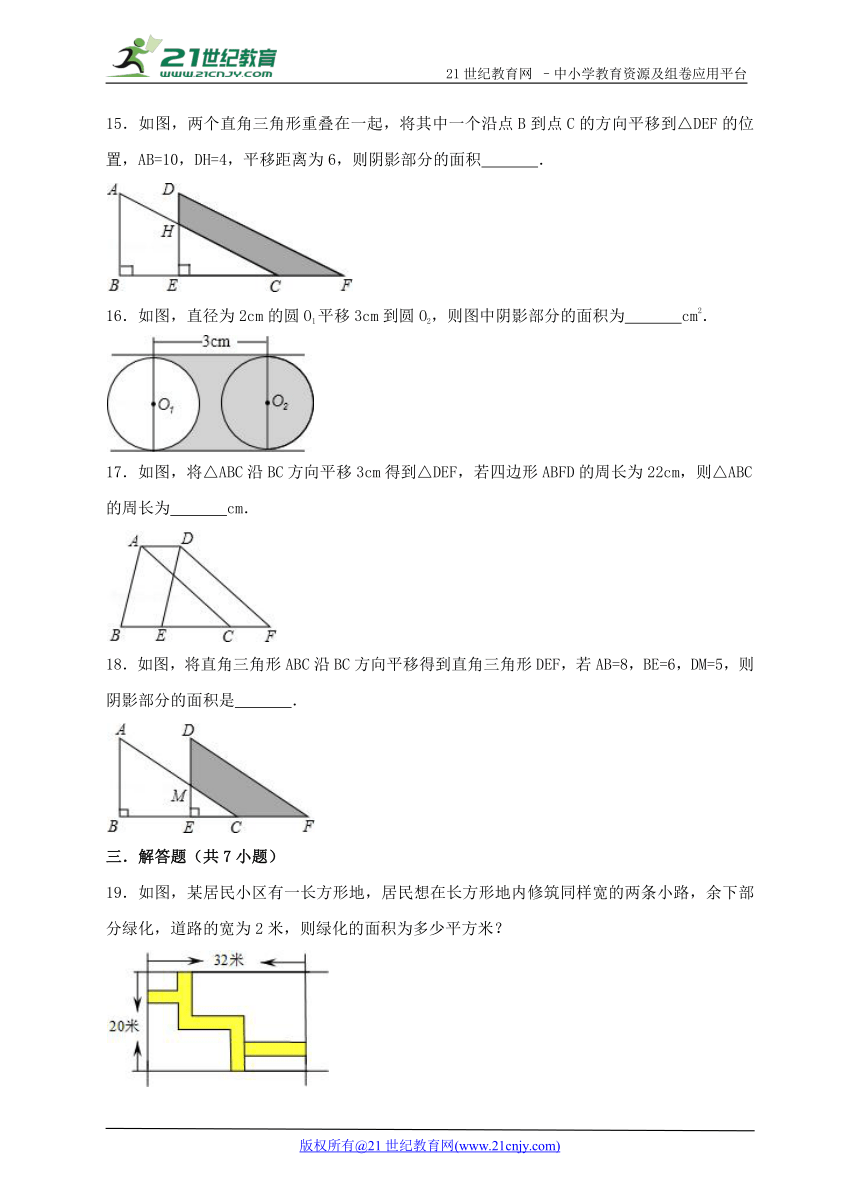
15．如图，两个直角三角形重叠在一起，将其中一个沿点B到点C的方向平移到△DEF的位置，AB=10，DH=4，平移距离为6，则阴影部分的面积　 　．
16．如图，直径为2cm的圆O1平移3cm到圆O2，则图中阴影部分的面积为　 　cm2．
17．如图，将△ABC沿BC方向平移3cm得到△DEF，若四边形ABFD的周长为22cm，则△ABC的周长为　 　cm．
18．如图，将直角三角形ABC沿BC方向平移得到直角三角形DEF，若AB=8，BE=6，DM=5，则阴影部分的面积是　 　．
三．解答题（共7小题）
19．如图，某居民小区有一长方形地，居民想在长方形地内修筑同样宽的两条小路，余下部分绿化，道路的宽为2米，则绿化的面积为多少平方米？
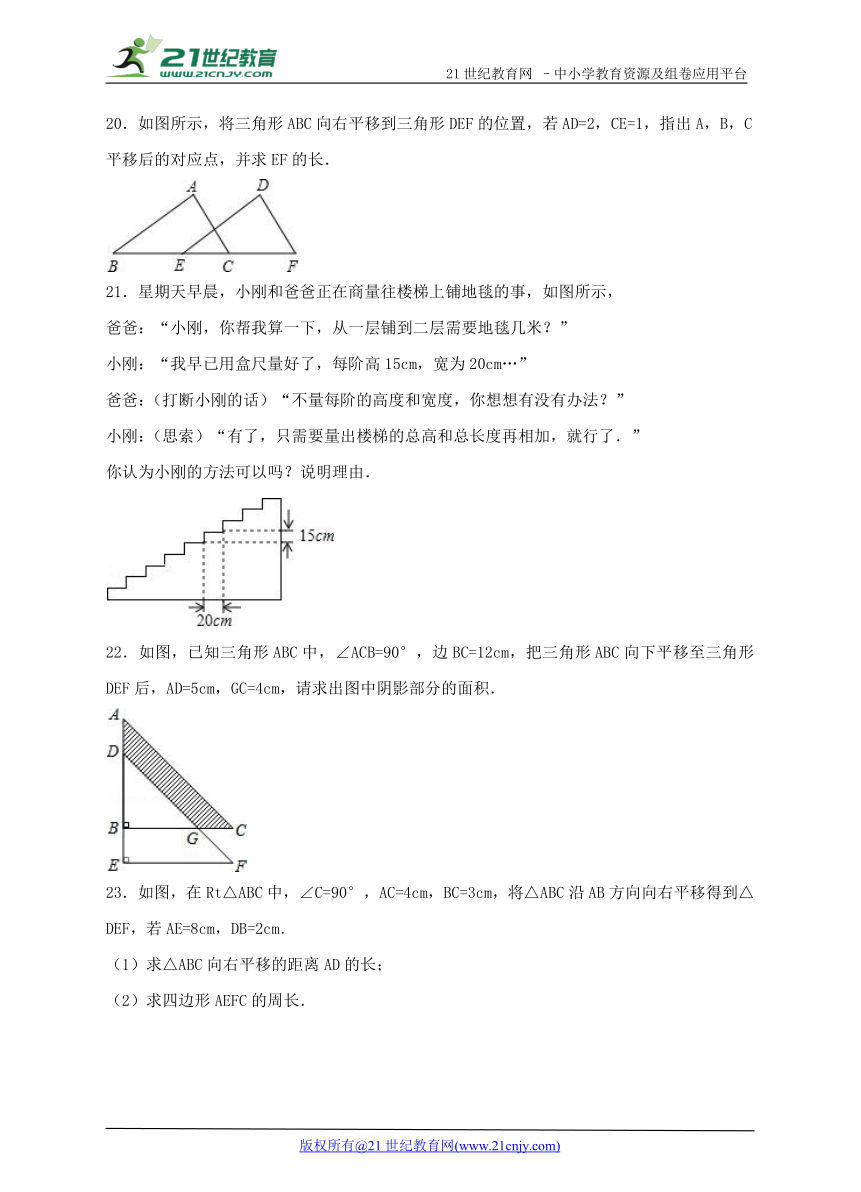
20．如图所示，将三角形ABC向右平移到三角形DEF的位置，若AD=2，CE=1，指出A，B，C平移后的对应点，并求EF的长．
21．星期天早晨，小刚和爸爸正在商量往楼梯上铺地毯的事，如图所示，
爸爸：“小刚，你帮我算一下，从一层铺到二层需要地毯几米？”
小刚：“我早已用盒尺量好了，每阶高15cm，宽为20cm…”
爸爸：（打断小刚的话）“不量每阶的高度和宽度，你想想有没有办法？”
小刚：（思索）“有了，只需要量出楼梯的总高和总长度再相加，就行了．”
你认为小刚的方法可以吗？说明理由．
22．如图，已知三角形ABC中，∠ACB=90°，边BC=12cm，把三角形ABC向下平移至三角形DEF后，AD=5cm，GC=4cm，请求出图中阴影部分的面积．
23．如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=3cm，将△ABC沿AB方向向右平移得到△DEF，若AE=8cm，DB=2cm．
（1）求△ABC向右平移的距离AD的长；
（2）求四边形AEFC的周长．
24．（1）图①是将线段AB向右平移1个单位长度，图②是将线段AB折一下再向右平移1个单位长度，请在图③中画出一条有两个折点的折线向右平移1个单位长度的图形．
（2）若长方形的长为a，宽为b，请分别写出三个图形中除去阴影部分后剩余部分的面积．
（3）如图④，在宽为10m，长为40m的长方形菜地上有一条弯曲的小路，小路宽为1m，求这块菜地的面积．
25．现有一张台阶的图纸，如图所示，请按要求回答问题：
（1）如果需要在台阶上铺红地毯，需要铺多长的红地毯？
（2）如果红地毯的宽度为2米，需要多大面积的红地毯？
（3）如果红地毯的售价为2元/平方米（1平方米两元钱），需要花多少钱购置红地毯？
　
参考答案与试题解析
　
一．选择题（共10小题）
1．下列生活中的各个现象，属于平移变换现象的是（　　）
A．拉开抽屉 B．用放大镜看文字
C．时钟上分针的运动 D．你和平面镜中的像
【分析】根据平移的定义直接判断即可．
解：A、是平移；
B、大小发生变化，不是平移；
C、是旋转；
D、你和平面镜中的像不是平移，是轴对称．
故选A．
　
2．下列哪个图形是由如图平移得到的（　　）
A． B． C． D．
【分析】根据平移的性质，结合图形，对选项进行一一分析，排除错误答案．
解：A、图形属于旋转得到，故错误；
B、图形属于旋转得到，故错误；
C、图形的形状和大小没的变化，符合平移性质，故正确；
D、图形属于旋转得到，故错误．
故选C．
　
3．下列图形中，不能通过其中一个四边形平移得到的是（　　）
A． B． C． D．
【分析】根据平移与旋转的性质得出．
解：A、能通过其中一个四边形平移得到，错误；
B、能通过其中一个四边形平移得到，错误；
C、能通过其中一个四边形平移得到，错误；
D、不能通过其中一个四边形平移得到，需要一个四边形旋转得到，正确．
故选D．
　
4．下列现象属于平移的有（　　）个．
①气筒活塞的往复运动，②荡秋千，③钟摆的摆动，④转动的门．
A．2 B．3 C．1 D．4
【分析】根据平移的定义即可作出判断．
解：①气筒活塞的往复运动是平移，②荡秋千不是平移，③钟摆的摆动不是平移，④转动的门不是平移，
故选C
　
5．如图，△DEF是由△ABC通过平移得到，且点B，E，C，F在同一条直线上．若BF=14，EC=6．则BE的长度是（　　）
A．2 B．4 C．5 D．3
【分析】根据平移的性质可得BE=CF，然后列式其解即可．
解：∵△DEF是由△ABC通过平移得到，
∴BE=CF，
∴BE=（BF﹣EC），
∵BF=14，EC=6，
∴BE=（14﹣6）=4．
故选B．
　
6．下列说法不正确的是（　　）
A．把一个图形平移到一个确定位置，大小形状都不变
B．在平移图形的过程中，图形上的各点坐标发生同样的变化
C．在平移过程中图形上的个别点的坐标不变
D．平移后的两个图形的对应角相等，对应边相等，对应边平行或共线
【分析】平移的基本性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．对各个选项进行判断．
解：把一个图形平移到一个确定位置，大小形状都不变，在平移图形的过程中，图形上的各点坐标发生同样的变化，平移后的两个图形的对应角相等，对应边相等，对应边平行或共线，都可由平移基本性质得到．故A、B、D正确．
在平移过程中图形上的所有点的坐标都改变．故C错误．故选C．
　
7．如图，四边形EFGH是由四边形ABCD平移得到的，已知AD=5，∠B=70°，则（　　）
A．FG=5，∠G=70° B．EH=5，∠F=70° C．EF=5，∠F=70° D．EF=5，∠E=70°
【分析】经过平移，对应线段平行（或共线）且相等，对应角相等，对应点所连接的线段平行且相等．
解：在四边形EFGH，EH是AD的对应边，∠F是∠B的对应角，
∵AD=5，∠B=70°，故EH=5，∠F=70°．
故选B．
　
8．如图，在6×6方格中有两个涂有阴影的图形M、N，①中的图形M平移后位置如②所示，以下对图形M的平移方法叙述正确的是（　　）
A．向右平移2个单位，向下平移3个单位
B．向右平移1个单位，向下平移3个单位
C．向右平移1个单位，向下平移4个单位
D．向右平移2个单位，向下平移4个单位
【分析】根据平移前后图形M中某一个对应顶点的位置变化情况进行判断即可．
解：根据图形M平移前后对应点的位置变化可知，需要向右平移1个单位，向下平移3个单位．
故选（B）
　
9．在下列说法中：①△ABC在平移过程中，对应线段一定相等；②△ABC在平移过程中，对应线段一定平行；③△ABC在平移过程中，周长保持不变；④△ABC在平移过程中，对应边中点所连线段的长等于平移的距离；⑤△ABC在平移过程中，面积不变，其中正确的有（　　）
A．①②③④ B．①②③④⑤ C．①②③⑤ D．①③④⑤
【分析】根据图形平移的基本性质，对①、②、③、④、⑤逐一进行判断，验证其是否正确．
解：①∵平移不改变图形的大小，∴△ABC在平移过程中，对应线段一定相等，故正确；
②∵经过平移，对应线段所在的直线共线或平行，∴对应线段一定平行错误；
③∵平移不改变图形的形状和大小，∴△ABC在平移过程中，周长不变，故正确；
④∵经过平移，对应点所连的线段平行且相等，∴△ABC在平移过程中，对应边中点所连线段的长等于平移的距离，正确；
⑤∵移不改变图形的形状和大小且对应角相等，∴△ABC在平移过程中，面积不变，故正确；
∴①、③、④、⑤都符合平移的基本性质，都正确．
故选D．
　
10．如图，将直线l1沿着AB的方向平移得到直线l2，若∠1=50°，则∠2的度数是（　　）
A．40° B．50° C．90° D．130°
【分析】根据平移的性质得出l1∥l2，进而得出∠2的度数．
解：∵将直线l1沿着AB的方向平移得到直线l2，
∴l1∥l2，
∵∠1=50°，
∴∠2的度数是50°．
故选：B．
　
二．填空题（共8小题）
11．某景点拟在如图的矩形荷塘上架设小桥，若荷塘中小桥的总长为100米，则荷塘周长为　200m　．
【分析】根据图形得出荷塘中小桥的总长为矩形的长与宽的和，进而得出答案．
解：∵荷塘中小桥的总长为100米，
∴荷塘周长为：2×100=200（m）
故答案为：200m．
　
12．白云宾馆在装修时，准备在主楼梯上铺上红地毯．已知这种地毯每平方米售价30元，主楼梯宽2米，其侧面如图所示，则购买这种地毯至少需要　504　元．
【分析】根据题意，结合图形，先把楼梯的横竖向上向右平移，构成一个矩形，再求得其面积，则购买地毯的钱数可求．
解：如图，利用平移线段，把楼梯的横竖向上向右平移，构成一个矩形，长宽分别为5.8米，2.6米，
即可得地毯的长度为2.6+5.8=8.4（米），地毯的面积为8.4×2=16.8（平方米），
故买地毯至少需要16.8×30=504（元）．
故答案为：504．
　
13．如图，在长为50米，宽为30米的长方形地块上，有纵横交错的几条小路（图中阴影部分），宽均为1米，其他部分均种植花草．则种植花草的面积是　1421　米2．
【分析】可以根据平移的性质，此小路相当于一条横向长为50米与一条纵向长为30米的小路，种植花草的面积=总面积﹣小路的面积+小路交叉处的面积，计算即可．
解：根据题意，小路的面积相当于横向与纵向的两条小路，
种植花草的面积=（50﹣1）（30﹣1）=1421m2．
故答案为：1421．
　
14．如图，将△ABC沿BC方向平移2cm得到△DEF，若△ABC的周长为16cm，则四边形ABFD的周长为　20cm　．
【分析】先根据平移的性质得到CF=AD=2cm，AC=DF，而AB+BC+AC=16cm，则四边形ABFD的周长=AB+BC+CF+DF+AD，然后利用整体代入的方法计算即可．
解：∵△ABC沿BC方向平移2cm得到△DEF，
∴CF=AD=2cm，AC=DF，
∵△ABC的周长为16cm，
∴AB+BC+AC=16cm，
∴四边形ABFD的周长=AB+BC+CF+DF+AD
=AB+BC+AC+CF+AD
=16cm+2cm+2cm
=20cm．
故答案为：20cm．
　
15．如图，两个直角三角形重叠在一起，将其中一个沿点B到点C的方向平移到△DEF的位置，AB=10，DH=4，平移距离为6，则阴影部分的面积　48　．
【分析】根据平移的性质可知：AB=DE，BE=CF；由此可求出EH和CF的长．由于CH∥DF，可得出△ECH∽△EFD，根据相似三角形的对应边成比例，可求出EC的长．已知了EH、EC，DE、EF的长，即可求出△ECH和△EFD的面积，进而可求出阴影部分的面积．
解：根据题意得，DE=AB=10；BE=CF=6；CH∥DF．
∴EH=10﹣4=6；
EH：HD=EC：CF，
即 6：4=EC：6，
∴EC=9．
∴S△EFD=×10×（9+6）=75；
S△ECH=×6×9=27．
∴S阴影部分=75﹣27=48．
故答案为48．
　
16．如图，直径为2cm的圆O1平移3cm到圆O2，则图中阴影部分的面积为　6　cm2．
【分析】由平移的性质知，⊙O1与⊙O2是全等的，所以图中的阴影部分的面积与图中的矩形的面积是相等的，故图中阴影部分面积可求．
解：∵⊙O1平移3cm到⊙O2
∴⊙O1与⊙O2全等
∴图中的阴影部分的面积=图中的矩形的面积
∴2×3=6cm2
∴图中阴影部分面积为6cm2．
故答案为：6．
　
17．如图，将△ABC沿BC方向平移3cm得到△DEF，若四边形ABFD的周长为22cm，则△ABC的周长为　16　cm．
【分析】先利用平移的性质得AC=DF，AD=CF=3，然后利用AB+BC+CF+DF+AD=22得到AB+BC+AC=26，从而得到△ABC的周长为26cm．
解：∵△ABC沿BC方向平移3cm得到△DEF，
∴AC=DF，AD=CF=3，
∵四边形ABFD的周长是22cm，
即AB+BC+CF+DF+AD=22，
∴AB+BC+AC+3+3=22，
即AB+BC+AC=16，
∴△ABC的周长为16cm．
故答案为16．
　
18．如图，将直角三角形ABC沿BC方向平移得到直角三角形DEF，若AB=8，BE=6，DM=5，则阴影部分的面积是　33　．
【分析】根据平移的性质可得DE=AB，然后求出ME，再求出S阴影=S梯形ABEM，然后根据梯形的面积公式列式计算即可得解．
解：∵直角△ABC沿BC方向平移得到直角△DEF，
∴DE=AB=8，
∵DM=5，
∴ME=DE﹣DM=8﹣5=3，
由平移可得：
S阴影=S△DEF﹣S△MEC
=S△ABC﹣S△MEC
=S梯形ABEM
=×（3+8）×6，
=33．
故答案为：33．
　
三．解答题（共7小题）
19．如图，某居民小区有一长方形地，居民想在长方形地内修筑同样宽的两条小路，余下部分绿化，道路的宽为2米，则绿化的面积为多少平方米？
【分析】平移后可得道路的长和宽，再利用矩形的面积公式进行计算即可．
解：平移后得绿化部分宽为（20﹣2）米，长为（32﹣2）米，
面积为（20﹣2）×（32﹣2）=18×30=540（平方米）．
答：则绿化的面积为540平方米．
　
20．如图所示，将三角形ABC向右平移到三角形DEF的位置，若AD=2，CE=1，指出A，B，C平移后的对应点，并求EF的长．
【分析】根据△DEF由△ABC平移而成，所以A，B，C平移后的对应点分别是D，E，F，再根据AD=2可知CF=2，由EF=CE+CF即可得出结论．
解：∵△DEF由△ABC平移而成，
∴A，B，C平移后的对应点分别是D，E，F，
∵AD=2，
∴CF=2，
∴EF=CE+CF=1+2=3．
　
21．星期天早晨，小刚和爸爸正在商量往楼梯上铺地毯的事，如图所示，
爸爸：“小刚，你帮我算一下，从一层铺到二层需要地毯几米？”
小刚：“我早已用盒尺量好了，每阶高15cm，宽为20cm…”
爸爸：（打断小刚的话）“不量每阶的高度和宽度，你想想有没有办法？”
小刚：（思索）“有了，只需要量出楼梯的总高和总长度再相加，就行了．”
你认为小刚的方法可以吗？说明理由．
【分析】根据平移可得地毯的总长度=AB+CB．
解：可以，
如图所示：根据图示可得：地毯的总长度=AB+CB=15×9+20×9=（15+20）×9=315（cm）．
　
22．如图，已知三角形ABC中，∠ACB=90°，边BC=12cm，把三角形ABC向下平移至三角形DEF后，AD=5cm，GC=4cm，请求出图中阴影部分的面积．
【分析】根据平移变化只改变图形的位置不改变图形的形状可得AB=DE，△ABC≌△DEF，然后求出BG，再求出梯形BGEF的面积即为阴影部分的面积．
解：∵Rt△ABC沿BC方向平移得到Rt△DEF，
∴BC=EF=12cm，△ABC≌△DEF，
∴阴影部分面积=梯形BGEF的面积，
∵GC=4cm，
∴BG=12﹣4=8cm，
∴阴影部分面积=×（8+12）×5=50cm2．
故答案为：50．
　
23．如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=3cm，将△ABC沿AB方向向右平移得到△DEF，若AE=8cm，DB=2cm．
（1）求△ABC向右平移的距离AD的长；
（2）求四边形AEFC的周长．
【分析】（1）根据平移的性质可得AD=BE=CF，BC=EF=3cm，然后根据AE、BD的长度求解即可；
（2）根据平移的性质可得EF=BC，CF=AD，然后根据四边形的周长的定义列式计算即可得解．
解：（1）∵△ABC沿AB方向向右平移得到△DEF，
∴AD=BE=CF，BC=EF=3cm，
∵AE=8cm，DB=2cm，
∴AD=BE=CF==3cm；
（2）四边形AEFC的周长=AE+EF+CF+AC=8+3+3+4=18cm．
　
24．（1）图①是将线段AB向右平移1个单位长度，图②是将线段AB折一下再向右平移1个单位长度，请在图③中画出一条有两个折点的折线向右平移1个单位长度的图形．
（2）若长方形的长为a，宽为b，请分别写出三个图形中除去阴影部分后剩余部分的面积．
（3）如图④，在宽为10m，长为40m的长方形菜地上有一条弯曲的小路，小路宽为1m，求这块菜地的面积．
【分析】（1）根据两个折点，可得小路是三个平行四边形；
（2）根据路的形状是矩形，可得路的面积，根据面积的和差，可得答案；
（3）根据等底等高的面积相等，可得路的面积，根据面积的和差，可得答案．
解：（1）如图：
；
（2）三个图形中除去阴影部分后剩余部分的面积：①ab﹣b；②ab﹣b；③ab﹣b；
（3）40×10﹣10×1=390（m2）．
答：这块菜地的面积是390m2．
　
25．现有一张台阶的图纸，如图所示，请按要求回答问题：
（1）如果需要在台阶上铺红地毯，需要铺多长的红地毯？
（2）如果红地毯的宽度为2米，需要多大面积的红地毯？
（3）如果红地毯的售价为2元/平方米（1平方米两元钱），需要花多少钱购置红地毯？
【分析】（1）地毯的长是6+8；
（2）地毯的面积=地毯的长×宽；
（3）地毯的价钱=面积×销售单价
解：（1）地毯的长是：6+8=14（米）；
（2）14×2=28（平方米）；
（3）2×28=56（元）．
　
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
版权所有@21世纪教育网(www.21cnjy.com)