3.2 单项式的乘法(1)同步练习
图片预览


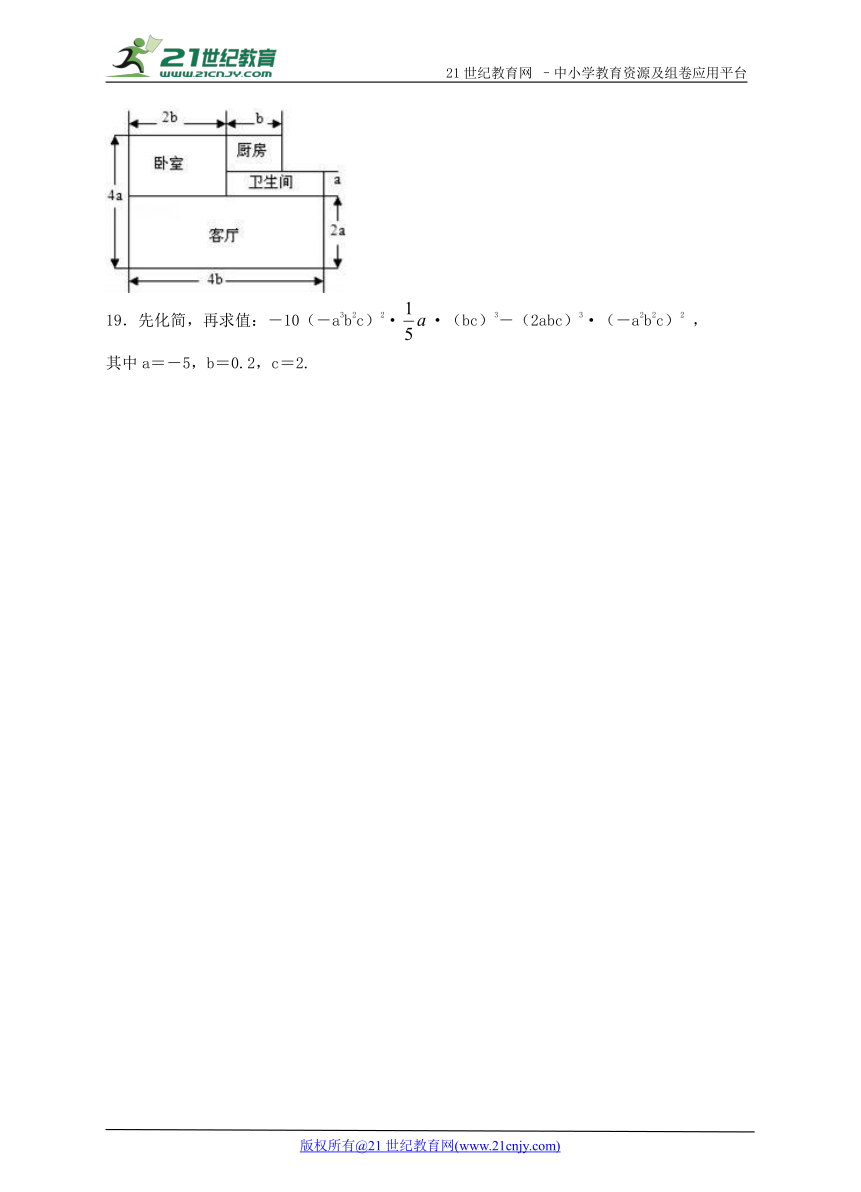

文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
3.2单项式的乘法(1)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
运算性质:单项式与单项式相乘,把他们的系数,相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
注意:①在计算时,应先进行符号运算,积的系数等于各因式系数的积;②注意按顺序运算;③不要丢掉只在一个单项式里含有的字母因式;④此性质对于多个单项式相乘仍然成立.
基础知识和能力拓展精练
一、选择题
1.-3ab2·(-2a2b3)2的计算结果是( )
A. B. C. D.
2.若等式2a□a=2a2一定成立,则□内的运算符号为( )
A.+ B.﹣ C.× D.÷
3.在电子显微镜下测得一个圆球体细胞的直径是5×10,个这样的细胞排成的细胞链的长是( )
A. B. C. D.
4.计算的结果是( )
A. B. C. D.
5.计算的结果是( ).
A. B. C. D.
6.如果单项式-2xa-2by2a+b与x3y8b是同类项,那么这两个单项式的积是( )
A. -2x6y16 B. -2x6y32 C. -2x3y8 D. -4x6y16
7.下列运算正确的是( )
A. (-2ab)·(-3ab)3=-54a4b4 B. 5x2·(3x3)2=15x12
C. (-0.1b)·(-10b2)3=-b7 D. (2×10n) =102n
8.下列计算错误的是( )
A. B.
C. D.
9.N是一个单项式,且N·(-2x2y)=-3ax2y2,则N等于( )
A.ay B.-3ay C.-xy D.axy
二、填空题
10.-3(a-b)2·[2(a-b)3]·[ (a-b)]=________.
11.一个三角形的底为,高为,则它的面积为________.
12.计算: ________________________.
13.已知单项式与的积为,那么_________.
14.一个长方体的长为2×103cm,宽为1.5×102cm,高为1.2×102cm,则它的体积是 ______ cm3.
三、解答题
15.计算:①(-5ab2x)·(-a2bx3y) ②(-2×103)3×(-4×108)2
16.光的速度是每秒钟3×105千米,有一颗恒星发射的光要10年才能到达地球,若一年以3.1×107秒计算,这颗恒星离地球有多少千米
17.若(am+1bn+2)(a2n-1b2n)=a5b3,求m+n的值.
18.李叔叔刚分到一套新房,其结构如图,他打算除卧室外,其余部分铺地砖,则
(1)至少需要多少平方米地砖?
(2)如果铺的这种地砖的价格75元/米2,那么李叔叔至少需要花多少元钱?
19.先化简,再求值:―10(―a3b2c)2··(bc)3―(2abc)3·(―a2b2c)2 ,
其中a=―5,b=0.2,c=2.
参考答案
1.B
【解析】 ;
故选B。
2.C
【解析】
试题分析:由2a a=2a2,可知等式2a□a=2a2一定成立,则□内的运算符号为×,
故选C.
考点:单项式乘单项式
3.B
【解析】
试题分析:因为,所以选:B.
考点:同底数幂的运算.
4.C
【解析】原式=48×108=4.8×109.
故选C.
5.B
【解析】.所以选B.
6.B
【解析】由同类项的定义得,a-2b=3,2a+b=8b,联立这两个方程解得a=7,b=2,
所以-2x3y16·x3y16=-2x6y32.
故选B.
7.D
【解析】解:A. 原式=54a4b4,故A错误;
B.原式=45x8,故B错误;
C. 原式=100b7,故C错误;
D.正确.
故选D.
8.B
【解析】选项A,原式=;选项B,原式=;选项C,原式= ;选项D,原式=,四个选项中只有选项B错误,故选B.
9.A
【解析】
试题分析:根据单项式乘单项式法则即可得到结果。
∵N·(-2x2y)=-3ax2y2,
∴N= SHAPE \* MERGEFORMAT EMBED \* MERGEFORMAT ay,
故选A.
考点:本题考查的是单项式乘单项式
点评:解答本题的关键是熟练掌握单项式乘以单项式的法则,系数与系数相乘,相同字母与相同字母相乘,对于只在一个单项式里出现的字母,则连同它的指数作为积的一个因式.
10.-4(a-b)6
【解析】原式 .
【点睛】本题考查了单项式的乘法.单项式与单项式的乘法法则是,把它们的系数相乘,字母部分的同底数的幂分别相乘,对于只在一个单项式里含有的字母,连同它的指数作为积的一个因式.
11.
【解析】由三角形的面积公式得, .
12.6x4y4
【解析】试题解析:根据单项式乘单项式的法则得:(-2x2y) (-3x2y3)=6x4y4.
13.-20
【解析】试题解析:由题意可知:3x2y3×(-5x2y2)=mx4yn,
∴m=-15,n=5,
∴m-n=-20.
14.3.6×107
【解析】长方体的体积是:2×103×1.5×102×1.2×102=3.6×107.
故答案为:3.6×107.
15.①a3b3x4y;② -1.28×1027
【解析】试题分析:(1)根据单项式的乘法法则计算即可;(2)先按照积的乘方法则计算,然后仿照单项式的乘法法则计算.
①原式=
②原式=-2×(-4)× × =8×
16.9.3×1013
【解析】试题分析:根据路程=速度×时间解答即可.
3×105×3.1×107×10=9.3×1013(千米)
【点睛】科学计数法的乘法按照单项式的乘法计算,最后的结果仍然用科学计数法表示.
17.
【解析】试题分析:把(am+1bn+2)(a2n-1b2n)根据单项式的乘法法则化简,得到am+2nb3n+2=a5b3,两边比较可得m+2n=5,3n+2=3,求出m,n的值,代入m+n到计算即可.
解:(am+1bn+2)(a2n-1b2n)=am+1×a2n-1×bn+2×b2n=am+1+2n-1×bn+2+2n=am+2nb3n+2=a5b3.所以m+2n=5,3n+2=3,解得n=,m=,所以m+n=.
18.(1)11ab; (2)825ab元
【解析】(1)11ab;
(2)825ab元
【试题分析】
分别计算出厨房,卫生间,客厅的面积,然后相加就是所需要的地砖的面积;
(2)所需要的钱=75×地砖的面积.
【点睛】本题属于求解不规则多边形的面积的题目,求面积有以下几种方法:
(1)补形法:计算某个图形的面积,如果它的面积难以直接求出,那么就设法把它补成面积较容易计算的图形;
(2)分割法:把应求部分的图形分割成若干份规则的图形,求它们的面积和;
19.―10 a7b7c5,320.
【解析】试题分析:本题考查了单项式的混合运算,与有理数的混合运算顺序一样,先算乘方,再算乘法,最后合并同类项.
原式=―2a7b7c5―8a7b7c5=―10 a7b7c5. 当 a=―5,b=0.2,c=2时,
原式=―10×(―5)7×(0.2)7×25=320.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
3.2单项式的乘法(1)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
运算性质:单项式与单项式相乘,把他们的系数,相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
注意:①在计算时,应先进行符号运算,积的系数等于各因式系数的积;②注意按顺序运算;③不要丢掉只在一个单项式里含有的字母因式;④此性质对于多个单项式相乘仍然成立.
基础知识和能力拓展精练
一、选择题
1.-3ab2·(-2a2b3)2的计算结果是( )
A. B. C. D.
2.若等式2a□a=2a2一定成立,则□内的运算符号为( )
A.+ B.﹣ C.× D.÷
3.在电子显微镜下测得一个圆球体细胞的直径是5×10,个这样的细胞排成的细胞链的长是( )
A. B. C. D.
4.计算的结果是( )
A. B. C. D.
5.计算的结果是( ).
A. B. C. D.
6.如果单项式-2xa-2by2a+b与x3y8b是同类项,那么这两个单项式的积是( )
A. -2x6y16 B. -2x6y32 C. -2x3y8 D. -4x6y16
7.下列运算正确的是( )
A. (-2ab)·(-3ab)3=-54a4b4 B. 5x2·(3x3)2=15x12
C. (-0.1b)·(-10b2)3=-b7 D. (2×10n) =102n
8.下列计算错误的是( )
A. B.
C. D.
9.N是一个单项式,且N·(-2x2y)=-3ax2y2,则N等于( )
A.ay B.-3ay C.-xy D.axy
二、填空题
10.-3(a-b)2·[2(a-b)3]·[ (a-b)]=________.
11.一个三角形的底为,高为,则它的面积为________.
12.计算: ________________________.
13.已知单项式与的积为,那么_________.
14.一个长方体的长为2×103cm,宽为1.5×102cm,高为1.2×102cm,则它的体积是 ______ cm3.
三、解答题
15.计算:①(-5ab2x)·(-a2bx3y) ②(-2×103)3×(-4×108)2
16.光的速度是每秒钟3×105千米,有一颗恒星发射的光要10年才能到达地球,若一年以3.1×107秒计算,这颗恒星离地球有多少千米
17.若(am+1bn+2)(a2n-1b2n)=a5b3,求m+n的值.
18.李叔叔刚分到一套新房,其结构如图,他打算除卧室外,其余部分铺地砖,则
(1)至少需要多少平方米地砖?
(2)如果铺的这种地砖的价格75元/米2,那么李叔叔至少需要花多少元钱?
19.先化简,再求值:―10(―a3b2c)2··(bc)3―(2abc)3·(―a2b2c)2 ,
其中a=―5,b=0.2,c=2.
参考答案
1.B
【解析】 ;
故选B。
2.C
【解析】
试题分析:由2a a=2a2,可知等式2a□a=2a2一定成立,则□内的运算符号为×,
故选C.
考点:单项式乘单项式
3.B
【解析】
试题分析:因为,所以选:B.
考点:同底数幂的运算.
4.C
【解析】原式=48×108=4.8×109.
故选C.
5.B
【解析】.所以选B.
6.B
【解析】由同类项的定义得,a-2b=3,2a+b=8b,联立这两个方程解得a=7,b=2,
所以-2x3y16·x3y16=-2x6y32.
故选B.
7.D
【解析】解:A. 原式=54a4b4,故A错误;
B.原式=45x8,故B错误;
C. 原式=100b7,故C错误;
D.正确.
故选D.
8.B
【解析】选项A,原式=;选项B,原式=;选项C,原式= ;选项D,原式=,四个选项中只有选项B错误,故选B.
9.A
【解析】
试题分析:根据单项式乘单项式法则即可得到结果。
∵N·(-2x2y)=-3ax2y2,
∴N= SHAPE \* MERGEFORMAT EMBED \* MERGEFORMAT ay,
故选A.
考点:本题考查的是单项式乘单项式
点评:解答本题的关键是熟练掌握单项式乘以单项式的法则,系数与系数相乘,相同字母与相同字母相乘,对于只在一个单项式里出现的字母,则连同它的指数作为积的一个因式.
10.-4(a-b)6
【解析】原式 .
【点睛】本题考查了单项式的乘法.单项式与单项式的乘法法则是,把它们的系数相乘,字母部分的同底数的幂分别相乘,对于只在一个单项式里含有的字母,连同它的指数作为积的一个因式.
11.
【解析】由三角形的面积公式得, .
12.6x4y4
【解析】试题解析:根据单项式乘单项式的法则得:(-2x2y) (-3x2y3)=6x4y4.
13.-20
【解析】试题解析:由题意可知:3x2y3×(-5x2y2)=mx4yn,
∴m=-15,n=5,
∴m-n=-20.
14.3.6×107
【解析】长方体的体积是:2×103×1.5×102×1.2×102=3.6×107.
故答案为:3.6×107.
15.①a3b3x4y;② -1.28×1027
【解析】试题分析:(1)根据单项式的乘法法则计算即可;(2)先按照积的乘方法则计算,然后仿照单项式的乘法法则计算.
①原式=
②原式=-2×(-4)× × =8×
16.9.3×1013
【解析】试题分析:根据路程=速度×时间解答即可.
3×105×3.1×107×10=9.3×1013(千米)
【点睛】科学计数法的乘法按照单项式的乘法计算,最后的结果仍然用科学计数法表示.
17.
【解析】试题分析:把(am+1bn+2)(a2n-1b2n)根据单项式的乘法法则化简,得到am+2nb3n+2=a5b3,两边比较可得m+2n=5,3n+2=3,求出m,n的值,代入m+n到计算即可.
解:(am+1bn+2)(a2n-1b2n)=am+1×a2n-1×bn+2×b2n=am+1+2n-1×bn+2+2n=am+2nb3n+2=a5b3.所以m+2n=5,3n+2=3,解得n=,m=,所以m+n=.
18.(1)11ab; (2)825ab元
【解析】(1)11ab;
(2)825ab元
【试题分析】
分别计算出厨房,卫生间,客厅的面积,然后相加就是所需要的地砖的面积;
(2)所需要的钱=75×地砖的面积.
【点睛】本题属于求解不规则多边形的面积的题目,求面积有以下几种方法:
(1)补形法:计算某个图形的面积,如果它的面积难以直接求出,那么就设法把它补成面积较容易计算的图形;
(2)分割法:把应求部分的图形分割成若干份规则的图形,求它们的面积和;
19.―10 a7b7c5,320.
【解析】试题分析:本题考查了单项式的混合运算,与有理数的混合运算顺序一样,先算乘方,再算乘法,最后合并同类项.
原式=―2a7b7c5―8a7b7c5=―10 a7b7c5. 当 a=―5,b=0.2,c=2时,
原式=―10×(―5)7×(0.2)7×25=320.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
