浙教版数学七年级下册同步练习:1.1 平行线
文档属性
| 名称 | 浙教版数学七年级下册同步练习:1.1 平行线 |  | |
| 格式 | zip | ||
| 文件大小 | 189.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-06 14:21:17 | ||
图片预览

文档简介
第1章 平行线
1.1 平行线
课堂笔记
1. 在 ,不相交的两条直线叫做平行线.
2. 经过直线外一点,有且只有 直线与这条直线平行.
分层训练
A组 基础训练
1. 在同一平面内,两条不重合的直线的位置关系可能是( )
A. 平行或相交 B. 垂直或相交
C. 垂直或平行 D. 平行、垂直或相交
2. 在同一平面内有三条直线,若其中有且只有两条直线互相平行,则它们交点的个数为( )
A. 0 B. 1 C. 2 D. 3
3. 已知∠AOB与其内部任意一点P,若过点P画一条直线与OA平行,那么这样的直线( )
A. 有且只有一条 B. 有两条 C. 有无数条 D. 不存在
4. 下列说法错误的是( )
A. 在同一平面内,直线a∥b,若c与a相交,则b与c也相交
B. 在同一平面内,直线a与b相交,c与a相交,则b∥c
C. 在同一平面内,两条不平行的直线是相交线
D. 直线AB与CD平行,则AB上所有点都在CD的同侧
5. 如图,将一张长方形纸对折两次,产生的折痕与折痕之间的位置关系是( )
A. 平行 B. 垂直 C. 平行或垂直 D. 无法确定
6. 在如图所示的直三棱柱中,互相平行的棱有( )
A. 3对 B. 4对 C. 5对 D. 6对
7. 在同一平面内,若两条直线相交,则公共点的个数是 ;若两条直线平行,则公共点的个数是 .21教育网
8. 体育教师在操场上画100m的直跑道,如果画6条跑道,需要画 条线段,这些线段的位置关系是 .21cnjy.com
9. 已知a,b是在同一个平面内的两条直线,根据以下的条件写出a,b的位置关系.
(1)若它们没有交点,则 ;
(2)若它们都平行于直线c,则 ;
(3)若它们有且仅有一个公共点,则 ;
(4)若a∥c,b∥d,且c不平行于d,则 .
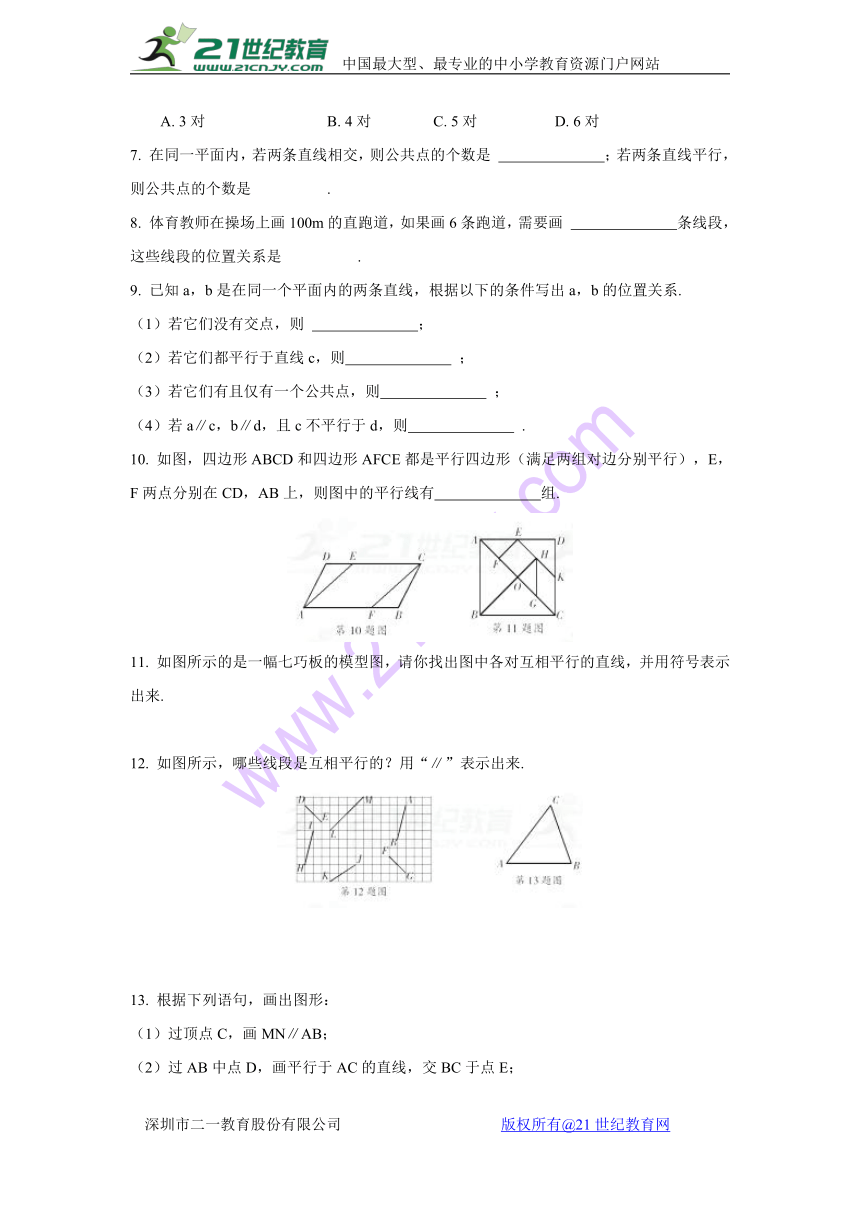
10. 如图,四边形ABCD和四边形AFCE都是平行四边形(满足两组对边分别平行),E,F两点分别在CD,AB上,则图中的平行线有 组.21·cn·jy·com
11. 如图所示的是一幅七巧板的模型图,请你找出图中各对互相平行的直线,并用符号表示出来.
12. 如图所示,哪些线段是互相平行的?用“∥”表示出来.
13. 根据下列语句,画出图形:
(1)过顶点C,画MN∥AB;
(2)过AB中点D,画平行于AC的直线,交BC于点E;
(3)过点B画AC的垂线,交AC于点F.
B组 自主提高
14. 同一平面内的四条直线无论其位置关系如何,它们的交点个数不可能是( )
A. 0个 B. 2个 C. 3个 D. 5个
15. 如图,A,B,C是三棵树,藏宝的地点与这三棵树构成一个平行四边形,作出所有可能是藏宝地点的位置.21世纪教育网版权所有
C组 综合运用
16. 如图,在同一平面内,一组互相平行的直线共有n条(n≥2,且n为正整数),它们和两条平行线a,b相交,构成若干个“#”字形.设构成的“#”字形的个数为x,请找出规律,并填写下表.www.21-cn-jy.com
参考答案
1.1 平行线
【课堂笔记】
1. 同一个平面内
2. 一条
【分层训练】
1—6. ACABAD
7. 1 0
8. 7 平行
9. (1)a∥b (2)a∥b (3)a与b相交 (4)a与b相交
10. 3
11. AD∥BC,AB∥HG∥DC,EF∥BH,EK∥AC.
12. DE∥FG,IH∥AB.
13. 图略
14. B
15. 如图:
∴M1,M2,M3为可能的藏宝地点.
16. 1 3 6 10
1.1 平行线
课堂笔记
1. 在 ,不相交的两条直线叫做平行线.
2. 经过直线外一点,有且只有 直线与这条直线平行.
分层训练
A组 基础训练
1. 在同一平面内,两条不重合的直线的位置关系可能是( )
A. 平行或相交 B. 垂直或相交
C. 垂直或平行 D. 平行、垂直或相交
2. 在同一平面内有三条直线,若其中有且只有两条直线互相平行,则它们交点的个数为( )
A. 0 B. 1 C. 2 D. 3
3. 已知∠AOB与其内部任意一点P,若过点P画一条直线与OA平行,那么这样的直线( )
A. 有且只有一条 B. 有两条 C. 有无数条 D. 不存在
4. 下列说法错误的是( )
A. 在同一平面内,直线a∥b,若c与a相交,则b与c也相交
B. 在同一平面内,直线a与b相交,c与a相交,则b∥c
C. 在同一平面内,两条不平行的直线是相交线
D. 直线AB与CD平行,则AB上所有点都在CD的同侧
5. 如图,将一张长方形纸对折两次,产生的折痕与折痕之间的位置关系是( )
A. 平行 B. 垂直 C. 平行或垂直 D. 无法确定
6. 在如图所示的直三棱柱中,互相平行的棱有( )
A. 3对 B. 4对 C. 5对 D. 6对
7. 在同一平面内,若两条直线相交,则公共点的个数是 ;若两条直线平行,则公共点的个数是 .21教育网
8. 体育教师在操场上画100m的直跑道,如果画6条跑道,需要画 条线段,这些线段的位置关系是 .21cnjy.com
9. 已知a,b是在同一个平面内的两条直线,根据以下的条件写出a,b的位置关系.
(1)若它们没有交点,则 ;
(2)若它们都平行于直线c,则 ;
(3)若它们有且仅有一个公共点,则 ;
(4)若a∥c,b∥d,且c不平行于d,则 .
10. 如图,四边形ABCD和四边形AFCE都是平行四边形(满足两组对边分别平行),E,F两点分别在CD,AB上,则图中的平行线有 组.21·cn·jy·com
11. 如图所示的是一幅七巧板的模型图,请你找出图中各对互相平行的直线,并用符号表示出来.
12. 如图所示,哪些线段是互相平行的?用“∥”表示出来.
13. 根据下列语句,画出图形:
(1)过顶点C,画MN∥AB;
(2)过AB中点D,画平行于AC的直线,交BC于点E;
(3)过点B画AC的垂线,交AC于点F.
B组 自主提高
14. 同一平面内的四条直线无论其位置关系如何,它们的交点个数不可能是( )
A. 0个 B. 2个 C. 3个 D. 5个
15. 如图,A,B,C是三棵树,藏宝的地点与这三棵树构成一个平行四边形,作出所有可能是藏宝地点的位置.21世纪教育网版权所有
C组 综合运用
16. 如图,在同一平面内,一组互相平行的直线共有n条(n≥2,且n为正整数),它们和两条平行线a,b相交,构成若干个“#”字形.设构成的“#”字形的个数为x,请找出规律,并填写下表.www.21-cn-jy.com
参考答案
1.1 平行线
【课堂笔记】
1. 同一个平面内
2. 一条
【分层训练】
1—6. ACABAD
7. 1 0
8. 7 平行
9. (1)a∥b (2)a∥b (3)a与b相交 (4)a与b相交
10. 3
11. AD∥BC,AB∥HG∥DC,EF∥BH,EK∥AC.
12. DE∥FG,IH∥AB.
13. 图略
14. B
15. 如图:
∴M1,M2,M3为可能的藏宝地点.
16. 1 3 6 10
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
