浙教版数学七年级下册期末复习一 平行线 教案(含答案)
文档属性
| 名称 | 浙教版数学七年级下册期末复习一 平行线 教案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 212.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-06 15:12:37 | ||
图片预览


文档简介
期末复习一 平行线
复习目标
要求
知识与方法
了解
同位角、内错角、同旁内角的概念
平行线的概念及表示
图形平移的意义及性质
理解
在图形中辨认同位角、内错角及同旁内角
平行线的基本事实,过直线外一点作已知直线的平行线
平行线的判定及性质
作一个图形平移后所得的图形
运用
平行线判定及性质的综合运用
图形平移在自然界和现实生活中的应用
必备知识与防范点
一、必备知识:
1. 在同一平面内, 的两条直线叫做平行线. 经过直线外一点, 一条直线平行于已知直线.21·cn·jy·com
2. 平行线的判定:
,两直线平行; ,两直线平行; 互补, .
3. 平行线的性质:
两直线平行, 相等;两直线平行,内错角相等;两直线平行,同旁内角 .
4. 平移不改变图形的 和 . 一个图形和它经过平移所得的图形中,两组对应点的连线 (或在同一直线上)且 .www.21-cn-jy.com
二、防范点:
1. 平行线概念注意不要遗漏在同一平面内的前提.
2. 平行线判定及性质注意同旁内角是互补关系,不是相等.
例题精析
考点一 平行线的概念
例1 下列说法正确的个数有( )
①不相交的两条直线是平行线;②在同一平面内,两条直线的位置关系有两种;③若线段AB与CD没有交点,则AB∥CD;④若a∥b,b∥c,则a与c不相交.
A. 1个 B. 2个 C. 3个 D. 4个
反思:平行线概念有个在同一平面内的前提,注意不要遗漏;不相交的线段也不一定平行.
考点二 三线八角
例2 (1)如图,∠1与∠2是( )
A. 对顶角 B. 同位角 C. 内错角 D. 同旁内角
(2)如图,用数字标出的八个角中,同位角、内错角、同旁内角分别有哪些?请把它们一一写出来.
反思:判断三线八角关键看两个角的边所成的图形,“F”形为同位角,“Z”形为内错角,“U”形为同旁内角.21·世纪*教育网
考点三 平行线的判定及性质
例3 如图,已知∠1=∠2=120°,∠3=100°.
(1)直线l1与直线l2平行吗?为什么?
(2)求∠4的度数.
反思:判定平行往往是找寻一组同位角相等、内错角相等或同旁内角互补,而求角度常要用到平行线的性质.
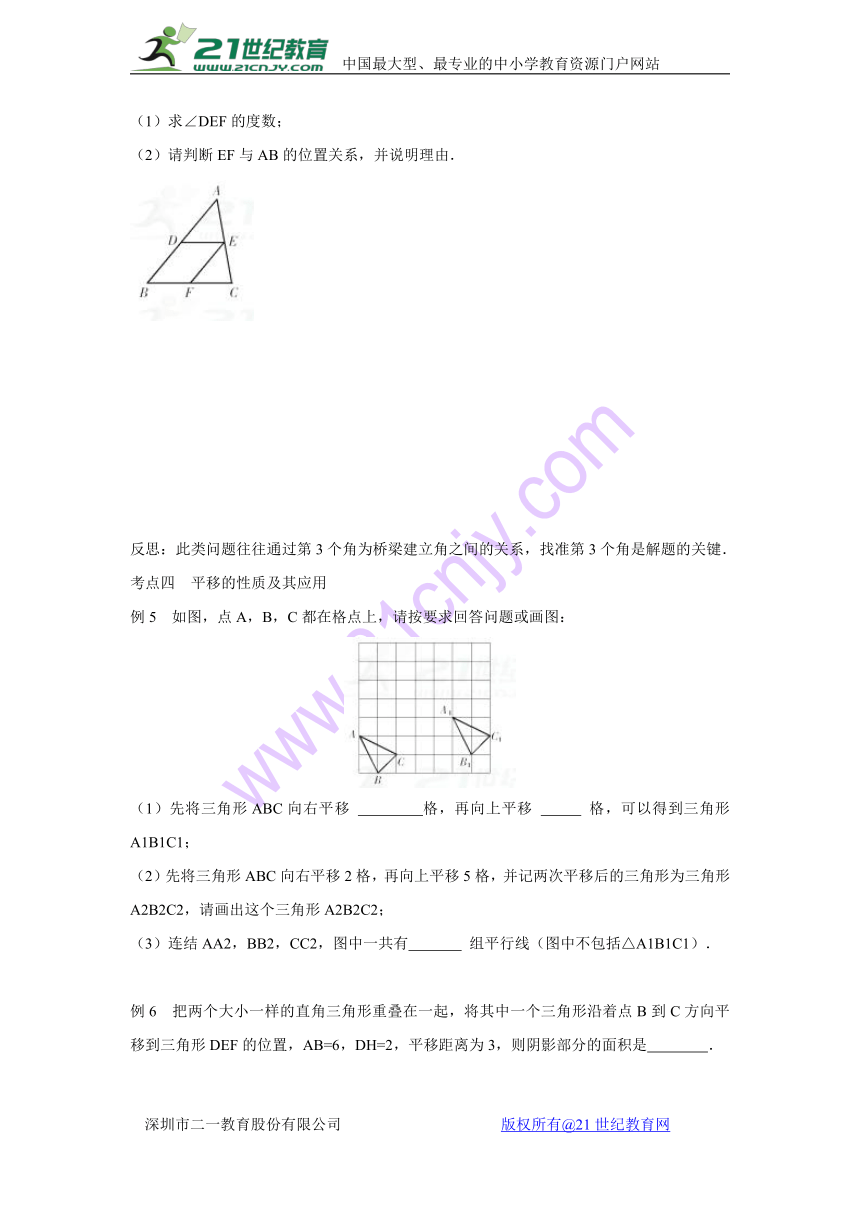
例4 如图,已知DE∥BC,EF平分∠DEC,且∠ABC=55°,∠C=70°.
(1)求∠DEF的度数;
(2)请判断EF与AB的位置关系,并说明理由.
反思:此类问题往往通过第3个角为桥梁建立角之间的关系,找准第3个角是解题的关键.
考点四 平移的性质及其应用
例5 如图,点A,B,C都在格点上,请按要求回答问题或画图:
(1)先将三角形ABC向右平移 格,再向上平移 格,可以得到三角形A1B1C1;【来源:21·世纪·教育·网】
(2)先将三角形ABC向右平移2格,再向上平移5格,并记两次平移后的三角形为三角形A2B2C2,请画出这个三角形A2B2C2;www-2-1-cnjy-com
(3)连结AA2,BB2,CC2,图中一共有 组平行线(图中不包括△A1B1C1).
例6 把两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B到C方向平移到三角形DEF的位置,AB=6,DH=2,平移距离为3,则阴影部分的面积是 .
反思:用平移解决实际问题,往往是运用平移的性质求出角的度数或线段的长度,在解决过程中要合理运用转化思想.2-1-c-n-j-y
校内练习
1.如图,已知直线l1∥l2,将一把含30°角的直角三角尺按如图所示的位置放置,∠1=25°,则∠2等于( )2·1·c·n·j·y
A. 30° B. 35° C. 40° D. 45°
2. 如图所示,把一张长方形纸片ABCD沿EF折叠,若∠EFG=50°,则∠DEG的度数为 .21教育网
3. 某地下车库出口处“两段式栏杆”如图1所示,点A是栏杆转动的交点,点E是栏杆两段的连接点. 当车辆经过时,栏杆升起的两个位置如图2所示,其中EF始终与BC平行,则∠1,∠2,∠3三者之间的关系是 .21*cnjy*com
4. 如图,已知∠B=∠C.
(1)若AD∥BC,则AD平分∠EAC吗?请说明理由;
(2)若∠EAC+∠BAC=180°,
AD平分∠EAC,则AD∥BC吗?请说明理由.
5. 已知,如图,EF∥AD,∠1=∠2.
(1)求证:DG∥AB;
(2)若∠CGD=80°,∠1=40°,求∠CAD的大小.
参考答案
期末复习一 平行线
【必备知识与防范点】
1. 不相交 有且只有
2. 同位角相等 内错角相等 同旁内角 两直线平行
3. 同位角 互补
4. 形状 大小 平行 相等
【例题精析】
例1 B
例2 (1)B (2)同位角∠2与∠8,∠3与∠7,∠4与∠6;内错角:∠1与∠4,∠3与∠5,∠2与∠6,∠4与∠8;同旁内角:∠3与∠6,∠2与∠5,∠2与∠4,∠4与∠5.
例3 (1)平行,理由如下:
设∠2的对顶角是∠5,∵∠5=∠2=∠1=120°,∴l1∥l2.
(2)∵l1∥l2,∴∠4=∠3=100°.
例4 (1)∵DE∥BC,∠C=70°,∴∠DEC=180°-∠C=110°,∵EF平分∠DEC,∴∠DEF=∠CEF=∠DEC=55°.21世纪教育网版权所有
(2)EF与AB平行,理由如下:
由(1)得∠DEF=55°,又∵DE∥BC,∴∠EFC
=∠DEF=55°,∵∠ABC=55°,∴∠EFC=∠ABC,∴EF∥AB.
例5 (1)5 1 (2)画图略 (3)6
例6 15
【校内练习】
1. B
2. 100°
3. ∠2=∠1+∠3
4. (1)∵AD∥BC,∴∠B=∠EAD,∠C=∠DAC,∵∠B=∠C,∴∠EAD=∠DAC,∴AD平分∠EAC.21cnjy.com
(2)∵AD平分∠EAC,∴∠EAD=∠DAC,又∵∠EAC+∠BAC=180°,∴2∠DAC+∠BAC=180°,又∵∠B=∠C,∴2∠C+∠BAC=180°,∴∠DAC=∠C,∴AD∥BC.
5. (1)∵EF∥AD,∴∠2=∠3,∵∠1=∠2,∴∠3=∠1,∴DG∥AB.
(2)∠CAD=40°
复习目标
要求
知识与方法
了解
同位角、内错角、同旁内角的概念
平行线的概念及表示
图形平移的意义及性质
理解
在图形中辨认同位角、内错角及同旁内角
平行线的基本事实,过直线外一点作已知直线的平行线
平行线的判定及性质
作一个图形平移后所得的图形
运用
平行线判定及性质的综合运用
图形平移在自然界和现实生活中的应用
必备知识与防范点
一、必备知识:
1. 在同一平面内, 的两条直线叫做平行线. 经过直线外一点, 一条直线平行于已知直线.21·cn·jy·com
2. 平行线的判定:
,两直线平行; ,两直线平行; 互补, .
3. 平行线的性质:
两直线平行, 相等;两直线平行,内错角相等;两直线平行,同旁内角 .
4. 平移不改变图形的 和 . 一个图形和它经过平移所得的图形中,两组对应点的连线 (或在同一直线上)且 .www.21-cn-jy.com
二、防范点:
1. 平行线概念注意不要遗漏在同一平面内的前提.
2. 平行线判定及性质注意同旁内角是互补关系,不是相等.
例题精析
考点一 平行线的概念
例1 下列说法正确的个数有( )
①不相交的两条直线是平行线;②在同一平面内,两条直线的位置关系有两种;③若线段AB与CD没有交点,则AB∥CD;④若a∥b,b∥c,则a与c不相交.
A. 1个 B. 2个 C. 3个 D. 4个
反思:平行线概念有个在同一平面内的前提,注意不要遗漏;不相交的线段也不一定平行.
考点二 三线八角
例2 (1)如图,∠1与∠2是( )
A. 对顶角 B. 同位角 C. 内错角 D. 同旁内角
(2)如图,用数字标出的八个角中,同位角、内错角、同旁内角分别有哪些?请把它们一一写出来.
反思:判断三线八角关键看两个角的边所成的图形,“F”形为同位角,“Z”形为内错角,“U”形为同旁内角.21·世纪*教育网
考点三 平行线的判定及性质
例3 如图,已知∠1=∠2=120°,∠3=100°.
(1)直线l1与直线l2平行吗?为什么?
(2)求∠4的度数.
反思:判定平行往往是找寻一组同位角相等、内错角相等或同旁内角互补,而求角度常要用到平行线的性质.
例4 如图,已知DE∥BC,EF平分∠DEC,且∠ABC=55°,∠C=70°.
(1)求∠DEF的度数;
(2)请判断EF与AB的位置关系,并说明理由.
反思:此类问题往往通过第3个角为桥梁建立角之间的关系,找准第3个角是解题的关键.
考点四 平移的性质及其应用
例5 如图,点A,B,C都在格点上,请按要求回答问题或画图:
(1)先将三角形ABC向右平移 格,再向上平移 格,可以得到三角形A1B1C1;【来源:21·世纪·教育·网】
(2)先将三角形ABC向右平移2格,再向上平移5格,并记两次平移后的三角形为三角形A2B2C2,请画出这个三角形A2B2C2;www-2-1-cnjy-com
(3)连结AA2,BB2,CC2,图中一共有 组平行线(图中不包括△A1B1C1).
例6 把两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B到C方向平移到三角形DEF的位置,AB=6,DH=2,平移距离为3,则阴影部分的面积是 .
反思:用平移解决实际问题,往往是运用平移的性质求出角的度数或线段的长度,在解决过程中要合理运用转化思想.2-1-c-n-j-y
校内练习
1.如图,已知直线l1∥l2,将一把含30°角的直角三角尺按如图所示的位置放置,∠1=25°,则∠2等于( )2·1·c·n·j·y
A. 30° B. 35° C. 40° D. 45°
2. 如图所示,把一张长方形纸片ABCD沿EF折叠,若∠EFG=50°,则∠DEG的度数为 .21教育网
3. 某地下车库出口处“两段式栏杆”如图1所示,点A是栏杆转动的交点,点E是栏杆两段的连接点. 当车辆经过时,栏杆升起的两个位置如图2所示,其中EF始终与BC平行,则∠1,∠2,∠3三者之间的关系是 .21*cnjy*com
4. 如图,已知∠B=∠C.
(1)若AD∥BC,则AD平分∠EAC吗?请说明理由;
(2)若∠EAC+∠BAC=180°,
AD平分∠EAC,则AD∥BC吗?请说明理由.
5. 已知,如图,EF∥AD,∠1=∠2.
(1)求证:DG∥AB;
(2)若∠CGD=80°,∠1=40°,求∠CAD的大小.
参考答案
期末复习一 平行线
【必备知识与防范点】
1. 不相交 有且只有
2. 同位角相等 内错角相等 同旁内角 两直线平行
3. 同位角 互补
4. 形状 大小 平行 相等
【例题精析】
例1 B
例2 (1)B (2)同位角∠2与∠8,∠3与∠7,∠4与∠6;内错角:∠1与∠4,∠3与∠5,∠2与∠6,∠4与∠8;同旁内角:∠3与∠6,∠2与∠5,∠2与∠4,∠4与∠5.
例3 (1)平行,理由如下:
设∠2的对顶角是∠5,∵∠5=∠2=∠1=120°,∴l1∥l2.
(2)∵l1∥l2,∴∠4=∠3=100°.
例4 (1)∵DE∥BC,∠C=70°,∴∠DEC=180°-∠C=110°,∵EF平分∠DEC,∴∠DEF=∠CEF=∠DEC=55°.21世纪教育网版权所有
(2)EF与AB平行,理由如下:
由(1)得∠DEF=55°,又∵DE∥BC,∴∠EFC
=∠DEF=55°,∵∠ABC=55°,∴∠EFC=∠ABC,∴EF∥AB.
例5 (1)5 1 (2)画图略 (3)6
例6 15
【校内练习】
1. B
2. 100°
3. ∠2=∠1+∠3
4. (1)∵AD∥BC,∴∠B=∠EAD,∠C=∠DAC,∵∠B=∠C,∴∠EAD=∠DAC,∴AD平分∠EAC.21cnjy.com
(2)∵AD平分∠EAC,∴∠EAD=∠DAC,又∵∠EAC+∠BAC=180°,∴2∠DAC+∠BAC=180°,又∵∠B=∠C,∴2∠C+∠BAC=180°,∴∠DAC=∠C,∴AD∥BC.
5. (1)∵EF∥AD,∴∠2=∠3,∵∠1=∠2,∴∠3=∠1,∴DG∥AB.
(2)∠CAD=40°
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
