浙教版数学七年级下册期末复习教案五 分式
文档属性
| 名称 | 浙教版数学七年级下册期末复习教案五 分式 |  | |
| 格式 | zip | ||
| 文件大小 | 161.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-06 15:11:32 | ||
图片预览



文档简介
期末复习五 分式
复习目标
要求
知识与方法
了解
分式的概念
分式方程的概念
分式方程根的检验
理解
分式的基本性质及分式符号法则
分式的约分、通分
分式的加、减、乘、除运算
解可化为一元一次方程的分式方程
运用
利用分式及其运算解决简单的实际问题
列分式方程解简单的应用题
必备知识与防范点
一、必备知识:
1. 表示两个整式相除,且除式中含有 ,这样的代数式叫做分式.
2. 分式的分子与分母都乘以(或除以) 的整式,分式的值不变.
3. 分式乘分式,用分子的积做积的 , 做积的分母;分式除以分式,把 颠倒位置后,与被除式相乘.21·世纪*教育网
4. 同分母的分式相加减,把 相加减, 不变. 把分母不相同的几个分式,化成分母相同的分式,叫做 . 一般地,异分母分式相加减的方法是:先 ,化为同分母的分式,再按同分母分式相加减法则进行计算.【来源:21cnj*y.co*m】
5. 只含分式,或分式和整式,并且分母中含有 的方程叫做分式方程.解分式方程必须 . 把求得的根代入 ,或代入原方程两边所乘的 ,使分母为零的根是 ,增根必须舍去.【出处:21教育名师】
二、防范点:
1. 分式基本性质使用过程中始终要注意乘以(或除以)的整式不能为零.
2. 分式乘除运算要注意运算顺序,约分过程中要先把分子、分母中的多项式因式分解,才能进行约分.
3. 分式的加减运算是通分,而解分式方程往往是去分母,两者不要混淆.
4. 分式方程一定不要遗漏验根.
例题精析
考点一 分式、分式方程概念
例1 (1)在,,,中,属于分式的个数为( )
A. 0个 B. 1个 C. 2个 D. 3个
(2)在①=5;②(x-1)+(x+1)=4;③-=1;④+=-1;⑤(3x-7)中,分式方程有( )【版权所有:21教育】
A. 1个 B. 2个 C. 3个 D. 4个
(3)当x= 时,分式无意义.
(4)分式的值为0,则b= .
反思:判断分式及分式方程,主要看分母中是否含有字母,方程还应是一个等式. 分式无意义则分母等于零;分式的值为零则分子等于零且分母不等于零,不要遗漏分母不为零.
考点二 分式的基本性质及符号法则
例2 (1)不改变分式的值,把分子和分母中各项的系数都化为整数,则所得的结果为( )
A. B. C. D.
(2)下列各式中,变形不正确的是( )
A. =- B. =
C. =- D. -=
(3)若把分式中的x和y都扩大为原来的3倍,那么分式的值( )
A. 扩大为原来的3倍
B. 不变
C. 缩小为原来的
D. 缩小为原来的
反思:分式的基本性质及符号法则是分式运算中两个重要的法则,分式基本性质运用过程中要注意乘或除以的式子不能为零,符号法则运用过程中要注意变两个位置的符号,不要产生错误.www-2-1-cnjy-com
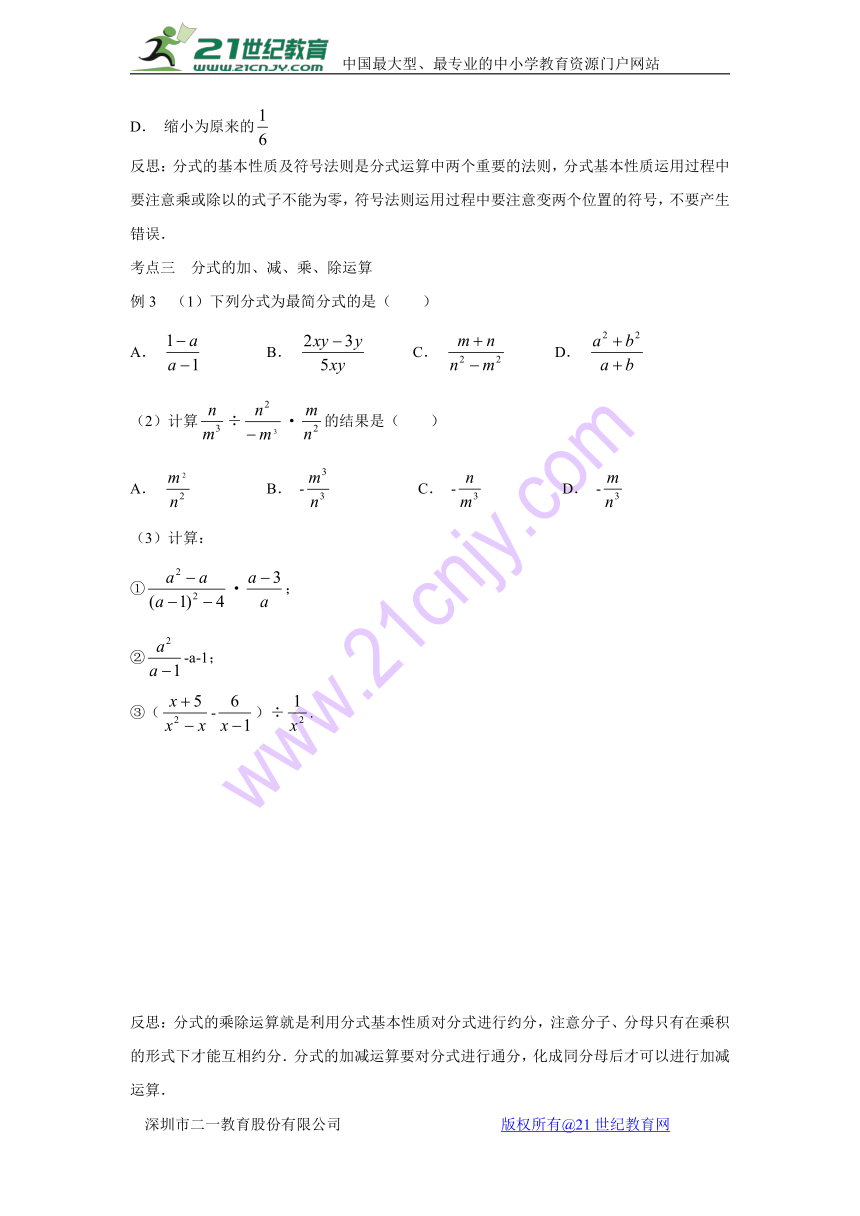
考点三 分式的加、减、乘、除运算
例3 (1)下列分式为最简分式的是( )
A. B. C. D.
(2)计算÷·的结果是( )
A. B. - C. - D. -
(3)计算:
①·;
②-a-1;
③(-)÷.
反思:分式的乘除运算就是利用分式基本性质对分式进行约分,注意分子、分母只有在乘积的形式下才能互相约分.分式的加减运算要对分式进行通分,化成同分母后才可以进行加减运算.21教育名师原创作品
考点四 分式相关的条件求值
例4 (1)已知b=3a,a=5c,求的值.
(2)已知-=4,求的值.
(3)已知==,求的值.
反思:条件求值就是把条件进行转化,找出不同字母之间的关系,把字母与字母的关系代入原分式即可解决问题.在运算过程中常用到整体思想,有时也可以通过换元来简化运算.
考点五 分式方程及分式方程的应用
例5 (1)解分式方程-=-1,去分母后,得( )
A. 3(x-5)-(x+5)(x-3)=-1
B. 3x-5-(x+5)(x-3)=-(x+5)(x-5)
C. 3x-15-x2+15=-(x+5)(x-5)
D. 3(x-5)-(x+5)(x-3)=-(x+5)(x-5)
(2)已知关于x的方程2+=有增根,则a的值为( )
A. 1 B. -1 C. 0 D. 2
(3)七年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达. 已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度.设学生骑车的速度为x千米/小时,则所列方程正确的是( )
A. =- B. =-20
C. =+ D. =+20
(4)解下列分式方程:
①+=;
②+=1.
(5)某工程队(有甲、乙两组)承包一项工程,规定若干天内完成.
①已知甲组单独完成这项工程所需时间比规定时间多30天,乙组单独完成这项工程所需时间比规定时间多12天,如果甲乙两组先合做20天,剩下的由甲组单独做,恰好按规定的时间完成,那么规定的时间是多少天?21世纪教育网版权所有
②实际工作中,甲乙两组合做完成这项工程的后,工程队又承包了新工程,需要抽调一组过去,从按时完成任务考虑,你认为留下哪一组更好?说明理由.
反思:解分式方程要先去分母,去分母时注意不要漏乘,最后还必须得验根. 分式方程的增根问题,一般过程是先去分母,再找增根,代入增根后求解未知数即可,但如果是无解问题要考虑多种情况.21·cn·jy·com
校内练习
1. 如果分式的值是整数,则整数x可取的值的个数是( )
A. 10个 B. 8个 C. 6个 D. 4个
2. 若x=4是方程=8的解,则a= .
3. 约分化简:= ;= .
4. 已知关于x的方程+=无解,则a的值为 .
5. 某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元. 已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少100元.www.21-cn-jy.com
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?请说明理由.
6. 甲,乙两人两次同时在同一家超市购买糖果,两次购买糖果的价格分别为每千克a元和b元(a≠b). 甲每次购买10千克糖果,乙每次花10元钱购买糖果.21cnjy.com
(1)甲两次购买糖果共付款 元,乙两次共购买 千克糖果(用含a,b的代数式表示);2·1·c·n·j·y
(2)请你判断甲,乙两人的购买方式哪一种购买的平均价格更低?请说明理由.
参考答案
期末复习五 分式
【必备知识与防范点】
1. 字母
2. 同一个不等于零
3. 分子 分母的积 除式的分子和分母
4. 分子 分母 通分 通分
5. 字母 验根 原方程 公分母 增根
【例题精析】
例1 (1)C (2)B (3)3 (4)-2
例2 (1)B (2)D (3)C
例3 (1)D (2)D
(3)①·=·=
②-a-1=-=
③(-)÷=[-]·x2=·x2=-5x
例4 (1)由条件得,a=5c,b=15c,代入分式得,原式===-16
(2)由-=4,得b-a=4ab,即a-b=-4ab,∴原式====6
(3)设===k,则x=2k,y=3k,z=4k,代入原分式得,∴原式===.
例5 (1)D (2)A (3)C
(4)①计算得x=1,是增根,所以原方程无解 ②x=0
(5)①设规定的时间是x天,则甲单独完成需要(x+30)天,乙单独完成需要(x+12)天,由题意,得20(+)+×(x-20)=1,解得:x=24. 经检验,x=24是原方程的根,答:规定的时间是24天.21教育网
②∵规定时间是24天,∴甲单独完成需要24+30=54天,乙单独完成需要24+12=36天. 留下甲完成需要的时间是:÷(+)+(1-)÷=18+9=27天>24天,不能在规定时间完成任务;留下乙完成需要的时间是:÷(+)+(1-)÷=18+6=24天,能在规定时间完成任务. ∴留下乙组较好.【来源:21·世纪·教育·网】
【校内练习】
1. B
2. 2
3.
4. -4或6或1
5. (1)设甲车单独运完此堆垃圾需运x趟,则乙车单独运完此堆垃圾需运2x趟. 根据题意得12(+)=1. 解得x=18,则2x=36. 经检验,x=18是原方程的解.
答:甲车单独运完需18趟,乙车单独运完需36趟.
(2)设甲车每一趟的运费是a元,由题意得
12a+12(a-100)=4800,解得a=250,则乙车每一趟的费用是250-100=150(元),单独租用甲车总费用是18×250=4500(元),单独租用乙车总费用是36×150=5400(元),4500<5400,故单独租用一台车,租用甲车合算.2-1-c-n-j-y
6. (1)(10a+10b) (+)
(2)甲两次购买糖果的平均价格:元;乙两次购买糖果的平均价格:=元. 则-=>0,则乙的平均价格更低.21*cnjy*com
复习目标
要求
知识与方法
了解
分式的概念
分式方程的概念
分式方程根的检验
理解
分式的基本性质及分式符号法则
分式的约分、通分
分式的加、减、乘、除运算
解可化为一元一次方程的分式方程
运用
利用分式及其运算解决简单的实际问题
列分式方程解简单的应用题
必备知识与防范点
一、必备知识:
1. 表示两个整式相除,且除式中含有 ,这样的代数式叫做分式.
2. 分式的分子与分母都乘以(或除以) 的整式,分式的值不变.
3. 分式乘分式,用分子的积做积的 , 做积的分母;分式除以分式,把 颠倒位置后,与被除式相乘.21·世纪*教育网
4. 同分母的分式相加减,把 相加减, 不变. 把分母不相同的几个分式,化成分母相同的分式,叫做 . 一般地,异分母分式相加减的方法是:先 ,化为同分母的分式,再按同分母分式相加减法则进行计算.【来源:21cnj*y.co*m】
5. 只含分式,或分式和整式,并且分母中含有 的方程叫做分式方程.解分式方程必须 . 把求得的根代入 ,或代入原方程两边所乘的 ,使分母为零的根是 ,增根必须舍去.【出处:21教育名师】
二、防范点:
1. 分式基本性质使用过程中始终要注意乘以(或除以)的整式不能为零.
2. 分式乘除运算要注意运算顺序,约分过程中要先把分子、分母中的多项式因式分解,才能进行约分.
3. 分式的加减运算是通分,而解分式方程往往是去分母,两者不要混淆.
4. 分式方程一定不要遗漏验根.
例题精析
考点一 分式、分式方程概念
例1 (1)在,,,中,属于分式的个数为( )
A. 0个 B. 1个 C. 2个 D. 3个
(2)在①=5;②(x-1)+(x+1)=4;③-=1;④+=-1;⑤(3x-7)中,分式方程有( )【版权所有:21教育】
A. 1个 B. 2个 C. 3个 D. 4个
(3)当x= 时,分式无意义.
(4)分式的值为0,则b= .
反思:判断分式及分式方程,主要看分母中是否含有字母,方程还应是一个等式. 分式无意义则分母等于零;分式的值为零则分子等于零且分母不等于零,不要遗漏分母不为零.
考点二 分式的基本性质及符号法则
例2 (1)不改变分式的值,把分子和分母中各项的系数都化为整数,则所得的结果为( )
A. B. C. D.
(2)下列各式中,变形不正确的是( )
A. =- B. =
C. =- D. -=
(3)若把分式中的x和y都扩大为原来的3倍,那么分式的值( )
A. 扩大为原来的3倍
B. 不变
C. 缩小为原来的
D. 缩小为原来的
反思:分式的基本性质及符号法则是分式运算中两个重要的法则,分式基本性质运用过程中要注意乘或除以的式子不能为零,符号法则运用过程中要注意变两个位置的符号,不要产生错误.www-2-1-cnjy-com
考点三 分式的加、减、乘、除运算
例3 (1)下列分式为最简分式的是( )
A. B. C. D.
(2)计算÷·的结果是( )
A. B. - C. - D. -
(3)计算:
①·;
②-a-1;
③(-)÷.
反思:分式的乘除运算就是利用分式基本性质对分式进行约分,注意分子、分母只有在乘积的形式下才能互相约分.分式的加减运算要对分式进行通分,化成同分母后才可以进行加减运算.21教育名师原创作品
考点四 分式相关的条件求值
例4 (1)已知b=3a,a=5c,求的值.
(2)已知-=4,求的值.
(3)已知==,求的值.
反思:条件求值就是把条件进行转化,找出不同字母之间的关系,把字母与字母的关系代入原分式即可解决问题.在运算过程中常用到整体思想,有时也可以通过换元来简化运算.
考点五 分式方程及分式方程的应用
例5 (1)解分式方程-=-1,去分母后,得( )
A. 3(x-5)-(x+5)(x-3)=-1
B. 3x-5-(x+5)(x-3)=-(x+5)(x-5)
C. 3x-15-x2+15=-(x+5)(x-5)
D. 3(x-5)-(x+5)(x-3)=-(x+5)(x-5)
(2)已知关于x的方程2+=有增根,则a的值为( )
A. 1 B. -1 C. 0 D. 2
(3)七年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达. 已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度.设学生骑车的速度为x千米/小时,则所列方程正确的是( )
A. =- B. =-20
C. =+ D. =+20
(4)解下列分式方程:
①+=;
②+=1.
(5)某工程队(有甲、乙两组)承包一项工程,规定若干天内完成.
①已知甲组单独完成这项工程所需时间比规定时间多30天,乙组单独完成这项工程所需时间比规定时间多12天,如果甲乙两组先合做20天,剩下的由甲组单独做,恰好按规定的时间完成,那么规定的时间是多少天?21世纪教育网版权所有
②实际工作中,甲乙两组合做完成这项工程的后,工程队又承包了新工程,需要抽调一组过去,从按时完成任务考虑,你认为留下哪一组更好?说明理由.
反思:解分式方程要先去分母,去分母时注意不要漏乘,最后还必须得验根. 分式方程的增根问题,一般过程是先去分母,再找增根,代入增根后求解未知数即可,但如果是无解问题要考虑多种情况.21·cn·jy·com
校内练习
1. 如果分式的值是整数,则整数x可取的值的个数是( )
A. 10个 B. 8个 C. 6个 D. 4个
2. 若x=4是方程=8的解,则a= .
3. 约分化简:= ;= .
4. 已知关于x的方程+=无解,则a的值为 .
5. 某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元. 已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少100元.www.21-cn-jy.com
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?请说明理由.
6. 甲,乙两人两次同时在同一家超市购买糖果,两次购买糖果的价格分别为每千克a元和b元(a≠b). 甲每次购买10千克糖果,乙每次花10元钱购买糖果.21cnjy.com
(1)甲两次购买糖果共付款 元,乙两次共购买 千克糖果(用含a,b的代数式表示);2·1·c·n·j·y
(2)请你判断甲,乙两人的购买方式哪一种购买的平均价格更低?请说明理由.
参考答案
期末复习五 分式
【必备知识与防范点】
1. 字母
2. 同一个不等于零
3. 分子 分母的积 除式的分子和分母
4. 分子 分母 通分 通分
5. 字母 验根 原方程 公分母 增根
【例题精析】
例1 (1)C (2)B (3)3 (4)-2
例2 (1)B (2)D (3)C
例3 (1)D (2)D
(3)①·=·=
②-a-1=-=
③(-)÷=[-]·x2=·x2=-5x
例4 (1)由条件得,a=5c,b=15c,代入分式得,原式===-16
(2)由-=4,得b-a=4ab,即a-b=-4ab,∴原式====6
(3)设===k,则x=2k,y=3k,z=4k,代入原分式得,∴原式===.
例5 (1)D (2)A (3)C
(4)①计算得x=1,是增根,所以原方程无解 ②x=0
(5)①设规定的时间是x天,则甲单独完成需要(x+30)天,乙单独完成需要(x+12)天,由题意,得20(+)+×(x-20)=1,解得:x=24. 经检验,x=24是原方程的根,答:规定的时间是24天.21教育网
②∵规定时间是24天,∴甲单独完成需要24+30=54天,乙单独完成需要24+12=36天. 留下甲完成需要的时间是:÷(+)+(1-)÷=18+9=27天>24天,不能在规定时间完成任务;留下乙完成需要的时间是:÷(+)+(1-)÷=18+6=24天,能在规定时间完成任务. ∴留下乙组较好.【来源:21·世纪·教育·网】
【校内练习】
1. B
2. 2
3.
4. -4或6或1
5. (1)设甲车单独运完此堆垃圾需运x趟,则乙车单独运完此堆垃圾需运2x趟. 根据题意得12(+)=1. 解得x=18,则2x=36. 经检验,x=18是原方程的解.
答:甲车单独运完需18趟,乙车单独运完需36趟.
(2)设甲车每一趟的运费是a元,由题意得
12a+12(a-100)=4800,解得a=250,则乙车每一趟的费用是250-100=150(元),单独租用甲车总费用是18×250=4500(元),单独租用乙车总费用是36×150=5400(元),4500<5400,故单独租用一台车,租用甲车合算.2-1-c-n-j-y
6. (1)(10a+10b) (+)
(2)甲两次购买糖果的平均价格:元;乙两次购买糖果的平均价格:=元. 则-=>0,则乙的平均价格更低.21*cnjy*com
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
