6.3 扇形统计图同步练习

21世纪教育网 –中小学教育资源及组卷应用平台
6.3 扇形统计图同步练习
　班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.扇形统计图是用整个圆表示总数用圆内各个扇形的大小表示各部分数量占总数的百分数．通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系．用整个圆的面积表示总数（单位1），用圆的扇形面积表示各部分占总数的百分数．
2.扇形图的特点：从扇形图上可以清楚地看出各部分数量和总数量之间的关系．
3.制作扇形图的步骤
①根据有关数据先算出各部分在总体中所占的百分数，再算出各部分圆心角的度数，公式是各部分扇形圆心角的度数=部分占总体的百分比×360°．
②按比例取适当半径画一个圆；按扇形圆心角的度数用量角器在圆内量出各个扇形的圆心角的度数；
④在各扇形内写上相应的名称及百分数，并用不同的标记把各扇形区分开来．
基础知识和能力拓展精练
一、选择题
1．根据呼和浩特市第一季度用电量的扇形统计图，则2月份用电量占第一季度用电量的百分比为（ 　　）
A. 60% B. 64% C. 54% D. 74%
2．要反映2015年末嘉兴市各个县（区）常住人口占嘉兴市总人口的比例，宜采用（ ）
A. 条形统计图 B. 折线统计图 C. 扇形统计图 D. 频数直方图
3．如图，某实验中学制作了学生选择象棋、曲艺、园艺、制陶四门业余课程情况的扇形统计图，从中可以看出选择制陶的学生占(　　)
A. 25% B. 30% C. 35% D. 40%
4．如图是P，Q两国2016年财政经费支出情况的扇形统计图．根据统计图，下面对两国全年教育经费支出判断正确的是(　 　)
A. P国比Q国多 B. Q国比P国多 C. P国与Q国一样多 D. 无法确定哪国多
5．“救死扶伤”是我国的传统美德，某媒体就“老人摔倒该不该扶”进行了调查，将得到的数据经统计分析后绘制成如图所示的扇形统计图，根据统计图判断下列说法，其中错误的一项是(　 　)
A. 认为依情况而定的占 B. 认为该扶的在统计图中所对应的圆心角是
C. 认为不该扶的占 D. 认为该扶的占
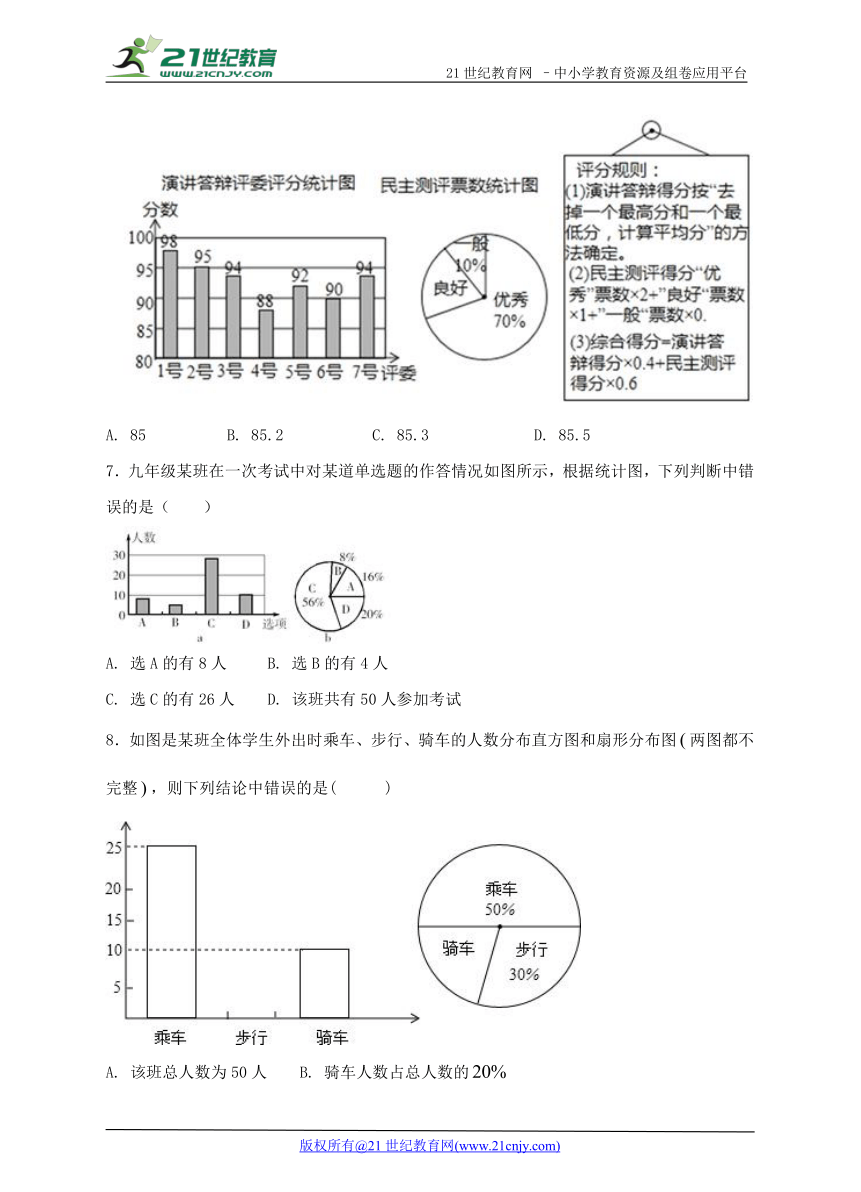
6．小明参加班长竞选，需进行演讲答辩与民主测评，民主测评时一人一票，按“优秀、良好、一般”三选一投票．如图是7位评委对小明“演讲答辩”的评分统计图及全班50位同学民主测评票数统计图．根据统计图表中的数据和评分规则，本次竞选中小明的综合得分数为（　　）
A. 85 B. 85.2 C. 85.3 D. 85.5
7．九年级某班在一次考试中对某道单选题的作答情况如图所示，根据统计图，下列判断中错误的是（ ）
A. 选A的有8人 B. 选B的有4人
C. 选C的有26人 D. 该班共有50人参加考试
8．如图是某班全体学生外出时乘车、步行、骑车的人数分布直方图和扇形分布图两图都不完整，则下列结论中错误的是(　 　)
A. 该班总人数为50人 B. 骑车人数占总人数的
C. 步行人数为30人 D. 乘车人数是骑车人数的倍
二、填空题
9．扇形统计图中，A,B,C,D 4个扇形所表示的数据个数的比是，则扇形C的圆心角的度数为
10．2018年春节期间，反季游成为出境游的热门，中国游客青睐的目的地仍主要集中在温暖的东南亚地区．据调查发现2018年春节期间出境游约有700万人，游客目的地分布情况的扇形图如图所示，从中可知出境游东南亚地区的游客约有________万人．
11．如图，这是小新在询问了父母后绘制的去年全家的开支情况扇形统计图，如果他家去年总开支为6万元，那么用于教育的支出为_____万元．
12．某校组织了主题为“共建生态岛”的电子小报作品征集活动，先从中随机抽取了部分作品，按四个等级进行评分，然后根据统计结果绘制了如下两幅不完整的统计图，那么此次抽取的作品中等级为B的作品数为_________．
13．记录某足球队全年比赛结果（“胜”、“负”、“平”）的条形统计图和扇形统计图（不完整）如下：
根据图中信息，该足球队全年比赛胜了_____场．
14．如图，为某冷饮店一天售出各种口味雪糕数量的扇形统计图，其中售出红豆口味的雪糕200支，那么售出奶油口味雪糕的数量是_____支．
15．如图是某农场里三种蔬菜种植面积的扇形统计图，若西红柿种植面积为4.2公顷，则这三种蔬菜种植总面积是________公顷，表示黄瓜的扇形圆心角的度数为________．
三、解答题
16．“精准扶贫”这是新时期党和国家扶贫工作的精髓和亮点．某校团委随机抽取部分学生，对他们是否了解关于“精准扶贫”的情况进行调查，调查结果有三种：A、了解很多；B、了解一点；C、不了解．团委根据调查的数据进行整理，绘制了尚不完整的统计图如下，图1中C区域的圆心角为36°，请根据统计图中的相关的信息，解答下列问题：
（1）求本次活动共调查了　 　名学生；图1中，B区域的圆心角度是　 　；在抽取的学生中调查结果的中位数落在　 　区域里．
（2）补全条形统计图．
（3）若该校有1200名学生，请估算该校不是了解很多的学生人数．
17．某地区教育部门为了解初中数学课堂中学生参与情况，并按“主动质疑、独立思考、专注听讲、讲解题目”四个项目进行评价．检测小组随机抽查部分学校若干名学生，并将抽查学生的课堂参与情况绘制成如图所示的扇形统计图和条形统计图（均不完整）．请根据统计图中的信息解答下列问题：
（1）本次抽查的样本容量是 ；
（2）在扇形统计图中，“主动质疑”对应的圆心角为 度；
（3）将条形统计图补充完整；
（4）如果该地区初中学生共有60000名，那么在课堂中能“独立思考”的学生约有多少人？
18．为做好食堂的服务工作，某学校食堂对学生最喜爱的菜肴进行了抽样调查，下面试根据收集的数据绘制的统计图（不完整）：
（1）参加抽样调查的学生数是______人，扇形统计图中“大排”部分的圆心角是______°；
（2）把条形统计图补充完整；
（3）若全校有3000名学生，请你根据以上数据估计最喜爱“烤肠”的学生人数．
19．我市大力发展绿色交通，构建公共绿色交通体系，“共享单车”的投入使用给人们的出行带来便利．小明随机调查了若干市民租用共享单车的骑车时间t（单位：分），将获得的数据分成四组，绘制了如图统计图，请根据图中信息，解答下列问题：
（1）这次被调查的总人数是______；
（2）补全条形统计图；
（3）在扇形统计图中，求表示A组（t≤10分）的扇形圆心角的度数；
（4）如果骑共享单车的平均速度为12km/h，请估算，在租用共享单车的市民中，骑车路程不超过6km的人数所占的百分比．
20．随着科技的迅猛发展,人与人之间的沟通方式更多样、便捷某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题.
(1)这次统计共抽查了______名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为________;
(2)将条形统计图补充完整;
(3)该校共有2500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名
(4)某天甲、乙两名同学都想从“微信”“QQ”“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
21．为调查市民上班时最常用的交通工具的情况，随机抽取了四市部分市民进行调查,要求被调查者从“A：自行车，B：电动车，C：公交车，D：家庭汽车，E：其他”五个选项中选择最常用的一项，将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图，请结合统计图回答下列问题：
（1）在这次调查中，一共调查了 名市民．
（2）扇形统计图中，C组对应的扇形圆心角是 ．
（3）请补全条形统计图．
参考答案
1．B
【解析】试题解析：二月份用电量占第一季度用电量的百分比为： EMBED Equation.DSMT4
故选B.
2．C
【解析】反映2015年末嘉兴市各个县(区)常住人口占嘉兴市总人口的比例，宜采用扇形统计图，
故选：C.
3．B
【解析】试题解析：由题意可知：选择制陶的学生占的圆心角为
则
故选B.
4．D
【解析】试题解析：因为P、Q两国2016年财政经费支出的数额未知，所有A. B. C均错误.
故选D.
5．D
【解析】试题解析：
认为依情况而定的占27%，故A正确；
认为该扶的在统计图中所对应的圆心角是故B正确；
认为不该扶的占1 27% 65%=8%，故C正确；
认为该扶的占65%，故D错误；
故选D.
6．B
【解析】解：评委的分数是：（95+94+92+90+94）÷5=93（分），民主测评得分：50×70%×2+50×（1﹣10%﹣70%）×1=80（分），则综合得分是：93×0.4+80×0.6=85.2（分）．故选B．
点睛：本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
7．C
【解析】由统计图可知，选D的有10人占总人数的20%，
所以总人数为人，故D选项正确；
选A的有人，故A选项正确；
选B的有人，故B选项正确；
选C的有人，故C选项错误.
故选C.
8．C
【解析】试题解析：由条形图中可知乘车的人有25人，骑车的人有10人，
在扇形图中分析可知，乘车的占总数的50%，所以总数有25÷50%=50人，所以骑车人数占总人数的20%；
步行人数为0．×50=15人；乘车人数是骑车人数的2.5倍．
故选C．
点睛：在扇形统计图中，每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°比．
9．135°
【解析】由题意可得扇形C所对应的圆心角的度数为： .
故答案为：135°.
10．315
【解析】分析：用总人数乘以样本中出境游东南亚地区的百分比即可得．
详解：出境游东南亚地区的游客约有700×（1﹣16%﹣15%﹣11%﹣13%）=700×45%=315（万）．故答案为：315．
点睛：本题主要考查扇形统计图与样本估计总体，解题的关键是掌握各项目的百分比之和为1，利用样本估计总体思想的运用．
11．2
【解析】试题解析：从扇形统计图可以看出用于教育的支出所占的圆心角为
他家用于教育的支出的费用（万元）．
故答案为:2．
12．48
【解析】分析：利用共抽取作品数=C等级数÷对应的百分比，再用总数减去等级为A、C、D的作品数，即可求得等级为B的作品数.
详解： 30÷25%=120（份），
作品中等级为B的作品数120-36-30-6=48份.
故答案为：48.
点睛：本题主要考查了条形统计图，扇形统计图以及用样本估计总体，解题的关键是读懂统计图，能从统计图中获取准确的信息.
13．27
【解析】分析：根据统计图中的数据可以求得比赛总场数，从而可以求得足球队全年比赛胜的场数．
详解：由统计图可得，
比赛场数为：10÷20%=50，
胜的场数为：50×（1﹣26%﹣20%）=50×54%=27，
故答案为：27．
点睛：主要考查条形统计图和扇形统计图，找出它们之间的关系式解题的关键.
14．150
【解析】售出各种口味雪糕数量为200÷40%=500支，所以售出奶油口味雪糕的数量为500×30%=150支，故答案为150.
15． 7.5 108°
【解析】利用西红柿占总面积的比例以及西红柿的种植面积计算出蔬菜总面积为4.2÷56％=7.5；利用扇形统计图的特点，可知360°×30％=108°．
故答案为：7.5；108°.
点睛：此题主要考查的是如何观察扇形统计图并且从统计图中获取信息，然后再进行计算、解答即可．
16．(1) 200、108°、A (2)见解析 （3）480人
【解析】分析：(1)由C区域36°有20人求调查的人数；用调查的人数减去A区域和C区域的人数得B区域的人数，360°乘以B区域的人数除以调查的人数；由中位数的定义求；(2)见解析；(3)A，B区域的人数的和除以调查的人数乘以全校人数.
详解：(1)根据题意得：20÷＝200(名).
则本次共调查了200名学生；
∵B区域的人数为200﹣(120＋20)＝60(名)．
则B区域的圆心角度数为360°×＝108°；
由于第100.101个数据均落在A中，所以在抽查的学生中调查结果的中位数落在A(了解很多)中；
(2)补全条形图如下：
(3)1200×＝480，
答：估算该校不是了解很多的学生人数为480人．
点睛：本题主要考查了条形统计图与扇形统计图的综合运用及用列表法或画树状图法求概率，从条形统计图和扇形统计图中获取有用的信息是解决这类问题的关键.圆心角的度数＝部分占样本容量的百分比×360°＝部分÷样本容量×360°.
17．（1）560；（2）54 ； （3）见解析（4）在课堂中能“独立思考”的学生约有18000人
【解析】分析：(1)、根据“专心听讲”的人数和百分比得出样本容量；(2)、根据“主动质疑”的人数和样本容量得出所占的百分比，从而得出圆心角的度数；(3)、根据样本容量得出“讲解题目”的人数，然后进行补全；(4)、首先得出“独立思考”所占的百分比，然后得出答案．
详解：（1）560；
（2）54 ；
（3）在图中“讲解题目”画出相应的小长方形，并标注“84”(图略)；
（4）因为 “独立思考”的学生占总数的比例为168÷560=30%，
所以60000名七年级学生 中“独立思考”的约有60000×30%=18000（人），
答：在课堂中能“独立思考”的学生约有18000人.
点睛：本题主要考查的就是扇形统计图与条形统计图，属于基础题型．解答这个题目的关键就是要明白一个基本公式：频数=样本容量×频率．
18．（1）200，144；（2）答案见解析；（3）600.
【解析】分析：（1）根据喜爱鸡腿的人数是50人，所占的百分比是25%即可求得调查的总人数；
（2）利用调查的总人数减去其它组的人数即可求得喜爱烤肠的人数；
（3）利用总人数3000乘以对应的比例即可求解．
详解：（1）参加调查的人数是：50÷25%=200（人），扇形统计图中“大排”部分的圆心角的度数是：360×=144°．
故答案为：200，144；
（2）喜爱烤肠的人数是：200﹣80﹣50﹣30=40（人），补充条形统计图如下：
（3）估计最喜爱“烤肠”的学生人数是：3000×=600（人）．
点睛：本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
19．50
【解析】分析：(1)、根据B的人数和百分比得出总人数；(2)、根据总人数求出C组的人数；(3)、根据A组的人数和总人数的比值得出圆心角的度数；(4)、首先求出6km所需要的时间，然后得出小于30分钟的人数，从而求出所占的百分比．
详解：（1）这次被调查的总人数是19÷38﹪=50（人）；
（2）C组人数为50-（15+19+4）=12（人）；
补全条形统计图；
（3）求表示A组（t≤10分）的扇形圆心角的度数为；
（4）路程是6km时所用的时间是：6÷12=0.5（小时）=30（分钟），则骑车路程不超过6km的人数所占的百分比是：．
点睛：本题主要考查的就是条形统计图和扇形统计图，属于中等难度题型．在解答这种问题的时候，我们必须要明确一个公式：频数=样本容量×频率，根据这个公式就可以求出答案．
20．(1)100,108°;(2)补图见解析;(3) 1000人; (4)树状图见解析,甲、乙两名同学恰好选中同一种沟通方式的概率为:.
【解析】分析：(1)用电话的有20人占抽查人数的20%求抽查的人数；用QQ的人数占抽查总人数的比乘以360°；(2)用抽查的人数乘以5%即为用短信的人数，由此求出用微信的人数，即可补充条形图；(3)用抽查学生中用微信人数占抽查人数的比乘以全校学生数可求；(4)列树状图求出总的情况和符合条件的情况.
详解：(1)这次统计共抽查了20÷20%＝100名；
在扇形统计图中，表示“QQ”的扇形圆心角的度数为×360＝108°.
故答案为100108°.
(2)喜欢用短信的人数为:100×5%＝5名，喜欢用微信的人数为:100－20－5－30－5＝40名.
补充图形如下：
(3)因为该校共有2500名学生，所以估计该校最喜欢用“微信”进行沟通的学生有×2500＝1000名.
(4)列出树状图，如图所示
共有9种情况，其中两人恰好选中同一种沟通方式共有3种情况，
所以甲，乙两名同学恰好选中同一种沟通方式的概率为:，
点睛：本题主要考查了条形统计图与扇形统计图的综合运用及用列表法或画树状图法求概率，从条形统计图和扇形统计图中获取有用的信息是解决这类问题的关键，扇形圆心角的度数＝部分占样本容量的百分比×360°＝部分÷样本容量×360°，在等可能事件中，如果所有等可能的结果为n，而其中所包含的事件A可能出现的结果数是m，那么事件A的概率为.
21．（1）2000；（2）108°；（3）图见解析.
【解析】试题分析：（1）根据B组的人数以及百分比，即可得到被调查的人数，
（2）由总人数减去A、B、D、E组的人数，即可得出C组的人数，再根据扇形圆心角的度数=部分占总体的百分比×360°进行计算即可；
（3）根据C组的人数，补全条形统计图．
试题解析：解：（1）被调查的人数为：800÷40%=2000（人）
（2）C组的人数为：2000﹣100﹣800﹣200﹣300=600（人），∴C组对应的扇形圆心角度数为： ×360°=108°；
（3）条形统计图如下：
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)