1.2 同位角、内错角、同旁内角同步练习

中小学教育资源及组卷应用平台


绝密★启用前
浙教版七年级下同步练习第一章平行线
1.2同位角、内错角、同旁内角
题号 一 二 三 总分
得分
注意事项：
1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上
第Ⅰ卷（选择题）
请点击修改第I卷的文字说明
评卷人 得 分

一．选择题（共8小题）
1．如图，∠B的同位角可以是（　　）

A．∠1 B．∠2 C．∠3 D．∠4
2．如图，直线AD，BE被直线BF和AC所截，则∠1的同位角和∠5的内错角分别是（　　）

A．∠4，∠2 B．∠2，∠6 C．∠5，∠4 D．∠2，∠4
3．如图，下列说法中不正确的是（　　）

A．∠1和∠3是同旁内角 B．∠2和∠3是内错角
C．∠2和∠4是同位角 D．∠3和∠5是对顶角
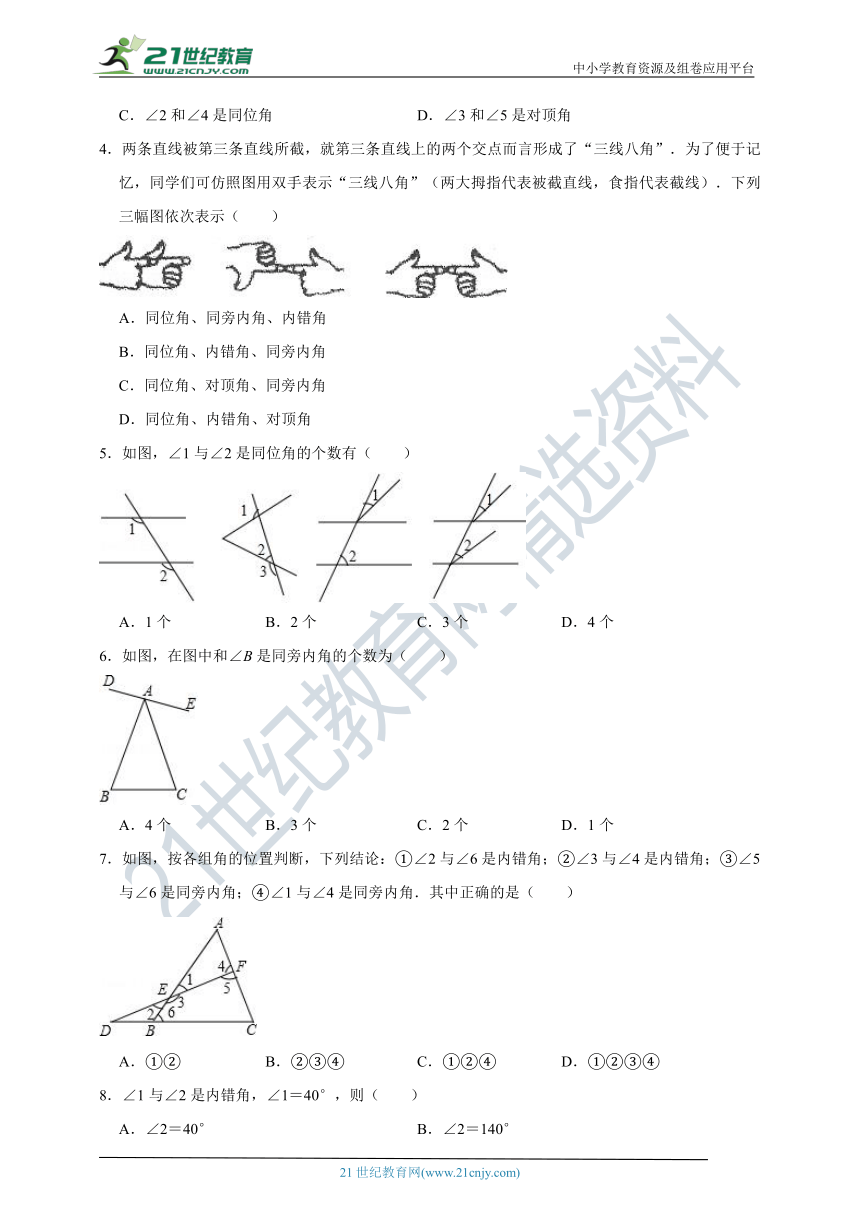
4．两条直线被第三条直线所截，就第三条直线上的两个交点而言形成了“三线八角”．为了便于记忆，同学们可仿照图用双手表示“三线八角”（两大拇指代表被截直线，食指代表截线）．下列三幅图依次表示（　　）

A．同位角、同旁内角、内错角
B．同位角、内错角、同旁内角
C．同位角、对顶角、同旁内角
D．同位角、内错角、对顶角
5．如图，∠1与∠2是同位角的个数有（　　）

A．1个 B．2个 C．3个 D．4个
6．如图，在图中和∠B是同旁内角的个数为（　　）

A．4个 B．3个 C．2个 D．1个
7．如图，按各组角的位置判断，下列结论：①∠2与∠6是内错角；②∠3与∠4是内错角；③∠5与∠6是同旁内角；④∠1与∠4是同旁内角．其中正确的是（　　）

A．①② B．②③④ C．①②④ D．①②③④
8．∠1与∠2是内错角，∠1＝40°，则（　　）
A．∠2＝40° B．∠2＝140°
C．∠2＝40°或∠2＝140° D．∠2的大小不确定



第Ⅱ卷（非选择题）
请点击修改第Ⅱ卷的文字说明
评卷人 得 分

二．填空题（共6小题）
9．如图，写出图中∠A所有的内错角：　 　．

10．两条直线被第三条直线所截，∠2是∠3的同旁内角，∠1是∠3的内错角，若∠2＝4∠3，∠3＝2∠1，则∠1的度数是　 　．
11．如图，射线DE、DC被直线AB所截得的用数字表示的角中，∠4与　 　是同位角，∠4与　 　是内错角，∠4与　 　是同旁内角．

12．如图1，三条直线两两相交，且不共点，则图中同旁内角有　 　对；如图2，四条直线两两相交，任三条直线不经过同一点，则图中的同旁内角有　 　对．

13．如图填空．
（1）若ED，BC被AB所截，则∠1与　 　是同位角．
（2）若ED，BC被AF所截，则∠3与　 　是内错角．
（3）∠1 与∠3是AB和AF被　 　所截构成的　 　角．
（4）∠2与∠4是　 　和　 　被BC所截构成的　 　角．

14．如图，如果∠1＝50°，∠2＝100°，那么∠3的同位角等于　 　，∠3的内错角等于　 　，∠3的同旁内角等于　 　．

评卷人 得 分

三．解答题（共6小题）
15．如图，直线DE经过点A．
（1）写出∠B的内错角是　 　，同旁内角是　 　．
（2）若∠EAC＝∠C，AC平分∠BAE，∠B＝44°，求∠C的度数．

16．已知：如图是一个跳棋棋盘，其游戏规则是：一个棋子从某一个起始角开始，经过若干步跳动以后，到达终点角．跳动时，每一步只能跳到它的同位角或内错角或同旁内角的位置上，例如：从起始位置∠1跳到终点位置∠3写出其中两种不同路径，路径1：∠1﹣同旁内角→∠9﹣内错角→∠3．
路径2：∠1一内错角→∠12一内错角→∠6﹣同位角→∠10﹣同旁内角→∠3．
试一试：（1）从起始∠1跳到终点角∠8；
（2）从起始角∠1依次按同位角、内错角、同旁内角的顺序跳，能否跳到终点∠8？

17．读图1～图4，回答下列问题．
（1）请你写出图1、图2、图3和图4中分别有几对同旁内角？
（2）观察图形，请写出图n（n是正整数）中有几对同旁内角？
18．如图，已知直线EF与AB交于点M，与CD交于点O，OG平分∠DOF，若∠COM＝120°，∠EMB＝∠COF．
（1）求∠FOG的度数；
（2）写出一个与∠FOG互为同位角的角；
（3）求∠AMO的度数．

19．如图，已知直线a，b被直线c，d所截，直线a，c，d相交于点O，按要求完成下列各小题．
（1）在图中的∠1～∠9这9个角中，同位角共有多少对？请你全部写出来；
（2）∠4和∠5是什么位置关系的角？∠6和∠8之间的位置关系与∠4和∠5的相同吗？

20．如图，有四条互相不平行的直线L1、L2、L3、L4所截出的八个角．请你任意选择其中的三个角（不可选择未标注的角），尝试找到它们的关系，并选择其中一组予以证明．




参考答案与试题解析
一．选择题（共8小题）
1．如图，∠B的同位角可以是（　　）

A．∠1 B．∠2 C．∠3 D．∠4
【分析】直接利用两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角，进而得出答案．
【解答】解：∠B的同位角可以是：∠4．
故选：D．
【点评】此题主要考查了同位角的定义，正确把握定义是解题关键．
2．如图，直线AD，BE被直线BF和AC所截，则∠1的同位角和∠5的内错角分别是（　　）

A．∠4，∠2 B．∠2，∠6 C．∠5，∠4 D．∠2，∠4
【分析】根据同位角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角进行分析即可．
根据内错角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角进行分析即可．
【解答】解：∠1的同位角是∠2，∠5的内错角是∠6，
故选：B．
【点评】此题主要考查了三线八角，关键是掌握同位角的边构成“F“形，内错角的边构成“Z“形，同旁内角的边构成“U”形．
3．如图，下列说法中不正确的是（　　）

A．∠1和∠3是同旁内角 B．∠2和∠3是内错角
C．∠2和∠4是同位角 D．∠3和∠5是对顶角
【分析】直接利用同旁内角、内错角、同位角、对顶角的定义分别分析得出答案．
【解答】解：A、∠1和∠3是同旁内角，正确，不合题意；
B、∠2和∠3是内错角，正确，不合题意；
C、∠2和∠4是同位角，错误，符合题意；
D、∠3和∠5是对顶角，正确，不合题意；
故选：C．
【点评】此题主要考查了同旁内角、内错角、同位角、对顶角的定义，正确把握相关定义是解题关键．
4．两条直线被第三条直线所截，就第三条直线上的两个交点而言形成了“三线八角”．为了便于记忆，同学们可仿照图用双手表示“三线八角”（两大拇指代表被截直线，食指代表截线）．下列三幅图依次表示（　　）

A．同位角、同旁内角、内错角
B．同位角、内错角、同旁内角
C．同位角、对顶角、同旁内角
D．同位角、内错角、对顶角
【分析】两条线a、b被第三条直线c所截，在截线的同旁，被截两直线的同一方，把这种位置关系的角称为同位角；
两个角分别在截线的异侧，且夹在两条被截线之间，具有这样位置关系的一对角互为内错角；
两个角都在截线的同一侧，且在两条被截线之间，具有这样位置关系的一对角互为同旁内角．
据此作答即可．
【解答】解：根据同位角、内错角、同旁内角的概念，可知
第一个图是同位角，第二个图是内错角，第三个图是同旁内角．
故选：B．
【点评】本题考查了同位角、内错角、同旁内角，解题的关键是掌握同位角、内错角、同旁内角，并能区别它们．
5．如图，∠1与∠2是同位角的个数有（　　）

A．1个 B．2个 C．3个 D．4个
【分析】根据同位角的定义：在截线的同侧，并且在被截线的同一方的两个角是同位角．
【解答】解：这四个图中，∠1与∠2有一条边在同一条直线上，另一条边在被截线的同一方，是同位角．
故选：D．
【点评】本题考查了同位角、内错角、同旁内角．解答此类题确定三线八角是关键，可直接从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．
6．如图，在图中和∠B是同旁内角的个数为（　　）

A．4个 B．3个 C．2个 D．1个
【分析】根据同旁内角的定义找出即可．
【解答】解：在图中和∠B是同旁内角的是∠BAC，∠C，∠BAE，共3个，
故选：B．
【点评】本题考查了同位角，内错角，同旁内角的定义，能熟记同旁内角的定义的内容是解此题的关键．
7．如图，按各组角的位置判断，下列结论：①∠2与∠6是内错角；②∠3与∠4是内错角；③∠5与∠6是同旁内角；④∠1与∠4是同旁内角．其中正确的是（　　）

A．①② B．②③④ C．①②④ D．①②③④
【分析】根据同位角、内错角、同旁内角的定义进行解答即可．
【解答】解：①∠2与∠6是内错角，说法正确；
②∠3与∠4是内错角，说法正确；
③∠5与∠6是同旁内角，说法错误；
④∠1与∠4是同旁内角，说法正确．
故选：C．
【点评】此题主要考查了同位角、内错角、同旁内角，解题的关键是熟记同位角、内错角、同旁内角的定义．
8．∠1与∠2是内错角，∠1＝40°，则（　　）
A．∠2＝40° B．∠2＝140°
C．∠2＝40°或∠2＝140° D．∠2的大小不确定
【分析】两直线平行时内错角相等，不平行时无法确定内错角的大小关系．
【解答】解：内错角只是一种位置关系，并没有一定的大小关系，只有两直线平行时，内错角才相等．
故选：D．
【点评】特别注意，内错角相等的条件是两直线平行．
二．填空题（共6小题）
9．如图，写出图中∠A所有的内错角：　∠ACD，∠ACE　．

【分析】内错角就是：两个角在截线的两旁，又分别处在被截的两条直线内侧的位置的角．
【解答】解：根据内错角的定义，图中∠A所有的内错角：∠ACD，∠ACE．
故答案为∠ACD、∠ACE．
【点评】考查了同位角、内错角、同旁内角．解答此类题确定三线八角是关键，可直接从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．
10．两条直线被第三条直线所截，∠2是∠3的同旁内角，∠1是∠3的内错角，若∠2＝4∠3，∠3＝2∠1，则∠1的度数是　20°　．
【分析】设∠1＝x°，则∠3＝2x°，∠2＝8x°，根据邻补角互补可得方程，求解即可．
【解答】解：如图，设∠1＝x°，则∠3＝2x°，∠2＝4∠3＝8x°，

∵∠1+∠2＝180°，
∴x°+8x°＝180，
解得：x＝20°，
∴∠1＝20°．
故答案为：20°．
【点评】本题考查了同位角、内错角、同旁内角以及角的计算，解决问题的关键是掌握：内错角的边构成“Z“形，同旁内角的边构成“U”形．
11．如图，射线DE、DC被直线AB所截得的用数字表示的角中，∠4与　∠1　是同位角，∠4与　∠2　是内错角，∠4与　∠5　是同旁内角．

【分析】同位角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角．
内错角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角．
同旁内角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角．
【解答】解：如图，射线DE、DC被直线AB所截得的用数字表示的角中，∠4与∠1是同位角，∠4与∠2是内错角，∠4与∠5是同旁内角．
故答案为：∠1，∠2，∠5．
【点评】本题考查了同位角、内错角、同旁内角．解答此类题确定三线八角是关键，可直接从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．
12．如图1，三条直线两两相交，且不共点，则图中同旁内角有　6　对；如图2，四条直线两两相交，任三条直线不经过同一点，则图中的同旁内角有　24　对．

【分析】如图1，按两条直线被第三条直线所截，得出同旁内角的对数，发现可以形成6对同旁内角；如，图2，根据总结出的结论得出．
【解答】解：如图1，直线EF与直线AB被直线CD所截时，所构成的同旁内角有：∠1与∠2，∠2与∠3，
同理，每一条直线做截线时，都有两对同旁内角，所以一共有6对同旁内角；
如图2，不交于同一点的四条直线两两相交，设这四条直线分别为a、b、c、d，
可以分为：
①a、b、c；
②a、b、d；
③a、c、d；
④b、c、d，每三条直线都构成了6对同旁内角，所以这四组线中一共有24对同旁内角；
故答案为：6，24．


【点评】本题考查了同位角、内错角、同旁内角．解答此类题确定三线八角是关键，可直接从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．
13．如图填空．
（1）若ED，BC被AB所截，则∠1与　∠2　是同位角．
（2）若ED，BC被AF所截，则∠3与　∠4　是内错角．
（3）∠1 与∠3是AB和AF被　ED　所截构成的　内错　角．
（4）∠2与∠4是　AB　和　AF　被BC所截构成的　同位　角．

【分析】根据同位角、内错角的定义进行分析解答即可，两个角分别在截线的两侧，且在两条直线之间，具有这样位置关系的一对角互为内错角，两个角都在截线的同旁，又分别处在被截的两条线的同侧，具有这样位置关系的一对角叫做同位角．
【解答】解：（1）如图：若ED，BC被AB所截，则∠1与∠2是同位角，

（2）若ED，BC被AF所截，则∠3与∠4是内错角，

（3）∠1 与∠3是AB和AF被ED所截构成的内错角，

（4）∠2与∠4是AB和AF被BC所截构成的同位角．
故答案为∠2；∠4；ED，内错；AB，AF，同位．
【点评】本题主要考查内错角、同位角的定义，解答此类题确定三线八角是关键，可直接从截线入手．
14．如图，如果∠1＝50°，∠2＝100°，那么∠3的同位角等于　80°　，∠3的内错角等于　80°　，∠3的同旁内角等于　100°　．

【分析】根据同位角，内错角，同旁内角的定义，利用对顶角相等，邻补角的和等于180°计算即可得解．
【解答】解：如图，∵∠2＝100°，
∴∠3的同位角∠4＝180°﹣100°＝80°，
∠3的内错角∠5＝∠4＝80°，
∠3的同旁内角∠6＝∠2＝100°．
故答案为：80°，80°，100°．

【点评】本题考查了同位角、内错角、同旁内角的定义，对顶角相等的性质，邻补角的和等于180°，熟记定义并准确识图是解题的关键．
三．解答题（共6小题）
15．如图，直线DE经过点A．
（1）写出∠B的内错角是　∠BAD　，同旁内角是　∠BAC，∠EAB和∠C　．
（2）若∠EAC＝∠C，AC平分∠BAE，∠B＝44°，求∠C的度数．

【分析】（1）根据内错角和同旁内角的概念解答即可；
（2）根据平行线的判定和性质解答即可．
【解答】解：（1）∠B的内错角是∠BAD，∠B的同旁内角是∠BAC，∠EAB和∠C；
（2）∵∠EAC＝∠C，
∴DE∥BC，
∴∠BAE＝180°﹣44°＝136°，
∵AC平分∠BAE，
∴∠EAC＝68°，
∴∠C＝∠EAC＝68°，
故答案为：∠BAD；∠BAC，∠EAB和∠C
【点评】本题主要考查平行线的性质，掌握平行线的性质和判定是解题的关键，即①两直线平行?同位角相等，②两直线平行?内错角相等，③两直线平行?同旁内角互补，④a∥b，b∥c?a∥c．
16．已知：如图是一个跳棋棋盘，其游戏规则是：一个棋子从某一个起始角开始，经过若干步跳动以后，到达终点角．跳动时，每一步只能跳到它的同位角或内错角或同旁内角的位置上，例如：从起始位置∠1跳到终点位置∠3写出其中两种不同路径，路径1：∠1﹣同旁内角→∠9﹣内错角→∠3．
路径2：∠1一内错角→∠12一内错角→∠6﹣同位角→∠10﹣同旁内角→∠3．
试一试：（1）从起始∠1跳到终点角∠8；
（2）从起始角∠1依次按同位角、内错角、同旁内角的顺序跳，能否跳到终点∠8？

【分析】（1）路径：∠1→∠12→∠8；
（2）路径：∠1→∠10→∠5→∠8．
【解答】解：（1）路径∠1∠12∠8；

（2）从起始角∠1依次按同位角、内错角、同旁内角的顺序跳，能跳到终点∠8．其路径为：
路径：∠1∠10∠5∠8．
【点评】考查了同位角、内错角、同旁内角．解答此类题确定三线八角是关键，可直接从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．
17．读图1～图4，回答下列问题．
（1）请你写出图1、图2、图3和图4中分别有几对同旁内角？
（2）观察图形，请写出图n（n是正整数）中有几对同旁内角？
【分析】根据同旁内角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角进行分析即可，进而求出每个图形中同旁内角的个数，进而得出答案．
【解答】解：（1）图1中：有2对同旁内角；图2中：有8对同旁内角；
图3中：有18对同旁内角；图4中：有32对同旁内角；
（2）图n（n是正整数）中有2n2对同旁内角．
【点评】此题主要考查了三线八角，关键是掌握同旁内角的边构成“U”形．
18．如图，已知直线EF与AB交于点M，与CD交于点O，OG平分∠DOF，若∠COM＝120°，∠EMB＝∠COF．
（1）求∠FOG的度数；
（2）写出一个与∠FOG互为同位角的角；
（3）求∠AMO的度数．

【分析】（1）根据对顶角相等可得∠DOF的度数，再根据角平分线的定义可求∠FOG的度数；
（2）根据同位角的定义可求与∠FOG互为同位角的角；
（3）根据邻补角的性质可求∠COF，再根据已知条件和对顶角相等可求∠AMO的度数．
【解答】解：（1）∵∠COM＝120°，
∴∠DOF＝120°，
∵OG平分∠DOF，
∴∠FOG＝60°；

（2）与∠FOG互为同位角的角是∠BMF；

（3）∵∠COM＝120°，
∴∠COF＝60°，
∵∠EMB＝∠COF，
∴∠EMB＝30°，
∴∠AMO＝30°．
【点评】本题考查了同位角的定义，角平分线定义，对顶角、邻补角定义的应用，能综合运用知识点进行推理和计算是解此题的关键．
19．如图，已知直线a，b被直线c，d所截，直线a，c，d相交于点O，按要求完成下列各小题．
（1）在图中的∠1～∠9这9个角中，同位角共有多少对？请你全部写出来；
（2）∠4和∠5是什么位置关系的角？∠6和∠8之间的位置关系与∠4和∠5的相同吗？

【分析】（1）直接利用两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角，进而得出答案；
（2）直接利用两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角，进而得出答案．
【解答】解：（1）如图所示：同位角共有5对：
分别是∠1和∠5，∠2和∠3，∠3和∠7，∠4和∠6，∠4和∠9；

（2）∠4和∠5是同旁内角，∠6和∠8也是同旁内角，故∠6和∠8之间的位置关系与∠4和∠5的相同．
【点评】此题主要考查了同位角以及同旁内角的定义，正确把握相关定义是解题关键．
20．如图，有四条互相不平行的直线L1、L2、L3、L4所截出的八个角．请你任意选择其中的三个角（不可选择未标注的角），尝试找到它们的关系，并选择其中一组予以证明．

【分析】根据三角形的外角和为360°，三角形的内角和为180°以及三角形外角和定理即可写出三个角之间的数量关系．
【解答】解：如∠2+∠4+∠6＝360°，∠1+∠5+∠7＝180°，∠2＝∠5+∠7，∠3＝∠1+∠8，
已知如图：有四条互相不平行的直线L1、L2、L3、L4所截出的八个角，
求证：∠1+∠5+∠7＝180°，
证明：∵∠DAC+∠7+∠5＝180°，
又∵∠1＝∠DAC，
∴∠1+∠5+∠7＝180°．
【点评】此题主要考查了对顶角的性质以及三角形的内角和定理，正确的应用三角形内角和定理是解决问题的关键．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布
日期：2019/1/29 9:23:27；用户：zhrasce20；邮箱：zhrasce20@163.com；学号：6322261














































21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）



HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)