1.3 平行线的判定同步练习

中小学教育资源及组卷应用平台


绝密★启用前
浙教版七年级下同步练习第一章平行线
1.3 平行线的判定
题号 一 二 三 总分
得分
注意事项：
1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上
第Ⅰ卷（选择题）
请点击修改第I卷的文字说明
评卷人 得 分

一．选择题（共8小题）
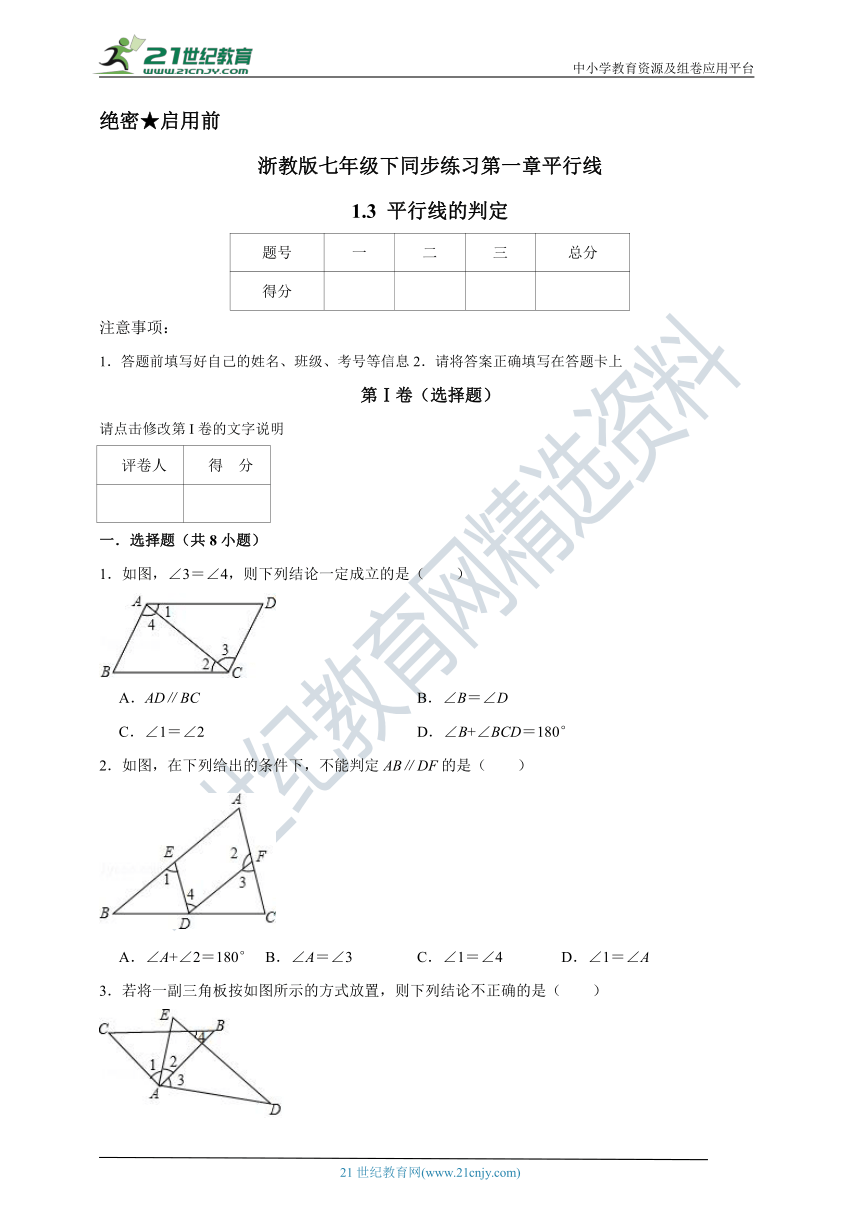
1．如图，∠3＝∠4，则下列结论一定成立的是（　　）

A．AD∥BC B．∠B＝∠D
C．∠1＝∠2 D．∠B+∠BCD＝180°
2．如图，在下列给出的条件下，不能判定AB∥DF的是（　　）

A．∠A+∠2＝180° B．∠A＝∠3 C．∠1＝∠4 D．∠1＝∠A
3．若将一副三角板按如图所示的方式放置，则下列结论不正确的是（　　）

A．∠1＝∠3 B．如果∠2＝30°，则有AC∥DE
C．如果∠2＝30°，则有BC∥AD D．如果∠2＝30°，必有∠4＝∠C
4．如图，下列能判定AB∥EF的条件有（　　）
①∠B+∠BFE＝180°
②∠1＝∠2
③∠3＝∠4
④∠B＝∠5．

A．1个 B．2个 C．3个 D．4个
5．同一平面内的四条直线若满足a⊥b，b⊥c，c⊥d，则下列式子成立的是（　　）
A．a∥d B．b⊥d C．a⊥d D．b∥c
6．如图，直线a，b被直线c所截，现给出下列四个条件：
①∠1＝∠5；②∠4＝∠7，
③∠2+∠3＝180°；④∠3＝∠5；
其中能判定a∥b的条件的序号是（　　）

A．①② B．①③ C．①④ D．③④
7．如图，在下列条件中：①∠1＝∠2；②∠BAD＝∠BCD；③∠ABC＝∠ADC且∠3＝∠4；④∠BAD+∠ABC＝180°，能判定AB∥CD的有（　　）

A．3个 B．2个 C．1个 D．0个
8．已知在同一平面内，有三条直线a，b，c，若a∥b，b∥c，则直线a与直线c之间的位置关系是（　　）
A．相交 B．平行 C．垂直 D．平行或相交



第Ⅱ卷（非选择题）
请点击修改第Ⅱ卷的文字说明
评卷人 得 分

二．填空题（共6小题）
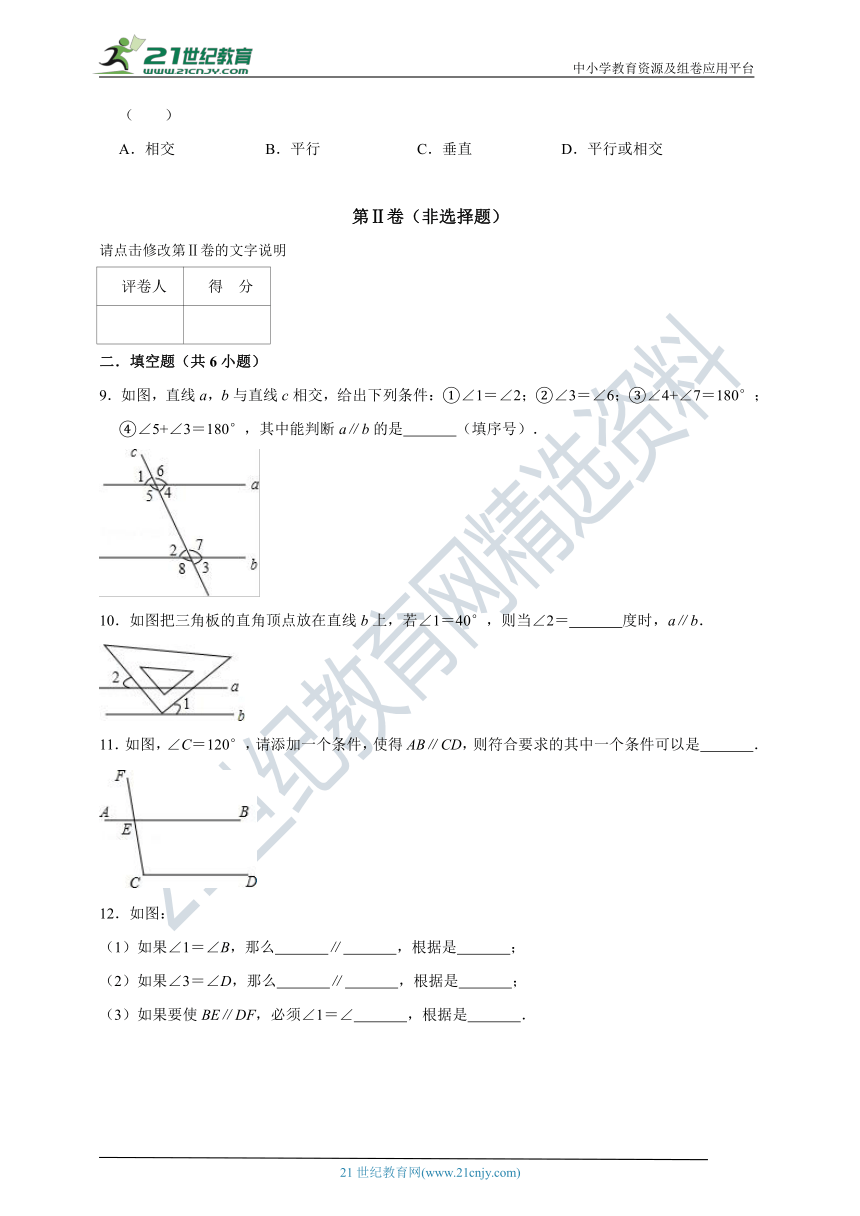
9．如图，直线a，b与直线c相交，给出下列条件：①∠1＝∠2；②∠3＝∠6；③∠4+∠7＝180°；④∠5+∠3＝180°，其中能判断a∥b的是　 　（填序号）．

10．如图把三角板的直角顶点放在直线b上，若∠1＝40°，则当∠2＝　 　度时，a∥b．

11．如图，∠C＝120°，请添加一个条件，使得AB∥CD，则符合要求的其中一个条件可以是　 　．

12．如图：
（1）如果∠1＝∠B，那么　 　∥　 　，根据是　 　；
（2）如果∠3＝∠D，那么　 　∥　 　，根据是　 　；
（3）如果要使BE∥DF，必须∠1＝∠　 　，根据是　 　．

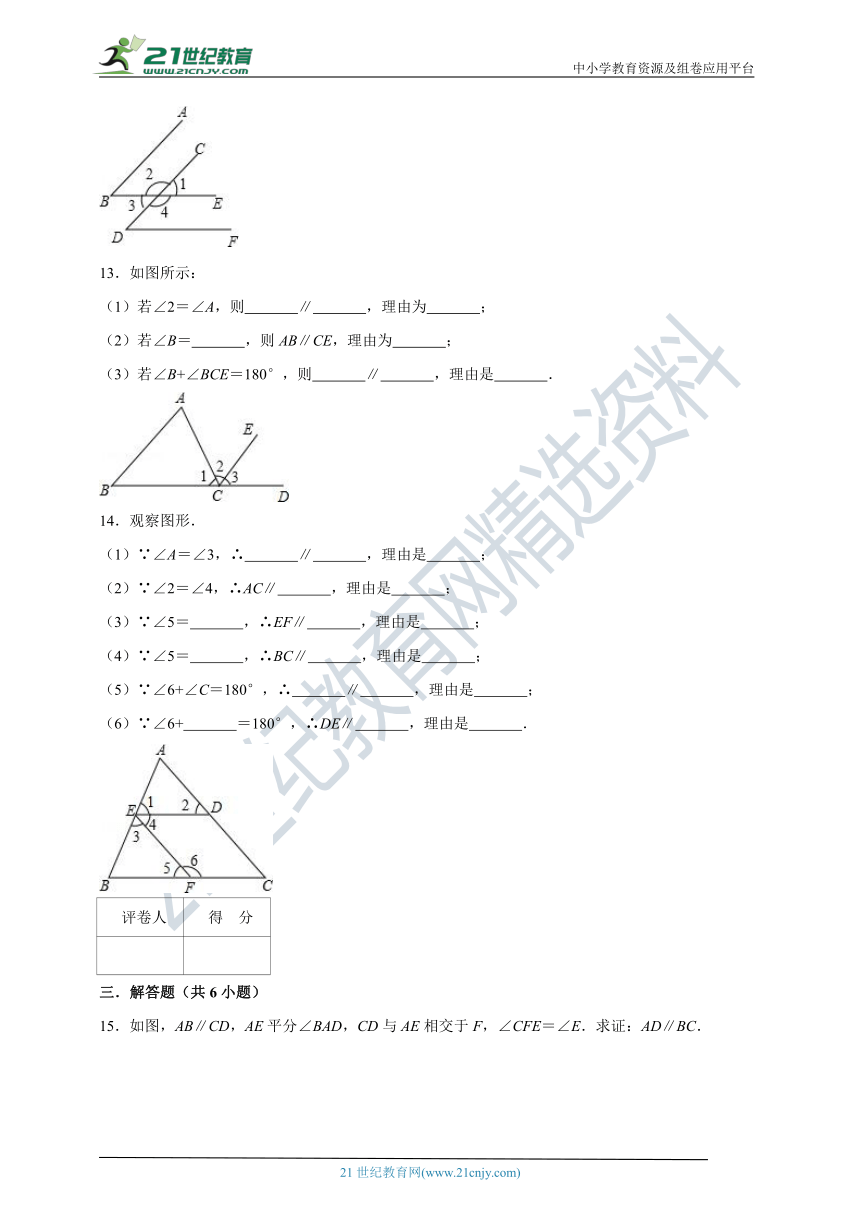
13．如图所示：
（1）若∠2＝∠A，则　 　∥　 　，理由为　 　；
（2）若∠B＝　 　，则AB∥CE，理由为　 　；
（3）若∠B+∠BCE＝180°，则　 　∥　 　，理由是　 　．

14．观察图形．
（1）∵∠A＝∠3，∴　 　∥　 　，理由是　 　；
（2）∵∠2＝∠4，∴AC∥　 　，理由是　 　；
（3）∵∠5＝　 　，∴EF∥　 　，理由是　 　；
（4）∵∠5＝　 　，∴BC∥　 　，理由是　 　；
（5）∵∠6+∠C＝180°，∴　 　∥　 　，理由是　 　；
（6）∵∠6+　 　＝180°，∴DE∥　 　，理由是　 　．

评卷人 得 分

三．解答题（共6小题）
15．如图，AB∥CD，AE平分∠BAD，CD与AE相交于F，∠CFE＝∠E．求证：AD∥BC．

16．如图，AD∥BC，∠EAD＝∠C，∠FEC＝∠BAE，∠EFC＝50°
（1）求证：AE∥CD；
（2）求∠B的度数．

17．填写推理理由：
如图，CD∥EF，∠1＝∠2，求证：∠3＝∠ACB．
证明：∵CD∥EF，
∴∠DCB＝∠2　 　
∵∠1＝∠2，∴∠DCB＝∠1．　 　
∴GD∥CB　 　．
∴∠3＝∠ACB　 　．

18．如图，BE平分∠ABD，DE平分∠BDC，且∠1+∠2＝90°．
求证：AB∥CD．

19．完成下面的解题过程，并在括号内填上依据．
如图，∠AHF+∠FMD＝180°，GH平分∠AHF，MN平分∠DME．
求证：GH∥MN．
证明：∵∠AHF+∠FMD＝180°，　 　+∠FMD＝180°，
∴　 　．
∵GH平分∠AHF，MN平分∠DME，
∴∠1＝∠AHF，∠2＝∠DME　 　．
∴∠1＝∠2　 　．
∴GH∥MN　 　．

20．如图，已知∠1＝60°，∠2＝60°，∠MAE＝45°，∠FEG＝15°，EG平分∠AEC，∠NCE＝75°．求证：
（1）AB∥EF．
（2）AB∥ND．




参考答案与试题解析
一．选择题（共8小题）
1．如图，∠3＝∠4，则下列结论一定成立的是（　　）

A．AD∥BC B．∠B＝∠D
C．∠1＝∠2 D．∠B+∠BCD＝180°
【分析】根据内错角相等两直线平行可得AB∥CD，再根据平行线的性质可得∠B+∠BCD＝180°．
【解答】解：∵∠3＝∠4，
∴AB∥CD，
∴∠B+∠BCD＝180°，
故选：D．
【点评】此题主要考查了平行线的判定和性质，关键是掌握两条直线被第三条所截，如果内错角相等，那么这两条直线平行．
2．如图，在下列给出的条件下，不能判定AB∥DF的是（　　）

A．∠A+∠2＝180° B．∠A＝∠3 C．∠1＝∠4 D．∠1＝∠A
【分析】根据平行线的判定定理对各选项进行逐一判断即可．
【解答】解：A、∵∠A+∠2＝180°，∴AB∥DF，故本选项错误；
B、∵∠A＝∠3，∴AB∥DF，故本选项错误；
C、∵∠1＝∠4，∴AB∥DF，故本选项错误；
D、∵∠1＝∠A，∴AC∥DE，故本选项正确．
故选：D．
【点评】本题考查的是平行线的判定，熟知平行线的判定定理是解答此题的关键．
3．若将一副三角板按如图所示的方式放置，则下列结论不正确的是（　　）

A．∠1＝∠3 B．如果∠2＝30°，则有AC∥DE
C．如果∠2＝30°，则有BC∥AD D．如果∠2＝30°，必有∠4＝∠C
【分析】根据两种三角板的各角的度数，利用平行线的判定与性质结合已知条件对各个结论逐一验证，即可得出答案．
【解答】解：∵∠CAB＝∠EAD＝90°，
∴∠1＝∠CAB﹣∠2，∠3＝∠EAD﹣∠2，
∴∠1＝∠3．
∴（A）正确．
∵∠2＝30°，
∴∠1＝90°﹣30°＝60°，
∵∠E＝60°，
∴∠1＝∠E，
∴AC∥DE．
∴（B）正确．
∵∠2＝30°，
∴∠3＝90°﹣30°＝60°，
∵∠B＝45°，
∴BC不平行于AD．
∴（C）错误．
由AC∥DE可得∠4＝∠C．
∴（D）正确．
故选：C．

【点评】此题主要考查了学生对平行线判定与性质、余角和补角的理解和掌握，解答此题时要明确两种三角板各角的度数．
4．如图，下列能判定AB∥EF的条件有（　　）
①∠B+∠BFE＝180°
②∠1＝∠2
③∠3＝∠4
④∠B＝∠5．

A．1个 B．2个 C．3个 D．4个
【分析】根据平行线的判定定理对各小题进行逐一判断即可．
【解答】解：①∵∠B+∠BFE＝180°，∴AB∥EF，故本小题正确；
②∵∠1＝∠2，∴DE∥BC，故本小题错误；
③∵∠3＝∠4，∴AB∥EF，故本小题正确；
④∵∠B＝∠5，∴AB∥EF，故本小题正确．
故选：C．
【点评】本题考查的是平行线的判定，熟知平行线的判定定理是解答此题的关键．
5．同一平面内的四条直线若满足a⊥b，b⊥c，c⊥d，则下列式子成立的是（　　）
A．a∥d B．b⊥d C．a⊥d D．b∥c
【分析】根据同一平面内，垂直于同一条直线的两条直线平行，可证a∥c，再结合c⊥d，可证a⊥d．
【解答】解：∵a⊥b，b⊥c，
∴a∥c，
∵c⊥d，
∴a⊥d．故选C．
【点评】此题主要考查了平行线及垂线的性质．
6．如图，直线a，b被直线c所截，现给出下列四个条件：
①∠1＝∠5；②∠4＝∠7，
③∠2+∠3＝180°；④∠3＝∠5；
其中能判定a∥b的条件的序号是（　　）

A．①② B．①③ C．①④ D．③④
【分析】根据平行线的判定定理对各小题进行逐一分析即可．
【解答】解：①∵∠1＝∠5，∴a∥b，故本小题正确；
②∠4＝∠7不符合平行线的判定定理，故本小题错误；
③∠2+∠3＝180°不符合平行线的判定定理，故本小题错误；
④∵∠3＝∠5，∴a∥b，符合平行线的判定定理，故本小题正确．
故选：C．
【点评】本题考查的是平行线的判定，用到的知识点为：同位角相等，两直线平行；内错角相等，两直线平行．
7．如图，在下列条件中：①∠1＝∠2；②∠BAD＝∠BCD；③∠ABC＝∠ADC且∠3＝∠4；④∠BAD+∠ABC＝180°，能判定AB∥CD的有（　　）

A．3个 B．2个 C．1个 D．0个
【分析】①由∠1＝∠2，利用内错角相等两直线平行得到AD∥BC，本选项不合题意；②由∠BAD＝∠BCD，不能判定出平行，本选项不合题意；③由∠ABC＝∠ADC且∠3＝∠4，利用等式的性质一对内错角相等，进而得到AB∥CD，本选项符合题意；④由∠BAD+∠ABC＝180°，利用同旁内角互补得到AD∥BC，本选项不合题意．
【解答】解：①由∠1＝∠2，得到AD∥BC，本选项不合题意；②由∠BAD＝∠BCD，不能判定出平行，本选项不合题意；③由∠ABC＝∠ADC且∠3＝∠4，得到∠ABC﹣∠4＝∠ADC﹣∠3，即∠ABD＝∠CDB，得到AB∥CD，本选项符合题意；④由∠BAD+∠ABC＝180°，得到AD∥BC，本选项不合题意，
则符合题意的只有1个．
故选：C．
【点评】此题考查了平行线的判定，熟练掌握平行线的判定方法是解本题的关键．
8．已知在同一平面内，有三条直线a，b，c，若a∥b，b∥c，则直线a与直线c之间的位置关系是（　　）
A．相交 B．平行 C．垂直 D．平行或相交
【分析】根据平行公理的推论直接判断直线c与直线a的位置关系即可．
【解答】解：∵在同一平面内，直线a∥b，直线b∥c，
∴直线c与直线a的位置关系是：a∥c．
故选：B．
【点评】此题主要考查了平行公理的推论，熟练记忆推论内容是解题关键．
二．填空题（共6小题）
9．如图，直线a，b与直线c相交，给出下列条件：①∠1＝∠2；②∠3＝∠6；③∠4+∠7＝180°；④∠5+∠3＝180°，其中能判断a∥b的是　①③④　（填序号）．

【分析】直接利用平行线的判定方法分别分析得出答案．
【解答】解：①∵∠1＝∠2，
∴a∥b，故此选项正确；
②∠3＝∠6无法得出a∥b，故此选项错误；
③∵∠4+∠7＝180°，
∴a∥b，故此选项正确；
④∵∠5+∠3＝180°，
∴∠2+∠5＝180°，
∴a∥b，故此选项正确；
故答案为：①③④．
【点评】此题主要考查了平行线的判定，正确把握平行线的几种判定方法是解题关键．
10．如图把三角板的直角顶点放在直线b上，若∠1＝40°，则当∠2＝　50　度时，a∥b．

【分析】由直角三角板的性质可知∠3＝180°﹣∠1﹣90°＝50°，当∠2＝50°时，∠2＝∠3，得出a∥b即可．
【解答】解：当∠2＝50°时，a∥b；理由如下：
如图所示：
∵∠1＝40°，
∴∠3＝180°﹣90°﹣40°＝50°，
当∠2＝50°时，∠2＝∠3，
∴a∥b；
故答案为：50．

【点评】本题考查了平行线的判定方法、平角的定义；熟记同位角相等，两直线平行是解决问题的关键．
11．如图，∠C＝120°，请添加一个条件，使得AB∥CD，则符合要求的其中一个条件可以是　∠BEC＝60° （答案不唯一）　．

【分析】欲证AB∥CD，在图中发现AB、CD被一直线所截，且已知一同旁内角∠C＝120°，故可按同旁内角互补两直线平行补充条件．
【解答】解：因为∠C＝120°，
要使AB∥CD，
则要∠BEC＝180°﹣120°＝60°（同旁内角互补两直线平行）．
故答案为：∠BEC＝60° （答案不唯一）．
【点评】此题考查平行线的判定，解答此类要判定两直线平行的题，可围绕截线找同位角、内错角和同旁内角．本题是一道探索性条件开放性题目，能有效地培养“执果索图”的思维方式与能力．
12．如图：
（1）如果∠1＝∠B，那么　AB　∥　CD　，根据是　同位角相等，两直线平行　；
（2）如果∠3＝∠D，那么　BE　∥　DF　，根据是　内错角相等，两直线平行　；
（3）如果要使BE∥DF，必须∠1＝∠　D　，根据是　同位角相等，两直线平行　．

【分析】根据平行线的判定方法答题．
【解答】解：（1）如果∠1＝∠B，那么AB∥CD，根据是同位角相等，两直线平行；
（2）如果∠3＝∠D，那么BE∥DF，根据是内错角相等，两直线平行；
（3）如果要使BE∥DF，必须∠1＝∠D，根据是同位角相等，两直线平行．
【点评】正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．
13．如图所示：
（1）若∠2＝∠A，则　AB　∥　CE　，理由为　内错角相等两直线平行　；
（2）若∠B＝　∠3　，则AB∥CE，理由为　同位角相等两直线平行　；
（3）若∠B+∠BCE＝180°，则　AB　∥　CE　，理由是　同旁内角互补两直线平行　．

【分析】结合图形，利用平行线的性质及判定判断即可得到结果．
【解答】解：（1）若∠2＝∠A，则AB∥CE，理由为内错角相等，两直线平行；
（2）若∠B＝∠3，则AB∥CE，理由为同位角相等，两直线平行；
（3）若∠B+∠BCE＝180°，则AB∥CE，理由是同旁内角互补，两直线平行．
故答案为：（1）AB；CE；内错角相等，两直线平行；
（2）∠3；同位角相等，两直线平行；
（3）AB；CE；同旁内角互补，两直线平行
【点评】此题考查了平行线的判定，熟练掌握平行线的判定方法是解本题的关键．
14．观察图形．
（1）∵∠A＝∠3，∴　AC　∥　EF　，理由是　同位角相等，两直线平行　；
（2）∵∠2＝∠4，∴AC∥　EF　，理由是　内错角相等，两直线平行　；
（3）∵∠5＝　∠C　，∴EF∥　AC　，理由是　同位角相等，两直线平行　；
（4）∵∠5＝　∠4　，∴BC∥　DE　，理由是　内错角相等，两直线平行　；
（5）∵∠6+∠C＝180°，∴　EF　∥　AC　，理由是　同旁内角互补，两直线平行　；
（6）∵∠6+　∠4　＝180°，∴DE∥　BC　，理由是　同旁内角互补，两直线平行　．

【分析】分别根据平行线的判定定理：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行分别进行分析即可．
【解答】（1）∵∠A＝∠3，∴AC∥EF，理由是 同位角相等，两直线平行；

（2）∵∠2＝∠4，∴AC∥EF，理由是 内错角相等，两直线平行；

（3）∵∠5＝∠C，∴EF∥AC，理由是 同位角相等，两直线平行；

（4）∵∠5＝∠4，∴BC∥DE，理由是 内错角相等，两直线平行；

（5）∵∠6+∠C＝180°，∴EF∥AC，理由是 同旁内角互补，两直线平行；

（6）∵∠6+∠4＝180°，∴DE∥BC，理由是 同旁内角互补，两直线平行．
【点评】此题主要考查了平行线的判定，关键是掌握平行线的判定定理．
三．解答题（共6小题）
15．如图，AB∥CD，AE平分∠BAD，CD与AE相交于F，∠CFE＝∠E．求证：AD∥BC．

【分析】首先利用平行线的性质以及角平分线的性质得到满足关于AD∥BC的条件，内错角∠2和∠E相等，得出结论．
【解答】证明：∵AE平分∠BAD，
∴∠1＝∠2，
∵AB∥CD，∠CFE＝∠E，
∴∠1＝∠CFE＝∠E，
∴∠2＝∠E，
∴AD∥BC．
【点评】本题考查角平分线的性质以及平行线的判定定理．
16．如图，AD∥BC，∠EAD＝∠C，∠FEC＝∠BAE，∠EFC＝50°
（1）求证：AE∥CD；
（2）求∠B的度数．

【分析】（1）根据平行线的性质和等量关系可得∠EAD+∠D＝180°，根据同旁内角互补，两直线平行即可证明；
（2）根据平行线的性质可得∠AEB＝∠C，根据三角形内角和定理和等量关系即可得到∠B的度数．
【解答】（1）证明：∵AD∥BC，
∴∠D+∠C＝180°，
∵∠EAD＝∠C，
∴∠EAD+∠D＝180°，
∴AE∥CD；
（2）∵AE∥CD，
∴∠AEB＝∠C，
∵∠FEC＝∠BAE，
∴∠B＝∠EFC＝50°．
【点评】考查了平行线的判定和性质，三角形内角和定理，解题的关键是证明AE∥CD．
17．填写推理理由：
如图，CD∥EF，∠1＝∠2，求证：∠3＝∠ACB．
证明：∵CD∥EF，
∴∠DCB＝∠2　两直线平行，同位角相等　
∵∠1＝∠2，∴∠DCB＝∠1．　等量代换　
∴GD∥CB　内错角相等，两直线平行　．
∴∠3＝∠ACB　两直线平行，同位角相等　．

【分析】根据两直线平行，同位角相等可以求出∠DCB＝∠2，等量代换得出∠DCB＝∠1，再根据内错角相等，两直线平行得出GD∥CB，最后根据两直线平行，同位角相等，所以∠3＝∠ACB．
【解答】证明：∵CD∥EF，
∴∠DCB＝∠2（两直线平行，同位角相等），
∵∠1＝∠2，∴∠DCB＝∠1（等量代换）．
∴GD∥CB（内错角相等，两直线平行）．
∴∠3＝∠ACB（两直线平行，同位角相等）．
故答案为两直线平行，同位角相等；等量代换；内错角相等，两直线平行；两直线平行，同位角相等．
【点评】本题考查了平行线的判定与性质，熟练掌握平行线的判定方法和性质，并准确识图是解题的关键．
18．如图，BE平分∠ABD，DE平分∠BDC，且∠1+∠2＝90°．
求证：AB∥CD．

【分析】运用角平分线的定义，结合图形可知∠ABD＝2∠1，∠BDC＝2∠2，又已知∠1+∠2＝90°，可得同旁内角∠ABD和∠BDC互补，从而证得AB∥CD．
【解答】解：∵BE平分∠ABD，DE平分∠BDC（已知），
∴∠ABD＝2∠1，∠BDC＝2∠2（角平分线定义），
∵∠1+∠2＝90°，
∴∠ABD+∠BDC＝2（∠1+∠2）＝180°，
∴AB∥CD（同旁内角互补，两直线平行）．
【点评】本题考查平行线的判定和角平分线的定义．灵活运用角平分线的定义和角的和差的关系是解决本题的关键，注意正确识别“三线八角”中的同位角、内错角、同旁内角．
19．完成下面的解题过程，并在括号内填上依据．
如图，∠AHF+∠FMD＝180°，GH平分∠AHF，MN平分∠DME．
求证：GH∥MN．
证明：∵∠AHF+∠FMD＝180°，　∠DME　+∠FMD＝180°，
∴　∠AHF＝∠DME　．
∵GH平分∠AHF，MN平分∠DME，
∴∠1＝∠AHF，∠2＝∠DME　（角平分线的定义）　．
∴∠1＝∠2　（等量关系）　．
∴GH∥MN　（内错角相等，两直线平行）　．

【分析】根据邻补角的定义和等量关系可得∠AHF＝∠DME，由GH平分∠AHF，MN平分∠DME，根据角平分线定义得到∠1＝∠AHF，∠2＝∠DME，进一步得到∠1＝∠2，再根据平行线的判定方法可得GH∥MN．
【解答】证明：∵∠AHF+∠FMD＝180°，∠DME+∠FMD＝180°，
∴∠AHF＝∠DME．
∵GH平分∠AHF，MN平分∠DME，
∴∠1＝∠AHF，∠2＝∠DME （角平分线的定义）．
∴∠1＝∠2 （等量关系）．
∴GH∥MN（内错角相等，两直线平行）．
故答案为：∠DME，∠AHF＝∠DME．（角平分线的定义）．（等量关系）．（内错角相等，两直线平行）．
【点评】本题考查了平行线的判定：内错角相等，两直线平行．也考查了角平分线的定义．
20．如图，已知∠1＝60°，∠2＝60°，∠MAE＝45°，∠FEG＝15°，EG平分∠AEC，∠NCE＝75°．求证：
（1）AB∥EF．
（2）AB∥ND．

【分析】（1）求出∠1＝∠2，根据平行线的判定推出即可；
（2）求出∠AEF，求出∠AEG，根据角平分线求出∠CEG，求出∠CEF＝∠NCE＝75°，根据平行线的判定推出EF∥ND即可．
【解答】（1）证明：∵∠1＝60°，∠2＝60°，
∴∠2＝∠1，
∴AB∥EF．

（2）证明：∵AB∥EF，∠MAE＝45°，
∴∠AEF＝∠MAE＝45°，
∵∠FEG＝15°，
∴∠AEG＝45°+15°＝60°，
∵EG平分∠AEC，
∴∠CEG＝∠AEG＝60°，
∴∠FEC＝60°+15°＝75°，
∵∠NCE＝75°，
∴∠FEC＝∠NCE＝75°，
∴EF∥ND，
∵AB∥EF，
∴AB∥ND．
【点评】本题考查了角平分线和平行线的性质和判定，主要考查学生的推理能力．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布
日期：2019/1/29 9:36:23；用户：zhrasce20；邮箱：zhrasce20@163.com；学号：6322261










21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）



HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)