1.4 平行线的性质同步练习

中小学教育资源及组卷应用平台


绝密★启用前
浙教版七年级下同步练习第一章平行线
1.4 平行线的性质
题号 一 二 三 总分
得分
注意事项：
1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上
第Ⅰ卷（选择题）
请点击修改第I卷的文字说明
评卷人 得 分

一．选择题（共8小题）
1．如图，直线AB∥CD，则下列结论正确的是（　　）

A．∠1＝∠2 B．∠3＝∠4 C．∠1+∠3＝180° D．∠3+∠4＝180°
2．如图，将一张含有30°角的三角形纸片的两个顶点叠放在矩形的两条对边上，若∠2＝44°，则∠1的大小为（　　）

A．14° B．16° C．90°﹣α D．α﹣44°
3．如图，AD∥BC，∠C＝30°，∠ADB：∠BDC＝1：2，则∠DBC的度数是（　　）

A．30° B．36° C．45° D．50°
4．如图，把一个直角三角尺的直角顶点放在直尺的一边上，若∠1＝50°，则∠2＝（　　）

A．20° B．30° C．40° D．50°
5．如图，已知AD∥BC，∠B＝30°，DB平分∠ADE，则∠DEC＝（　　）

A．30° B．60° C．90° D．120°
6．如图所示，直线a∥b，∠1＝35°，∠2＝90°，则∠3的度数为（　　）

A．125° B．135° C．145° D．155°
7．如图，∠B＝∠C，∠A＝∠D，下列结论：①AB∥CD；②AE∥DF；③AE⊥BC；④∠AMC＝∠BND，其中正确的结论有（　　）

A．①②④ B．②③④ C．③④ D．①②③④
8．如图所示，AB∥CD，则∠A+∠E+∠F+∠C等于（　　）

A．180° B．360° C．540° D．720°



第Ⅱ卷（非选择题）
请点击修改第Ⅱ卷的文字说明
评卷人 得 分

二．填空题（共6小题）
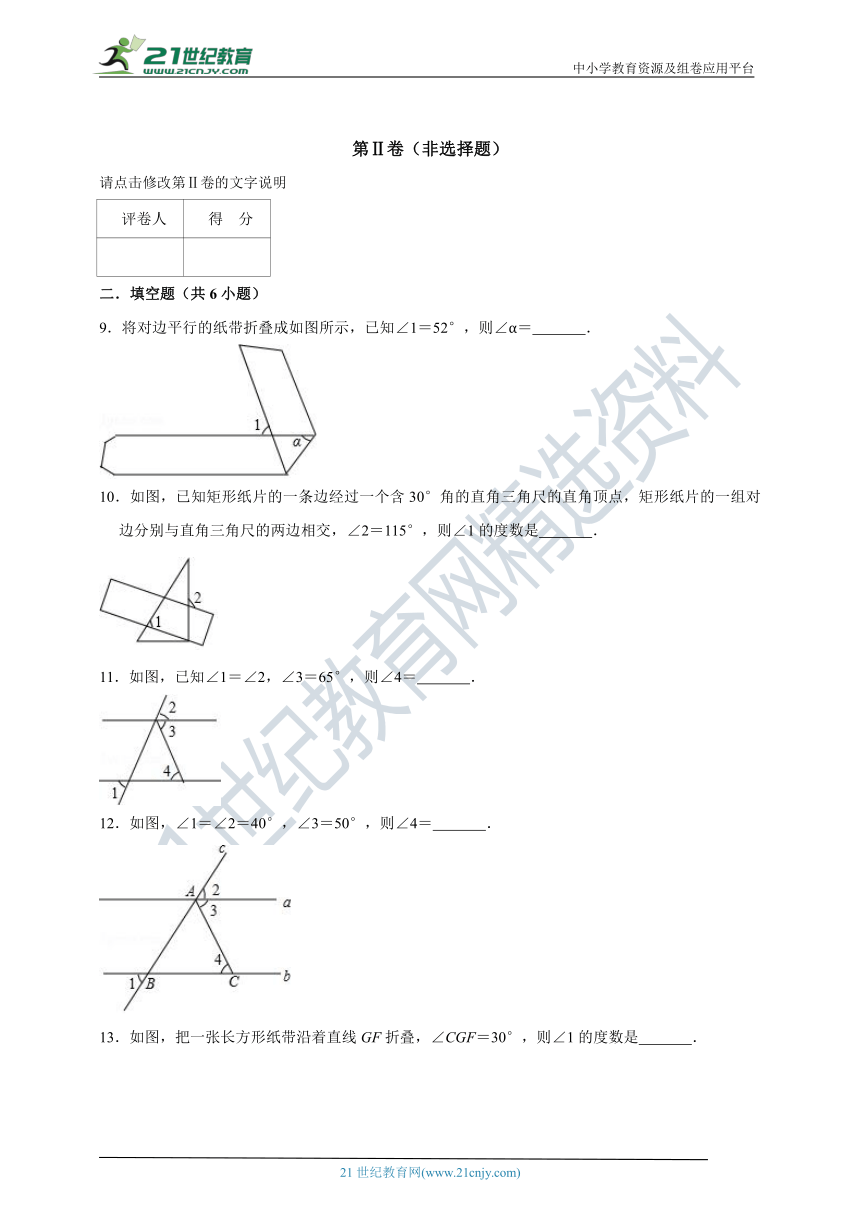
9．将对边平行的纸带折叠成如图所示，已知∠1＝52°，则∠α＝　 　．

10．如图，已知矩形纸片的一条边经过一个含30°角的直角三角尺的直角顶点，矩形纸片的一组对边分别与直角三角尺的两边相交，∠2＝115°，则∠1的度数是　 　．

11．如图，已知∠1＝∠2，∠3＝65°，则∠4＝　 　．

12．如图，∠1＝∠2＝40°，∠3＝50°，则∠4＝　 　．

13．如图，把一张长方形纸带沿着直线GF折叠，∠CGF＝30°，则∠1的度数是　 　．

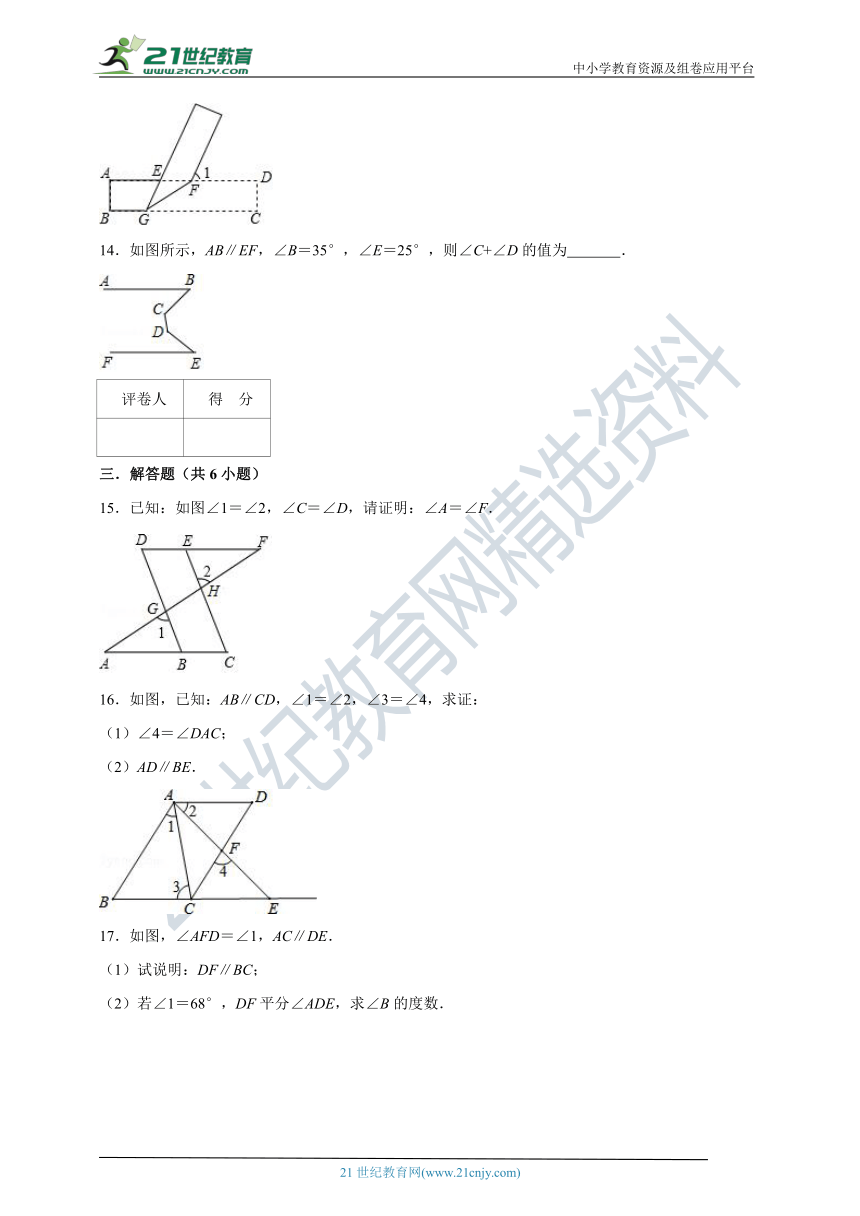
14．如图所示，AB∥EF，∠B＝35°，∠E＝25°，则∠C+∠D的值为　 　．

评卷人 得 分

三．解答题（共6小题）
15．已知：如图∠1＝∠2，∠C＝∠D，请证明：∠A＝∠F．

16．如图，已知：AB∥CD，∠1＝∠2，∠3＝∠4，求证：
（1）∠4＝∠DAC；
（2）AD∥BE．

17．如图，∠AFD＝∠1，AC∥DE．
（1）试说明：DF∥BC；
（2）若∠1＝68°，DF平分∠ADE，求∠B的度数．

18．如图①，已知AD∥BC，∠B＝∠D＝120°．
（1）请问：AB与CD平行吗？为什么？
（2）若点E、F在线段CD上，且满足AC平分∠BAE，AF平分∠DAE，如图②，求∠FAC的度数．
（3）若点E在直线CD上，且满足∠EAC＝∠BAC，求∠ACD：∠AED的值（请自己画出正确图形，并解答）．

19．已知AB∥CD，解决下列问题：
（1）如图①，BP、DP分别平分∠ABE、∠CDE，若∠E＝100°，求∠P的度数．
（2）如图②，若∠ABP＝∠ABE，∠CDP＝∠CDE，试写出∠P与∠E的数量关系并说明理由．
（3）如图③，若∠ABP＝∠ABE，∠CDP＝∠CDE，设∠E＝m°，求∠P的度数（直接用含n、m的代数式表示，不需说明理由）．

20．问题情境：如图1，AB∥CD，∠PAB＝130°，∠PCD＝120°，求∠APC的度数．
小明的思路是过点P作PE∥AB，通过平行线的性质来求∠APC．
（1）按照小明的思路，求∠APC的度数；
（2）问题迁移：如图2，AB∥CD，点P在射线ON上运动，记∠PAB＝α，∠PCD＝β，当点P在B、D两点之间运动时，问∠APC与α、β之间有何数量关系？请说明理由；
（3）在（2）的条件下，如果点P不在B、D两点之间运动时（点P与点O、B、D三点不重合），请直接写出∠APC与α、β之间的数量关系．




参考答案与试题解析
一．选择题（共8小题）
1．如图，直线AB∥CD，则下列结论正确的是（　　）

A．∠1＝∠2 B．∠3＝∠4 C．∠1+∠3＝180° D．∠3+∠4＝180°
【分析】依据AB∥CD，可得∠3+∠5＝180°，再根据∠5＝∠4，即可得出∠3+∠4＝180°．
【解答】解：如图，∵AB∥CD，
∴∠3+∠5＝180°，
又∵∠5＝∠4，
∴∠3+∠4＝180°，
故选：D．

【点评】本题考查了平行线的性质，解题时注意：两直线平行，同旁内角互补．
2．如图，将一张含有30°角的三角形纸片的两个顶点叠放在矩形的两条对边上，若∠2＝44°，则∠1的大小为（　　）

A．14° B．16° C．90°﹣α D．α﹣44°
【分析】依据平行线的性质，即可得到∠2＝∠3＝44°，再根据三角形外角性质，可得∠3＝∠1+30°，进而得出∠1＝44°﹣30°＝14°．
【解答】解：如图，∵矩形的对边平行，
∴∠2＝∠3＝44°，
根据三角形外角性质，可得∠3＝∠1+30°，
∴∠1＝44°﹣30°＝14°，
故选：A．

【点评】本题主要考查了平行线的性质以及三角形外角性质的运用，解题时注意：两直线平行，同位角相等．
3．如图，AD∥BC，∠C＝30°，∠ADB：∠BDC＝1：2，则∠DBC的度数是（　　）

A．30° B．36° C．45° D．50°
【分析】直接利用平行线的性质得出∠ADC＝150°，∠ADB＝∠DBC，进而得出∠ADB的度数，即可得出答案．
【解答】解：∵AD∥BC，∠C＝30°，
∴∠ADC＝150°，∠ADB＝∠DBC，
∵∠ADB：∠BDC＝1：2，
∴∠ADB＝×150°＝50°，
∴∠DBC的度数是50°．
故选：D．
【点评】此题主要考查了平行线的性质，正确得出∠ADB度数是解题关键．
4．如图，把一个直角三角尺的直角顶点放在直尺的一边上，若∠1＝50°，则∠2＝（　　）

A．20° B．30° C．40° D．50°
【分析】根据两直线平行，同位角相等可得∠3＝∠1，再根据平角等于180°列式计算即可得解．
【解答】解：∵直尺对边互相平行，
∴∠3＝∠1＝50°，
∴∠2＝180°﹣50°﹣90°＝40°．
故选：C．

【点评】本题考查了平行线的性质，平角的定义，熟记性质并准确识图是解题的关键．
5．如图，已知AD∥BC，∠B＝30°，DB平分∠ADE，则∠DEC＝（　　）

A．30° B．60° C．90° D．120°
【分析】根据平行线的性质：两条直线平行，内错角相等及角平分线的性质，三角形内角和定理解答．
【解答】解：∵AD∥BC，
∴∠ADB＝∠B＝30°，
再根据角平分线的概念，得：∠BDE＝∠ADB＝30°，
再根据两条直线平行，内错角相等得：∠DEC＝∠ADE＝60°，
故选：B．
【点评】考查了平行线的性质、角平分线的概念，要熟练掌握．
6．如图所示，直线a∥b，∠1＝35°，∠2＝90°，则∠3的度数为（　　）

A．125° B．135° C．145° D．155°
【分析】如图求出∠5即可解决问题．
【解答】解：

∵a∥b，
∴∠1＝∠4＝35°，
∵∠2＝90°，
∴∠4+∠5＝90°，
∴∠5＝55°，
∴∠3＝180°﹣∠5＝125°，
故选：A．
【点评】本题考查平行线的性质、三角形内角和定理，邻补角的性质等知识，解题的关键是灵活运用所学知识解决问题．
7．如图，∠B＝∠C，∠A＝∠D，下列结论：①AB∥CD；②AE∥DF；③AE⊥BC；④∠AMC＝∠BND，其中正确的结论有（　　）

A．①②④ B．②③④ C．③④ D．①②③④
【分析】由条件可先证明AB∥CD，再证明AE∥DF，结合平行线的性质及对顶角相等可得到∠AMC＝∠BND，可得出答案．
【解答】解：∵∠B＝∠C，
∴AB∥CD，
∴∠A＝∠AEC，
又∵∠A＝∠D，
∴∠AEC＝∠D，
∴AE∥DF，
∴∠AMC＝∠FNM，
又∵∠BND＝∠FNM，
∴∠AMC＝∠BND，
故①②④正确，
由条件不能得出∠AMC＝90°，故③不一定正确；
故选：A．
【点评】本题主要考查平行线的性质和判定，掌握平行线的性质和判定是解题的关键，即①两直线平行?同位角相等，②两直线平行?内错角相等，③两直线平行?同旁内角互补，④a∥b，b∥c?a∥c．
8．如图所示，AB∥CD，则∠A+∠E+∠F+∠C等于（　　）

A．180° B．360° C．540° D．720°
【分析】分别过E、F作AB或CD的平行线，运用平行线的性质求解．
【解答】解：作EM∥AB，FN∥AB，
∵AB∥CD，∴AB∥EM∥FN∥CD．
∴∠A+∠AEM＝180°，∠MEF+∠EFN＝180°，∠NFC+∠C＝180°，
∴∠A+∠AEF+∠EFC+∠C＝540°．
故选：C．

【点评】注意此类题要常作的辅助线，充分运用平行线的性质探求角之间的关系．
二．填空题（共6小题）
9．将对边平行的纸带折叠成如图所示，已知∠1＝52°，则∠α＝　64°　．

【分析】依据∠α＝∠3，以及∠1＝∠4＝52°，即可得到∠α＝（180°﹣52°）＝64°．
【解答】解：∵对边平行，
∴∠2＝∠α，
由折叠可得，∠2＝∠3，
∴∠α＝∠3，
又∵∠1＝∠4＝52°，
∴∠α＝（180°﹣52°）＝64°，
故答案为：64°．

【点评】本题主要考查了平行线的性质，解题时注意：两直线平行，内错角相等．
10．如图，已知矩形纸片的一条边经过一个含30°角的直角三角尺的直角顶点，矩形纸片的一组对边分别与直角三角尺的两边相交，∠2＝115°，则∠1的度数是　85°　．

【分析】先根据平行线的性质，得出∠3的度数，再根据三角形外角性质进行计算即可．
【解答】解：如图所示，∵DE∥BC，
∴∠2＝∠3＝115°，
又∵∠3是△ABC的外角，
∴∠1＝∠3﹣∠A＝115°﹣30°＝85°，
故答案为：85°．

【点评】本题主要考查了平行线的性质以及三角形外角性质的运用，解题时注意：两直线平行，同位角相等．
11．如图，已知∠1＝∠2，∠3＝65°，则∠4＝　65°　．

【分析】先根据平行线的判定，得出AB∥CD，再根据平行线的性质，得出∠3＝∠4，进而得到∠4的度数．
【解答】解：∵∠1＝∠2，
∴∠5＝∠6，
∴AB∥CD，
∴∠3＝∠4，
又∵∠3＝65°，
∴∠4＝65°．
故答案为：65°．

【点评】本题主要考查了平行的性质与判定，解题时注意：平行线的判定是由角的数量关系判断两直线的位置关系，平行线的性质是由平行关系来寻找角的数量关系．
12．如图，∠1＝∠2＝40°，∠3＝50°，则∠4＝　50°　．

【分析】根据对顶角相等和平行线的判定和性质解答即可．
【解答】解：∵∠ABC＝∠1，
∵∠1＝∠2＝40°，
∴∠2＝∠ABC＝40°，
∴a∥b，
∴∠3＝∠4＝50°，
故答案为：50°
【点评】此题考查平行线的判定和性质，关键是根据对顶角相等和平行线的判定和性质解答．
13．如图，把一张长方形纸带沿着直线GF折叠，∠CGF＝30°，则∠1的度数是　60°　．

【分析】根据平行线的性质可得∠CGF＝∠GFE＝30°再根据折叠可得：∠EGF＝∠FGC＝30°，再利用平行线的性质进而得到答案．
【解答】解：∵把一张长方形纸带沿着直线GF折叠，∠CGF＝30°，
∴∠EGF＝∠FGC＝30°，
∵AD∥BC，
∴∠CGF＝∠GFE＝30°，
∴∠2＝60°，
∵GE∥FH，
∴∠1＝∠2＝60°，
故答案为：60°
【点评】此题主要考查了平行线的性质，关键是掌握两直线平行内错角相等．
14．如图所示，AB∥EF，∠B＝35°，∠E＝25°，则∠C+∠D的值为　240°　．

【分析】过C作CG∥AB，过D作DH∥EF，依据AB∥EF，可得AB∥EF∥CG∥DH，进而得出∠1＝∠B＝35°，∠2＝∠E＝25°，∠GCD+∠HDC＝180°，可得∠BCD+∠CDE＝35°+180°+25°＝240°．
【解答】解：如图所示，过C作CG∥AB，过D作DH∥EF，
∵AB∥EF，
∴AB∥EF∥CG∥DH，
∴∠1＝∠B＝35°，∠2＝∠E＝25°，∠GCD+∠HDC＝180°，
∴∠BCD+∠CDE＝35°+180°+25°＝240°，
故答案为：240°．

【点评】本题主要考查了平行线的性质，解题时注意运用：两直线平行，同旁内角互补；两直线平行，内错角相等．
三．解答题（共6小题）
15．已知：如图∠1＝∠2，∠C＝∠D，请证明：∠A＝∠F．

【分析】由∠1＝∠2，∠1＝∠DGH，根据同位角相等，两直线平行，易证得DB∥EC，又由∠C＝∠D，易证得AC∥DF，继而证得结论．
【解答】证明：∵∠1＝∠2（已知），
又∵∠1＝∠DGH（对顶角相等），
∴∠2＝∠DGH（等量代换）．
∴DB∥EC（同位角相等，两直线平行）．
∴∠ABD＝∠C（两直线平行，同位角相等）
∵∠C＝∠D（已知）
∴∠ABD＝∠D（等量代换）
∴AC∥DF （内错角相等，两直线平行）
∴∠A＝∠F（两直线平行，内错角相等）．
【点评】本题考查平行线的性质与判定，解题的关键是灵活运用平行线的性质与判定，本题属于基础题型．
16．如图，已知：AB∥CD，∠1＝∠2，∠3＝∠4，求证：
（1）∠4＝∠DAC；
（2）AD∥BE．

【分析】根据平行线的性质求出∠4＝∠BAF＝∠3，求出∠DAC＝∠BAF，推出∠3＝∠BAF，根据平行线的判定推出即可．
【解答】证明：（1）：∵AB∥CD，
∴∠4＝∠BAF（两直线平行，同位角相等），
∵∠3＝∠4，
∴∠3＝∠BAF，
∵∠1＝∠2（已知）
∴∠1+∠CAF＝∠2+∠CAF（等式的性质）
即∠BAF＝∠DAC，
∴∠4＝∠DAC，
（2）∵∠4＝∠DAC，∠3＝∠4，
∴∠3＝∠DAC，
∴AD∥BE（内错角相等，两直线平行）．
【点评】本题考查了平行线的性质和判定的应用，注意：平行线的性质是：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，反之亦然．
17．如图，∠AFD＝∠1，AC∥DE．
（1）试说明：DF∥BC；
（2）若∠1＝68°，DF平分∠ADE，求∠B的度数．

【分析】（1）根据平行线的判定得出即可．
（2）根据平行线的性质求出∠B．
【解答】解：（1）∵AC∥DE，
∴∠C＝∠1，
∵∠AFD＝∠1，
∴∠C＝∠AFD，
∴DF∥BC．
（2）∵∠1＝68°，DF∥BC，
∴∠EDF＝∠1＝68°，
∵DF平分∠ADE，
∴∠ADF＝∠EDF＝68°，
∵DF∥BC，
∴∠B＝∠ADF＝68°．
【点评】本题考查了平行线的性质和判定，平行线的性质和判定是解此题的关键．
18．如图①，已知AD∥BC，∠B＝∠D＝120°．
（1）请问：AB与CD平行吗？为什么？
（2）若点E、F在线段CD上，且满足AC平分∠BAE，AF平分∠DAE，如图②，求∠FAC的度数．
（3）若点E在直线CD上，且满足∠EAC＝∠BAC，求∠ACD：∠AED的值（请自己画出正确图形，并解答）．

【分析】（1）依据平行线的性质以及判定，即可得到AB∥CD；
（2）依据AC平分∠BAE，AF平分∠DAE，即可得到∠EAC＝∠BAE，∠EAF＝∠DAE，进而得出∠FAC＝∠EAC+∠EAF＝（∠BAE+∠DAE）＝∠DAB；
（3）分两种情况讨论：当点E在线段CD上时；当点E在DC的延长线上时，分别依据AB∥CD，进而得到∠ACD：∠AED的值．
【解答】解：（1）平行．
如图①，∵AD∥BC，
∴∠A+∠B＝180°，
又∵∠B＝∠D＝120°，
∴∠D+∠A＝180°，
∴AB∥CD；

（2）如图②，∵AD∥BC，∠B＝∠D＝120°，
∴∠DAB＝60°，
∵AC平分∠BAE，AF平分∠DAE，
∴∠EAC＝∠BAE，∠EAF＝∠DAE，
∴∠FAC＝∠EAC+∠EAF＝（∠BAE+∠DAE）＝∠DAB＝30°；

（3）①如图3，当点E在线段CD上时，
由（1）可得AB∥CD，
∴∠ACD＝∠BAC，∠AED＝∠BAE，
又∵∠EAC＝∠BAC，
∴∠ACD：∠AED＝2：3；
②如图4，当点E在DC的延长线上时，
由（1）可得AB∥CD，
∴∠ACD＝∠BAC，∠AED＝∠BAE，
又∵∠EAC＝∠BAC，
∴∠ACD：∠AED＝2：1．


【点评】本题主要考查了平行线的性质以及判定，平行线的判定是由角的数量关系判断两直线的位置关系，平行线的性质是由平行关系来寻找角的数量关系．
19．已知AB∥CD，解决下列问题：
（1）如图①，BP、DP分别平分∠ABE、∠CDE，若∠E＝100°，求∠P的度数．
（2）如图②，若∠ABP＝∠ABE，∠CDP＝∠CDE，试写出∠P与∠E的数量关系并说明理由．
（3）如图③，若∠ABP＝∠ABE，∠CDP＝∠CDE，设∠E＝m°，求∠P的度数（直接用含n、m的代数式表示，不需说明理由）．

【分析】（1）过E作EF∥AB，依据平行线的性质，即可得到∠ABE+∠BED+∠CDE＝360°，再根据∠BED＝100°，BP、DP分别平分∠ABE、∠CDE，即可得到∠P的度数．
（2）过E作EF∥AB，依据平行线的性质，即可得到∠ABE+∠CDE＝360°﹣∠BED，再根据∠ABP＝∠ABE，∠CDP＝∠CDE，即可得到∠PBE+∠PDE＝（∠ABE+∠CDE）＝240°﹣∠BED，再根据四边形内角和得出∠P与∠E的数量关系；
（3）利用平行线的性质可得∠ABE+∠CDE＝360°﹣∠BED＝360°﹣m°，再根据∠ABP＝∠ABE，∠CDP＝∠CDE，即可得到∠PBE+∠PDE＝（∠ABE+∠CDE）＝（360°﹣m°），再根据四边形PDEB内角和，即可得到∠P＝360°﹣（360°﹣m°）﹣m°＝．
【解答】解：（1）如图①，过E作EF∥AB，
∵AB∥CD，
∴EF∥AB∥CD，
∴∠ABE+∠BEF＝180°，∠CDE+∠DEF＝180°，
∴∠ABE+∠BED+∠CDE＝360°，
又∵∠BED＝100°，
∴∠ABE+∠CDE＝360°﹣100°＝260°，
又∵BP、DP分别平分∠ABE、∠CDE，
∴∠PBE+∠PDE＝（∠ABE+∠CDE）＝×260°＝130°，
∴∠P＝360°﹣130°﹣100°＝130°；

（2）3∠P+∠BED＝360°；
如图②，过E作EF∥AB，
∵AB∥CD，
∴EF∥AB∥CD，
∴∠ABE+∠BEF＝180°，∠CDE+∠DEF＝180°，
∴∠ABE+∠BED+∠CDE＝360°，
∴∠ABE+∠CDE＝360°﹣∠BED，
又∵∠ABP＝∠ABE，∠CDP＝∠CDE，
∴∠PBE+∠PDE＝（∠ABE+∠CDE）＝×（360°﹣∠BED）＝240°﹣∠BED，
∴∠P＝360°﹣∠BED﹣（240°﹣∠BED）＝120°﹣∠BED，
即3∠P+∠BED＝360°；

（3）∠P＝．
如图③，过E作EF∥AB，
∵AB∥CD，
∴EF∥AB∥CD，
同理可得，∠ABE+∠CDE＝360°﹣∠BED＝360°﹣m°，
又∵∠ABP＝∠ABE，∠CDP＝∠CDE，
∴∠PBE+∠PDE＝（∠ABE+∠CDE）＝（360°﹣m°），
∴四边形PDEB中，∠P＝360°﹣（360°﹣m°）﹣m°＝．



【点评】此题主要考查了平行线的性质和应用，解答此题的关键是要明确：两条平行线被第三条直线所截，同旁内角互补．简单说成：两直线平行，同旁内角互补．
20．问题情境：如图1，AB∥CD，∠PAB＝130°，∠PCD＝120°，求∠APC的度数．
小明的思路是过点P作PE∥AB，通过平行线的性质来求∠APC．
（1）按照小明的思路，求∠APC的度数；
（2）问题迁移：如图2，AB∥CD，点P在射线ON上运动，记∠PAB＝α，∠PCD＝β，当点P在B、D两点之间运动时，问∠APC与α、β之间有何数量关系？请说明理由；
（3）在（2）的条件下，如果点P不在B、D两点之间运动时（点P与点O、B、D三点不重合），请直接写出∠APC与α、β之间的数量关系．

【分析】（1）过P作PE∥AB，通过平行线性质可得∠A+∠APE＝180°，∠C+∠CPE＝180°再代入∠PAB＝130°，∠PCD＝120°可求∠APC即可；
（2）过P作PE∥AD交AC于E，推出AB∥PE∥DC，根据平行线的性质得出∠α＝∠APE，∠β＝∠CPE，即可得出答案；
（3）分两种情况：P在BD延长线上；P在DB延长线上，分别画出图形，根据平行线的性质得出∠α＝∠APE，∠β＝∠CPE，即可得出答案．
【解答】（1）解：过点P作PE∥AB，
∵AB∥CD，
∴PE∥AB∥CD，
∴∠A+∠APE＝180°，∠C+∠CPE＝180°，
∵∠PAB＝130°，∠PCD＝120°，
∴∠APE＝50°，∠CPE＝60°，
∴∠APC＝∠APE+∠CPE＝110°．

（2）∠APC＝∠α+∠β，
理由：如图2，过P作PE∥AB交AC于E，

∵AB∥CD，
∴AB∥PE∥CD，
∴∠α＝∠APE，∠β＝∠CPE，
∴∠APC＝∠APE+∠CPE＝∠α+∠β；

（3）如图所示，当P在BD延长线上时，
∠CPA＝∠α﹣∠β；

如图所示，当P在DB延长线上时，
∠CPA＝∠β﹣∠α．

【点评】本题主要考查了平行线的性质和判定的应用，主要考查学生的推理能力，题目是一道比较典型的题目，解题时注意分类思想的运用．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布
日期：2019/1/30 5:19:19；用户：zhrasce20；邮箱：zhrasce20@163.com；学号：6322261








































21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）



HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)