3.3 多项式的乘法同步练习

中小学教育资源及组卷应用平台


绝密★启用前
浙教版七下同步练习第三章整式的乘除
3.3 多项式的乘法
题号 一 二 三 总分
得分
注意事项：
1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上
第Ⅰ卷（选择题）
请点击修改第I卷的文字说明
评卷人 得 分

一．选择题（共8小题）
1．下列运算正确的是（　　）
A．（﹣2a）3＝﹣6a3 B．﹣3a2?4a3＝﹣12a5
C．﹣3a（2﹣a）＝6a﹣3a2 D．2a3﹣a2＝2a
2．若x﹣y+3＝0，则x（x﹣4y）+y（2x+y）的值为（　　）
A．9 B．﹣9 C．3 D．﹣3
3．已知a2+a﹣3＝0，那么a2（a+4）的值是（　　）
A．﹣18 B．﹣12
C．9 D．以上答案都不对
4．计算（a﹣2）（a+3）的结果是（　　）
A．a2﹣6 B．a2+a﹣6 C．a2+6 D．a2﹣a+6
5．已知a+b＝4，ab＝3，则代数式（a+2）（b+2）的值是（　　）
A．7 B．9 C．11 D．15
6．使（x2+px+8）（x2﹣3x+q）乘积中不含x2与x3项的p、q的值是（　　）
A．p＝0，q＝0 B．p＝3，q＝1 C．p＝﹣3，q＝﹣9 D．p＝﹣3，q＝1
7．若（x﹣5）（2x﹣n）＝2x2+mx﹣15，则m、n的值分别是（　　）
A．m＝﹣7，n＝3 B．m＝7，n＝﹣3 C．m＝﹣7，n＝﹣3 D．m＝7，n＝3
8．通过计算几何图形的面积可表示一些代数恒等式，右图可表示的代数恒等式是（　　）

A．（a﹣b）2＝a2﹣2ab+b2 B．2a（a+b）＝2a2+2ab
C．（a+b）2＝a2+2ab+b2 D．（a+b）（a﹣b）＝a2﹣b2



第Ⅱ卷（非选择题）
请点击修改第Ⅱ卷的文字说明
评卷人 得 分

二．填空题（共6小题）
9．已知一个多项式与﹣2xy的乘积为﹣6x2y2+8xy2﹣2xy，则这个多项式为　 　．
10．填空：
（1）（﹣3x2）（﹣x2+2x﹣1）＝　 　；
（2）﹣（2x﹣4x3﹣8）?（﹣x2）＝　 　；
（3）2（a2b2﹣ab+1）+3ab（1﹣ab）＝　 　；
（4）（﹣3x2）（x2﹣2x﹣3）+3x（x3﹣2x2﹣5）＝　 　；
（5）8m（m2﹣3m+4）﹣m2（m﹣3）＝　 　；
（6）7x（2x﹣1）﹣3x（4x﹣1）﹣2x（x+3）+1＝　 　；
（7）（﹣2a2b）2（ab2﹣a2b+a3）＝　 　；
（8）﹣（﹣x）2?（﹣2x2y）3+2x2（x6y3﹣1）＝　 　．
11．若M＝（x﹣2）（x﹣8），N＝（x﹣3）（x﹣7），则M﹣N＝　 　．
12．若a的值使得x2+4x+a＝（x﹣5）（x+9）﹣2成立，则a的值为　 　．
13．如图，正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼一个长为（a+3b），宽为（2a+b）的长方形，则需要C类卡片　 　张．

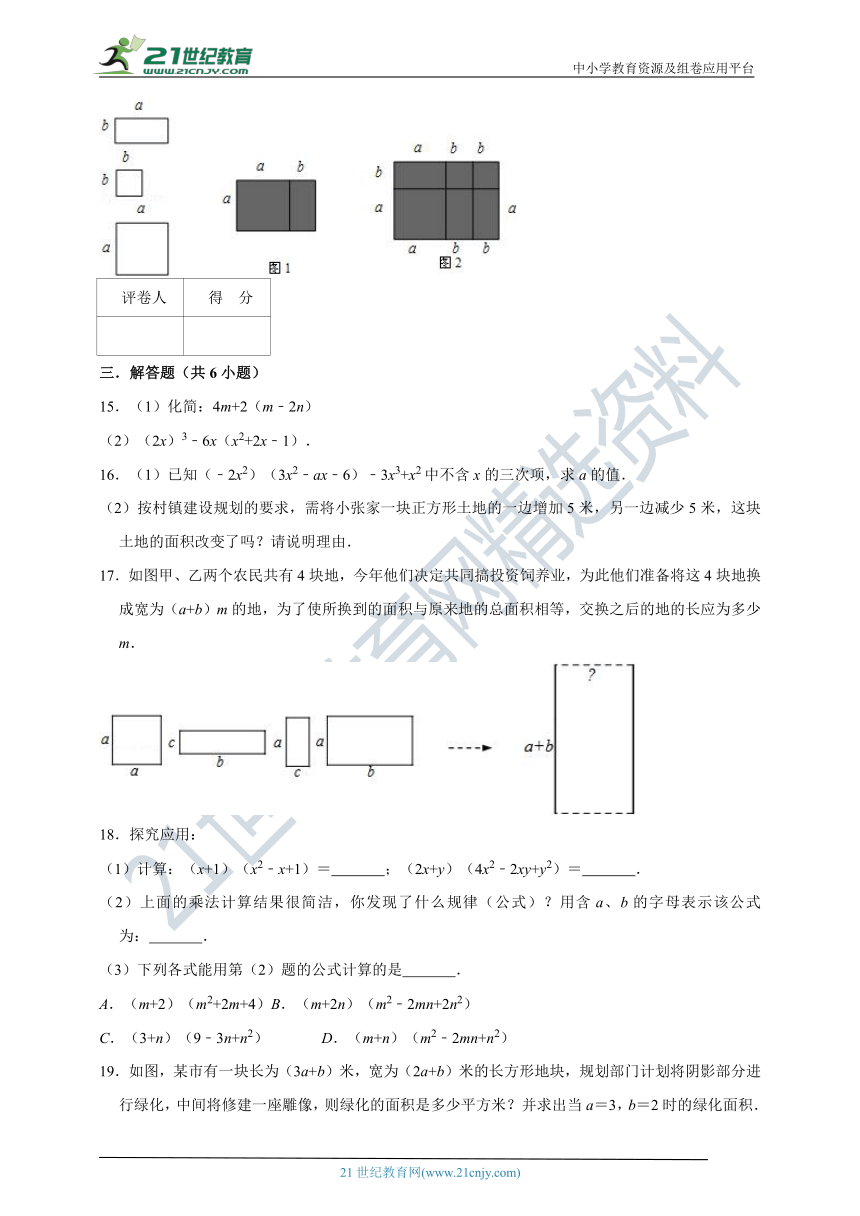
14．如图，有多个长方形和正方形的卡片，图甲是选取了2块不同的卡片，拼成的一个图形，借助图中阴影部分面积的不同表示可以用来验证等式a（a+b）＝a2+ab成立，根据图乙，利用面积的不同表示方法，仿照上边的式子写出一个等式　 　．

评卷人 得 分

三．解答题（共6小题）
15．（1）化简：4m+2（m﹣2n）
（2）（2x）3﹣6x（x2+2x﹣1）．
16．（1）已知（﹣2x2）（3x2﹣ax﹣6）﹣3x3+x2中不含x的三次项，求a的值．
（2）按村镇建设规划的要求，需将小张家一块正方形土地的一边增加5米，另一边减少5米，这块土地的面积改变了吗？请说明理由．
17．如图甲、乙两个农民共有4块地，今年他们决定共同搞投资饲养业，为此他们准备将这4块地换成宽为（a+b）m的地，为了使所换到的面积与原来地的总面积相等，交换之后的地的长应为多少m．

18．探究应用：
（1）计算：（x+1）（x2﹣x+1）＝　 　；（2x+y）（4x2﹣2xy+y2）＝　 　．
（2）上面的乘法计算结果很简洁，你发现了什么规律（公式）？用含a、b的字母表示该公式为：　 　．
（3）下列各式能用第（2）题的公式计算的是　 　．
A．（m+2）（m2+2m+4）B．（m+2n）（m2﹣2mn+2n2）
C．（3+n）（9﹣3n+n2） D．（m+n）（m2﹣2mn+n2）
19．如图，某市有一块长为（3a+b）米，宽为（2a+b）米的长方形地块，规划部门计划将阴影部分进行绿化，中间将修建一座雕像，则绿化的面积是多少平方米？并求出当a＝3，b＝2时的绿化面积．

20．欢欢与乐乐两人共同计算（2x+a）（3x+b），欢欢抄错为（2x﹣a）（3x+b），得到的结果为6x2﹣13x+6；乐乐抄错为（2x+a）（x+b），得到的结果为2x2﹣x﹣6．
（1）式子中的a、b的值各是多少？
（2）请计算出原题的正确答案．



参考答案与试题解析
一．选择题（共8小题）
1．下列运算正确的是（　　）
A．（﹣2a）3＝﹣6a3 B．﹣3a2?4a3＝﹣12a5
C．﹣3a（2﹣a）＝6a﹣3a2 D．2a3﹣a2＝2a
【分析】先根据同底数幂的乘法法则，幂的乘方，积的乘方，合并同类项分别求出每个式子的值，再判断即可．
【解答】解：A、（﹣2a）3＝﹣8a3；故本选项错误；
B、﹣3a2?4a3＝﹣12a5；故本选项正确；
C、﹣3a（2﹣a）＝6+﹣3a2；故本选项错误；
D、不是同类项不能合并；故本选项错误；
故选：B．
【点评】本题考查了同底数幂的乘法法则，幂的乘方，积的乘方，合并同类项，考查学生的计算能力．
2．若x﹣y+3＝0，则x（x﹣4y）+y（2x+y）的值为（　　）
A．9 B．﹣9 C．3 D．﹣3
【分析】由于x﹣y+3＝0，可得x﹣y＝﹣3，根据单项式乘多项式、合并同类项和完全平方公式的运算法则将x（x﹣4y）+y（2x+y）变形为（x﹣y）2，再整体代入即可求解．
【解答】解：∵x﹣y+3＝0，
∴x﹣y＝﹣3，
∴x（x﹣4y）+y（2x+y）
＝x2﹣4xy+2xy+y2
＝x2﹣2xy+y2
＝（x﹣y）2
＝（﹣3）2
＝9．
故选：A．
【点评】考查了单项式乘多项式，单项式与多项式相乘时，应注意以下几个问题：①单项式与多项式相乘实质上是转化为单项式乘以单项式；②用单项式去乘多项式中的每一项时，不能漏乘；③注意确定积的符号．注意整体思想的运用．
3．已知a2+a﹣3＝0，那么a2（a+4）的值是（　　）
A．﹣18 B．﹣12
C．9 D．以上答案都不对
【分析】已知a2+a﹣3＝0则a2+a＝3，然后把所求的式子利用a2+a表示出来即可代入求解．
【解答】解：∵a2+a﹣3＝0，
∴a2+a＝3．
a2（a+4）＝a3+4a2＝a3+a2+3a2
＝a（a2+a）+3a2
＝3a+3a2
＝3（a2+a）
＝3×3
＝9．
故选：C．
【点评】本题考查了整式的化简求值，正确利用a2+a表示出所求的式子是关键．
4．计算（a﹣2）（a+3）的结果是（　　）
A．a2﹣6 B．a2+a﹣6 C．a2+6 D．a2﹣a+6
【分析】根据多项式的乘法解答即可．
【解答】解：（a﹣2）（a+3）＝a2+a﹣6，
故选：B．
【点评】此题考查多项式的乘法，关键是根据多项式乘法的法则解答．
5．已知a+b＝4，ab＝3，则代数式（a+2）（b+2）的值是（　　）
A．7 B．9 C．11 D．15
【分析】先将原式利用多项式乘以多项式法则变形，再将a+b、ab的值代入计算可得．
【解答】解：（a+2）（b+2）
＝ab+2a+2b+4
＝ab+2（a+b）+4
当a+b＝4、ab＝3时，
原式＝3+2×4+4
＝3+8+4
＝15，
故选：D．
【点评】本题主要考查代数式的求值，解题的关键是掌握多项式乘多项式的法则及整体代入思想的运用．
6．使（x2+px+8）（x2﹣3x+q）乘积中不含x2与x3项的p、q的值是（　　）
A．p＝0，q＝0 B．p＝3，q＝1 C．p＝﹣3，q＝﹣9 D．p＝﹣3，q＝1
【分析】把式子展开，找到所有x2和x3项的系数，令它们的系数分别为0，列式求解即可．
【解答】解：∵（x2+px+8）（x2﹣3x+q），
＝x4﹣3x3+qx2+px3﹣3px2+pqx+8x2﹣24x+8q，
＝x4+（p﹣3）x3+（q﹣3p+8）x2+（pq﹣24）x+8q．
∵乘积中不含x2与x3项，
∴p﹣3＝0，q﹣3p+8＝0，
∴p＝3，q＝1．
故选：B．
【点评】灵活掌握多项式乘以多项式的法则，注意各项符号的处理．
7．若（x﹣5）（2x﹣n）＝2x2+mx﹣15，则m、n的值分别是（　　）
A．m＝﹣7，n＝3 B．m＝7，n＝﹣3 C．m＝﹣7，n＝﹣3 D．m＝7，n＝3
【分析】直接利用多项式乘以多项式运算法则去括号，进而得出关于m，n的等式求出答案．
【解答】解：∵（x﹣5）（2x﹣n）＝2x2+mx﹣15，
∴2x2﹣（10+n）x+5n＝2x2+mx﹣15，
故，
解得：．
故选：C．
【点评】此题主要考查了多项式乘以多项式，正确掌握多项式乘法运算法则是解题关键．
8．通过计算几何图形的面积可表示一些代数恒等式，右图可表示的代数恒等式是（　　）

A．（a﹣b）2＝a2﹣2ab+b2 B．2a（a+b）＝2a2+2ab
C．（a+b）2＝a2+2ab+b2 D．（a+b）（a﹣b）＝a2﹣b2
【分析】由题意知，长方形的面积等于长2a乘以宽（a+b），面积也等于四个小图形的面积之和，从而建立两种算法的等量关系．
【解答】解：长方形的面积等于：2a（a+b），
也等于四个小图形的面积之和：a2+a2+ab+ab＝2a2+2ab，
即2a（a+b）＝2a2+2ab．
故选：B．
【点评】本题考查了单项式乘多项式的几何解释，列出面积的两种不同表示方法是解题的关键．
二．填空题（共6小题）
9．已知一个多项式与﹣2xy的乘积为﹣6x2y2+8xy2﹣2xy，则这个多项式为　3xy﹣4y+1　．
【分析】根据积除以一个因式得到另一个因式即可．
【解答】解：根据题意得：（﹣6x2y2+8xy2﹣2xy）÷（﹣2xy）＝3xy﹣4y+1，
故答案为：3xy﹣4y+1
【点评】此题考查了单项式乘多项式，熟练掌握运算法则是解本题的关键．
10．填空：
（1）（﹣3x2）（﹣x2+2x﹣1）＝　3x4﹣6x3+3x2　；
（2）﹣（2x﹣4x3﹣8）?（﹣x2）＝　x3﹣2x5﹣4x2　；
（3）2（a2b2﹣ab+1）+3ab（1﹣ab）＝　2+ab﹣a2b2　；
（4）（﹣3x2）（x2﹣2x﹣3）+3x（x3﹣2x2﹣5）＝　9x2﹣15x　；
（5）8m（m2﹣3m+4）﹣m2（m﹣3）＝　7m3﹣21m2+32m　；
（6）7x（2x﹣1）﹣3x（4x﹣1）﹣2x（x+3）+1＝　2x2﹣4x　；
（7）（﹣2a2b）2（ab2﹣a2b+a3）＝　4a5b4﹣4a6b3+4a7b2　；
（8）﹣（﹣x）2?（﹣2x2y）3+2x2（x6y3﹣1）＝　2x4y+2x8y3﹣2x2　．
【分析】根据单项式与多项式相乘的运算法则进行计算即可．
【解答】解：（1）（﹣3x2）（﹣x2+2x﹣1）＝3x4﹣6x3+3x2；
（2）﹣（2x﹣4x3﹣8）?（﹣x2）＝x3﹣2x5﹣4x2；
（3）2（a2b2﹣ab+1）+3ab（1﹣ab）＝2a2b2﹣2ab+2+3ab﹣3a2b2＝2+ab﹣a2b2；
（4）（﹣3x2）（x2﹣2x﹣3）+3x（x3﹣2x2﹣5）＝﹣3x4+6x3+9x2+3x4﹣6x3﹣15x＝9x2﹣15x；
（5）8m（m2﹣3m+4）﹣m2（m﹣3）＝8m3﹣24m2+32m﹣m3+3m2＝7m3﹣21m2+32m；
（6）7x（2x﹣1）﹣3x（4x﹣1）﹣2x（x+3）+1＝14x2﹣7x﹣12x2+3x＝2x2﹣4x；
（7）（﹣2a2b）2（ab2﹣a2b+a3）＝4a5b4﹣4a6b3+4a7b2；
（8）﹣（﹣x）2?（﹣2x2y）3+2x2（x6y3﹣1）＝2x4y+2x8y3﹣2x2．
故答案为：（1）3x4﹣6x3+3x2；（2）x3﹣2x5﹣4x2；（3）2+ab﹣a2b2；（4）9x2﹣15x；（5）7m3﹣21m2+32m；（6）2x2﹣4x；（7）4a5b4﹣4a6b3+4a7b2；（8）2x4y+2x8y3﹣2x2．
【点评】本题考查的是单项式与多项式相乘的运算法则：单项式与多项式相乘，就是用单项式去乘多项式的每一项，再把所得的积相加．
11．若M＝（x﹣2）（x﹣8），N＝（x﹣3）（x﹣7），则M﹣N＝　﹣5　．
【分析】先算乘法，再去括号合并同类项，即可得出答案．
【解答】解：∵M＝（x﹣2）（x﹣8），N＝（x﹣3）（x﹣7），
∴M﹣N＝（x2﹣10x+16）﹣（x2﹣10x+21）
＝﹣5，
故答案：﹣5．
【点评】本题考查了多项式乘以多项式，能熟记多项式乘以多项式法则是解此题的关键．
12．若a的值使得x2+4x+a＝（x﹣5）（x+9）﹣2成立，则a的值为　﹣47　．
【分析】首先利用多项式与多项式相乘的法则：多项式与多项式相乘，先用一个多项式的每一项乘另外一个多项式的每一项，再把所得的积相加计算（x﹣5）（x+9）﹣2，然后可得答案．
【解答】解：（x﹣5）（x+9）﹣2＝x2+4x﹣45﹣2＝x2+4x﹣47，
∵x2+4x+a＝（x﹣5）（x+9）﹣2，
∴a＝﹣47，
故答案为：﹣47．
【点评】此题主要考查了多项式乘以多项式，关键是掌握计算法则．
13．如图，正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼一个长为（a+3b），宽为（2a+b）的长方形，则需要C类卡片　7　张．

【分析】根据长方形的面积＝长×宽，求出长为a+3b，宽为2a+b的大长方形的面积是多少，判断出需要A类、B类、C类卡片各多少张即可．
【解答】解：∵（a+3b）（2a+b）＝2a2+ab+6ab+3b2＝2a2+7ab+3b2，
∴需要A类卡片2张、B类卡片3张、C类卡片7张，
故答案为：7．
【点评】此题主要考查了多项式乘多项式的运算方法，熟练掌握运算法则是解题的关键．
14．如图，有多个长方形和正方形的卡片，图甲是选取了2块不同的卡片，拼成的一个图形，借助图中阴影部分面积的不同表示可以用来验证等式a（a+b）＝a2+ab成立，根据图乙，利用面积的不同表示方法，仿照上边的式子写出一个等式　（a+b）（a+2b）＝a2+3ab+2b2　．

【分析】根据多项式乘多项式，利用第一个多项式的每一项乘以第二个多项式的每一项，把所得积相加，可得答案．
【解答】解：由图示，得
（a+b）（a+2b）＝a2+3ab+2b2，
故答案为：（a+b）（a+2b）＝a2+3ab+2b2．
【点评】本题考查了多项式乘多项式，熟记法则并根据法则计算是解题关键．
三．解答题（共6小题）
15．（1）化简：4m+2（m﹣2n）
（2）（2x）3﹣6x（x2+2x﹣1）．
【分析】（1）直接去括号，进而合并同类项得出答案；
（2）直接去括号，进而合并同类项得出答案．
【解答】解：（1）4m+2（m﹣2n）
＝4m+2m﹣4n
＝6m﹣4n；

（2）原式＝8x3﹣（6x3+12x2﹣6x）
＝8x3﹣6x3﹣12x2+6x
＝2x3﹣12x2+6x．
【点评】此题主要考查了整式的加减运算，正确合并同类项是解题关键．
16．（1）已知（﹣2x2）（3x2﹣ax﹣6）﹣3x3+x2中不含x的三次项，求a的值．
（2）按村镇建设规划的要求，需将小张家一块正方形土地的一边增加5米，另一边减少5米，这块土地的面积改变了吗？请说明理由．
【分析】（1）原式利用单项式乘以多项式法则计算，整理后根据结果不含x的三次项，求出a的值即可；
（2）由题意可知道原来正方形土地的面积是x2平方米，而现在这块地的一边增加5米，另一边减少5米后的面积是（x+5）（x﹣5）平方米，然后用x2减去（x+5）（x﹣5）算出答案即可．
【解答】解：（1）（﹣2x2）（3x2﹣ax﹣6）﹣3x3+x2
＝﹣6x4+2ax3+12x2﹣3x3+x2
＝﹣6x4+（2a﹣3）x3+13x2，
∵不含x的三次项，
∴2a﹣3＝0，
解得a＝；
（2）设原来正方形土地的边长是x米，则原来正方形土地的面积是x2平方米，
现在这块地的一边增加5米，另一边减少5米后的面积是（x+5）（x﹣5）平方米，
∴x2﹣（x+5）（x﹣5）＝x2﹣（x2﹣25）＝25，
∴这块土地的面积改变了．
【点评】（1）考查了整式的混合运算，熟练掌握运算法则是解本题的关键．
（2）考查了平方差公式在生活实际中的运用，解题的关键就是读懂题意列出算式，然后熟练的运用平方差公式（a+b）（a﹣b）＝a2﹣b2进行计算．
17．如图甲、乙两个农民共有4块地，今年他们决定共同搞投资饲养业，为此他们准备将这4块地换成宽为（a+b）m的地，为了使所换到的面积与原来地的总面积相等，交换之后的地的长应为多少m．

【分析】先求出原4块地的总面积，再分解因式，即可得出答案．
【解答】解：∵原来4块地的总面积为（a2+bc+ac+ab）m2
∴a2+bc+ac+ab＝a（a+b）+c（a+b）＝（a+b）（a+c），
∵此块地的宽为（a+b）m，
∴交换后这块土地的长为（a+c）m．
【点评】本题考查了单项式乘以多项式，因式分解的应用，能正确分解因式是解此题的关键．
18．探究应用：
（1）计算：（x+1）（x2﹣x+1）＝　x3+1　；（2x+y）（4x2﹣2xy+y2）＝　8x3+y3　．
（2）上面的乘法计算结果很简洁，你发现了什么规律（公式）？用含a、b的字母表示该公式为：　（a+b）（a2﹣ab+b2）＝a3+b3　．
（3）下列各式能用第（2）题的公式计算的是　C　．
A．（m+2）（m2+2m+4）B．（m+2n）（m2﹣2mn+2n2）
C．（3+n）（9﹣3n+n2） D．（m+n）（m2﹣2mn+n2）
【分析】根据多项式乘以多项式的法则即可计算出答案．
【解答】解：（1）（x+1）（x2﹣x+1）＝x3﹣x2+x+x2﹣x+1＝x3+1，
（2x+y）（4x2﹣2xy+y2）＝8x3﹣4x2y+2xy2+4x2y﹣2xy2+y3＝8x3+y3，
（2）（a+b）（a2﹣ab+b2）＝a3+b3；
（3）由（2）可知选（C）；
故答案为：（1）x3+1；8x3+y3；（2）（a+b）（a2﹣ab+b2）＝a3+b3；（3）（C）
【点评】本题考查多项式乘以多项式，同时考查学生的观察归纳能力，属于基础题型．
19．如图，某市有一块长为（3a+b）米，宽为（2a+b）米的长方形地块，规划部门计划将阴影部分进行绿化，中间将修建一座雕像，则绿化的面积是多少平方米？并求出当a＝3，b＝2时的绿化面积．

【分析】根据多项式乘多项式的法则求出阴影部分的面积，代入计算即可．
【解答】解：阴影部分的面积＝（3a+b）（2a+b）﹣（a+b）2
＝6a2+5ab+b2﹣a2﹣2ab﹣b2
＝5a2+3ab，
当a＝3，b＝2时，原式＝5×32+3×3×2＝63（平方米）．
【点评】本题考查的是多项式乘多项式，多项式与多项式相乘的法则：多项式与多项式相乘，先用一个多项式的每一项乘另外一个多项式的每一项，再把所得的积相加．
20．欢欢与乐乐两人共同计算（2x+a）（3x+b），欢欢抄错为（2x﹣a）（3x+b），得到的结果为6x2﹣13x+6；乐乐抄错为（2x+a）（x+b），得到的结果为2x2﹣x﹣6．
（1）式子中的a、b的值各是多少？
（2）请计算出原题的正确答案．
【分析】（1）根据由于欢欢抄错了第一个多项式中的a符号，得出的结果为6x2﹣13x+6，可知（2x﹣a）（3x+b）＝6x2+（2b﹣3a）x﹣ab＝6x2﹣13x+6，于是2b﹣3a＝﹣13①；再根据乐乐由于漏抄了第二个多项式中的x的系数，得到的结果为2x2﹣x﹣6，可知常数项是﹣6，可知（2x+a）（x+b）＝2x2﹣x﹣6，可得到2b+a＝﹣1②，解关于①②的方程组即可求出a、b的值；
（2）把a、b的值代入原式求出整式乘法的正确结果．
【解答】解：（1）根据题意可知，由于欢欢抄错了第一个多项式中的a的符号，得到的结果为6x2﹣13x+6，
那么（2x﹣a）（3x+b）＝6x2+（2b﹣3a）x﹣ab＝6x2﹣13x+6，
可得2b﹣3a＝﹣13 ①
乐乐由于漏抄了第二个多项式中的x的系数，得到的结果为2x2﹣x﹣6，
可知（2x+a）（x+b）＝2x2﹣x﹣6
即2x2+（2b+a）x+ab＝2x2﹣x﹣6，
可得2b+a＝﹣1 ②，
解关于①②的方程组，可得a＝3，b＝﹣2；
（2）正确的式子：
（2x+3）（3x﹣2）＝6x2+5x﹣6
【点评】本题主要是考查多项式的乘法，正确利用法则是正确解决问题的关键．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布
日期：2019/1/31 5:08:10；用户：zhrasce20；邮箱：zhrasce20@163.com；学号：6322261




















21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）



HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)