6.4 频数与频率同步练习

中小学教育资源及组卷应用平台


绝密★启用前
浙教版七下同步练习第六章数据与统计图表
6.4 频数与频率
题号 一 二 三 总分
得分
注意事项：
1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上
第Ⅰ卷（选择题）
请点击修改第I卷的文字说明
评卷人 得 分

一．选择题（共8小题）
1．我校学生会成员的年龄如下表：则出现频数最多的年龄是（　　）
年 龄 13 14 15 16
人数（人） 4 5 4 3
A．4 B．14 C．13和15 D．2
2．酷爱打球的小王3分钟共投篮80次，进了64个球，小王进球的频率是（　　）
A．1.2 B．0.8 C．64 D．80
3．某样本容量是60，分组后，第2组的频率是0.15，那么第2组的频数是（　　）
A．9 B．18 C．60 D．400
4．下列各数：﹣6.1，﹣||，﹣（﹣1），（﹣2）2，（﹣5）3，﹣3×5×（﹣6）中，负数出现的频率为（　　）
A．66.7% B．83.3% C．50% D．33.3%
5．已知一个样本27，23，25，27，29，31，27，30，32，28，31，28，26，27，29，18，24，26，27，30，那么频数为8的范围是（　　）
A．24.5～26.5 B．26.5～28.5 C．28.5～30.5 D．30.5～32.5
6．某市体育协会对2400名年满15岁的男生的身高进行了测量，结果身高（单位：m）在1.68﹣1.70这一小组的频率为0.25，则该组的人数为（　　）
A．600人 B．250人 C．60人 D．25人
7．一个样本有若干个数据，分为5组，第三组的频数为12，频率为15%，样本容量是（　　）
A．60 B．75 C．80 D．180
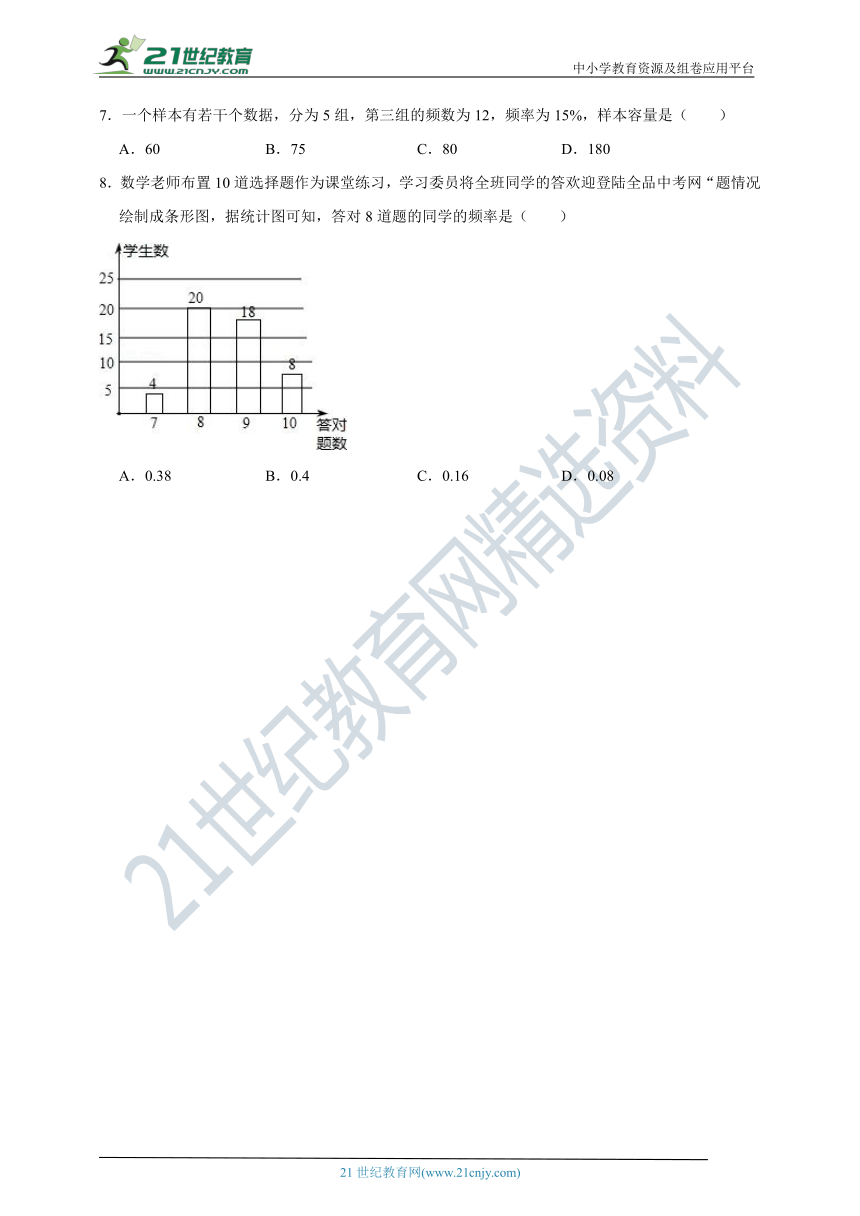
8．数学老师布置10道选择题作为课堂练习，学习委员将全班同学的答欢迎登陆全品中考网“题情况绘制成条形图，据统计图可知，答对8道题的同学的频率是（　　）

A．0.38 B．0.4 C．0.16 D．0.08



第Ⅱ卷（非选择题）
请点击修改第Ⅱ卷的文字说明
评卷人 得 分

二．填空题（共6小题）
9．一只不透明的袋子中装有红球和白球共30个，这些球除了颜色外都相同，校课外学习小组做摸球实验，将球搅匀后任意摸出一个球，记下颜色后放回，搅匀，通过多次重复试验，算得摸到红球的频率是0.2，则袋中有　 　个红球．
10．有5张看上去无差别的卡片，上面分别写着0，π，，，1.333，随机抽取1张，做了2000次实验，则取出的数是无理数的频率是　 　．
11．对某校八年级（1）班50名同学的一次数学测验成绩进行统计，如果80.5﹣90.5分这一组的频数是18，那么这个班的学生这次数学测验成绩在80.5﹣90.5分之间的频率是　 　．
12．新吴区举行迎五一歌咏比赛，组委会规定：任何一名参赛选手的成绩x需满足60≤x＜100，赛后整理所有参赛选手的成绩如下表．根据表中提供的信息得到n＝　 　．
分数段 频数 频率
60≤x＜70 30 0.15
70≤x＜80 m 0.45
80≤x＜90 60 n
90≤x＜100 20 0.1
13．某养鱼专业户为了估测鱼的质量，从鱼池中捕捞10条鱼，称得每条鱼的质量如下：（单位：kg）1.2，1.1，1.1，1.0，1.1，1.2，1.1，1.2，1.1，1.0．则这些鱼的质量中频数最大的质量是　 　，其频率是　 　．
14．我市某校40名学生参加全国数学竞赛，把他们的成绩分为6组，第一组到第四组的频数分别为10，5，7，6，第五组的频率是0.2，则第六组的频率是　 　．
评卷人 得 分

三．解答题（共6小题）
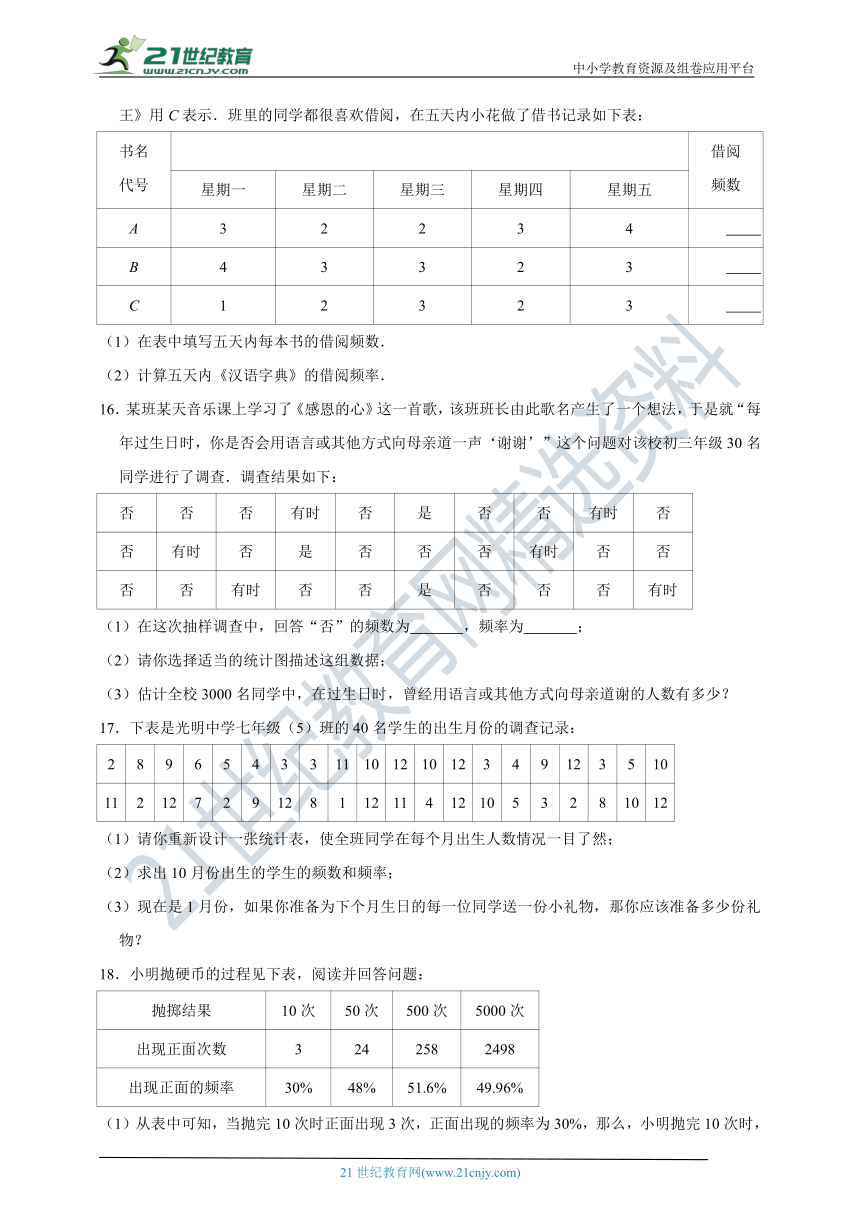
15．小花最近买了三本课外书，分别是《汉语字典》用A表示，《流行杂志》用B表示和《故事大王》用C表示．班里的同学都很喜欢借阅，在五天内小花做了借书记录如下表：
书名代号 借阅频数
星期一 星期二 星期三 星期四 星期五
A 3 2 2 3 4 　 　
B 4 3 3 2 3 　 　
C 1 2 3 2 3 　 　
（1）在表中填写五天内每本书的借阅频数．
（2）计算五天内《汉语字典》的借阅频率．
16．某班某天音乐课上学习了《感恩的心》这一首歌，该班班长由此歌名产生了一个想法，于是就“每年过生日时，你是否会用语言或其他方式向母亲道一声‘谢谢’”这个问题对该校初三年级30名同学进行了调查．调查结果如下：
否 否 否 有时 否 是 否 否 有时 否
否 有时 否 是 否 否 否 有时 否 否
否 否 有时 否 否 是 否 否 否 有时
（1）在这次抽样调查中，回答“否”的频数为　 　，频率为　 　；
（2）请你选择适当的统计图描述这组数据；
（3）估计全校3000名同学中，在过生日时，曾经用语言或其他方式向母亲道谢的人数有多少？
17．下表是光明中学七年级（5）班的40名学生的出生月份的调查记录：
2 8 9 6 5 4 3 3 11 10 12 10 12 3 4 9 12 3 5 10
11 2 12 7 2 9 12 8 1 12 11 4 12 10 5 3 2 8 10 12
（1）请你重新设计一张统计表，使全班同学在每个月出生人数情况一目了然；
（2）求出10月份出生的学生的频数和频率；
（3）现在是1月份，如果你准备为下个月生日的每一位同学送一份小礼物，那你应该准备多少份礼物？
18．小明抛硬币的过程见下表，阅读并回答问题：
抛掷结果 10次 50次 500次 5000次
出现正面次数 3 24 258 2498
出现正面的频率 30% 48% 51.6% 49.96%
（1）从表中可知，当抛完10次时正面出现3次，正面出现的频率为30%，那么，小明抛完10次时，得到　 　次反面，反面出现的频率是　 　；
（2）当他抛完5000次时，反面出现的次数是　 　，反面出现的频率是　 　；
（3）通过上面我们可以知道，正面出现的频数和反面出现的频数之和等于　 　，正面出现的频率和反面出现的频率之和等于　 　．
19．在某项针对18～35岁的青年人每天发微博数量的调查中，设一个人的“日均发微博条数”为m，规定：当m≥10时为A级，当5≤m＜10时为B级，当0≤m＜5时为C级．现随机抽取30个符合年龄条件的青年人开展每人“日均发微博条数”的调查，所抽青年人的“日均发微博条数”的数据如下：
11 10 6 15 9 16 13 12 0 8
2 8 10 17 6 13 7 5 7 3
12 10 7 11 3 6 8 14 15 12
（1）求样本数据中为A级的频率；
（2）试估计1000个18～35岁的青年人中“日均发微博条数”为A级的人数．
20．食品安全问题已经严重影响到我们的健康．某执法部门最近就食品安全抽样调查某一家超市，从中随机抽样选取20种包装食品，并列出下表：
食品质量 优 良 合格 不合格 有害或有毒食品
数量 0 2 3 n 4
请你根据以上信息解答下列问题：
（1）这次抽样调查中，“食品质量为合格以上（含合格）”的频率为　 　；
（2）若这家超市经销的包装食品共有1300种，请你估计大约有多少种包装食品是“有害或有毒”的？



参考答案与试题解析
一．选择题（共8小题）
1．我校学生会成员的年龄如下表：则出现频数最多的年龄是（　　）
年 龄 13 14 15 16
人数（人） 4 5 4 3
A．4 B．14 C．13和15 D．2
【分析】频数是指每个对象出现的次数，从而结合表格可得出出现频数最多的年龄．
【解答】解：由表格可得，14岁出现的人数最多，
故出现频数最多的年龄是14岁．
故选：B．
【点评】此题考查了频数和频率的知识，掌握频数是指每个对象出现的次数是解答本题的关键，难度一般．
2．酷爱打球的小王3分钟共投篮80次，进了64个球，小王进球的频率是（　　）
A．1.2 B．0.8 C．64 D．80
【分析】根据概率的意义，可得答案．
【解答】解：由题意得
小王进球的频率是64÷80＝0.8，
故选：B．
【点评】本题是对频率、频数灵活运用的综合考查，频率＝．
3．某样本容量是60，分组后，第2组的频率是0.15，那么第2组的频数是（　　）
A．9 B．18 C．60 D．400
【分析】利用频数＝频率×样本容量直接计算即可．
【解答】解：∵样本容量是60，分组后，第2组的频率是0.15，
∴第2组的频数是60×0.15＝9，
故选：A．
【点评】本题考查了频数与频率的知识，解题的关键是能够了解它们之间的关系，难度不大．
4．下列各数：﹣6.1，﹣||，﹣（﹣1），（﹣2）2，（﹣5）3，﹣3×5×（﹣6）中，负数出现的频率为（　　）
A．66.7% B．83.3% C．50% D．33.3%
【分析】首先熟练将各个数据化简，然后找到其中的负数个数；再根据频率＝频数÷总数进行计算．
【解答】解：将各数化简，即有
﹣6.1，﹣，1，4，﹣125，90．
显然6个数中，有3个负数．
故负数出现的频率是3÷6＝50%．
故选：C．
【点评】本题考查频数与频率，频数是指每个对象出现的次数．频率是指每个对象出现的次数与总次数的比值（或者百分比）．即频率＝频数÷数据总数．也考查了相反数、绝对值、有理数的乘方．
5．已知一个样本27，23，25，27，29，31，27，30，32，28，31，28，26，27，29，18，24，26，27，30，那么频数为8的范围是（　　）
A．24.5～26.5 B．26.5～28.5 C．28.5～30.5 D．30.5～32.5
【分析】根据题意可得共20个数据，其中在26.5～28.5之间的有8个，其频数为8．
【解答】解：根据所给数据可得在26.5～28.5之间的有8个，那么频数为8的范围是26.5～28.5，
故选：B．
【点评】此题主要考查了频数，频数是指每个对象出现的次数．
6．某市体育协会对2400名年满15岁的男生的身高进行了测量，结果身高（单位：m）在1.68﹣1.70这一小组的频率为0.25，则该组的人数为（　　）
A．600人 B．250人 C．60人 D．25人
【分析】根据频数＝频率×数据总和进行解答即可．
【解答】解：由题意，该组的人数为：2400×0.25＝600（人）．
故选：A．
【点评】本题考查了频数与频率之间的计算，熟知频数、频率及样本总数之间的关系是解决本题的关键．
7．一个样本有若干个数据，分为5组，第三组的频数为12，频率为15%，样本容量是（　　）
A．60 B．75 C．80 D．180
【分析】根据总数据个数＝第三组的频数：第三组的频率，列出算式计算，进一步可得样本容量．
【解答】解：样本容量为12÷15%＝80．
故选：C．
【点评】本题考查了频率的计算公式，理解公式是关键．
8．数学老师布置10道选择题作为课堂练习，学习委员将全班同学的答欢迎登陆全品中考网“题情况绘制成条形图，据统计图可知，答对8道题的同学的频率是（　　）

A．0.38 B．0.4 C．0.16 D．0.08
【分析】根据条形统计图求出总共答对的人数，再求出答对8道题的同学人数，然后利用答对8道题的同学人数÷总共的人数，即可得出答案．
【解答】解：总共的人数有4+20+18++8＝50人，
答对8道题的同学有20人，
∴答对8道题以上的同学的频率是：20÷50＝0.4，
故选：B．
【点评】此题主要考查了条形统计图的应用，利用条形图得出总共答对的人数与答对8道题的同学人数是解题关键．
二．填空题（共6小题）
9．一只不透明的袋子中装有红球和白球共30个，这些球除了颜色外都相同，校课外学习小组做摸球实验，将球搅匀后任意摸出一个球，记下颜色后放回，搅匀，通过多次重复试验，算得摸到红球的频率是0.2，则袋中有　6　个红球．
【分析】在同样条件下，大量反复试验时，随机事件发生的频率逐渐稳定在概率附近，可以从比例关系入手，列出方程求解．
【解答】解：设袋中有x个红球．
由题意可得：＝0.2，
解得：x＝6，
即袋中有6个红球，
故答案为：6．
【点评】此题主要考查了利用频率估计概率，本题利用了用大量试验得到的频率可以估计事件的概率．关键是根据红球的频率得到相应的等量关系．
10．有5张看上去无差别的卡片，上面分别写着0，π，，，1.333，随机抽取1张，做了2000次实验，则取出的数是无理数的频率是　0.4　．
【分析】无理数的个数除以实数的总个数，即为所求的频率．
【解答】解：所有的数有5个，其中无理数有π，，共2个，
∴取出的数是无理数的频率是2÷5＝0.4．
故答案为：0.4
【点评】本题考查了频率，频率是指每个对象出现的次数与总次数的比值（或者百分比）．判断出无理数的个数是解决本题的易错点．
11．对某校八年级（1）班50名同学的一次数学测验成绩进行统计，如果80.5﹣90.5分这一组的频数是18，那么这个班的学生这次数学测验成绩在80.5﹣90.5分之间的频率是　0.36　．
【分析】根据频率与频数的关系求出所求即可．
【解答】解：根据题意得：18÷50＝0.36，
故答案为：0.36
【点评】此题考查了频率与频数，弄清频率与频数之间的关系是解本题的关键．
12．新吴区举行迎五一歌咏比赛，组委会规定：任何一名参赛选手的成绩x需满足60≤x＜100，赛后整理所有参赛选手的成绩如下表．根据表中提供的信息得到n＝　0.3　．
分数段 频数 频率
60≤x＜70 30 0.15
70≤x＜80 m 0.45
80≤x＜90 60 n
90≤x＜100 20 0.1
【分析】根据各分数段的频率之和等于1可得答案．
【解答】解：n＝1﹣（0.15+0.45+0.1）＝0.3，
故答案为：0.3
【点评】本题主要考查频数与频率，解题的关键是掌握频数之和等于总数、频率之和为1．
13．某养鱼专业户为了估测鱼的质量，从鱼池中捕捞10条鱼，称得每条鱼的质量如下：（单位：kg）1.2，1.1，1.1，1.0，1.1，1.2，1.1，1.2，1.1，1.0．则这些鱼的质量中频数最大的质量是　1.1　，其频率是　0.5　．
【分析】能够从所给数据中找到称得质量为1.1千克的鱼的频数；再根据频率＝频数÷总数，进行计算．
【解答】解：根据题意，得
从鱼塘中捞捕10条鱼，其中有5条是1.1千克；
故称得质量为1.1千克的鱼的频率为＝0.5．
故答案为：1.1，0.5．
【点评】本题考查频率、频数的关系：频率＝，解决本题的关键是熟记频率、频数的关系．
14．我市某校40名学生参加全国数学竞赛，把他们的成绩分为6组，第一组到第四组的频数分别为10，5，7，6，第五组的频率是0.2，则第六组的频率是　0.1　．
【分析】本题已知数据总个数和前四个组的频数，只要求出第五组的频数；就可用总数据40减去第一至第五组的频数，求出第六组的频数，从而求得第六组的频率．
【解答】解：因为共有40个数据，且第五组的频率为0.2，所以第五组的频数为0.2×40＝8；
则第六组的频数为40﹣（10+5+7+6+8）＝4，所以第六组的频率为＝0.1，
故答案为：0.1．
【点评】本题是对频率、频数灵活运用的综合考查，注意：每个小组的频数等于数据总数减去其余小组的频数，即各小组频数之和等于数据总和，频率＝．
三．解答题（共6小题）
15．小花最近买了三本课外书，分别是《汉语字典》用A表示，《流行杂志》用B表示和《故事大王》用C表示．班里的同学都很喜欢借阅，在五天内小花做了借书记录如下表：
书名代号 借阅频数
星期一 星期二 星期三 星期四 星期五
A 3 2 2 3 4 　14　
B 4 3 3 2 3 　15　
C 1 2 3 2 3 　11　
（1）在表中填写五天内每本书的借阅频数．
（2）计算五天内《汉语字典》的借阅频率．
【分析】（1）从星期一到星期五的借阅次数的和就是频数；
（2）求得借阅三种书的频数的总和，然后利用频率公式即可求解．
【解答】解：（1）填表如下：
书名代号 借阅频数
星期一 星期二 星期三 星期四 星期五
A 3 2 2 3 4 14
B 4 3 3 2 3 15
C 1 2 3 2 3 11
（2）总数是14+15+11＝40，则五天内《汉语字典》的借阅频率是：＝．
【点评】本题是对频率、频数灵活运用的综合考查．注意：每个小组的频数等于数据总数减去其余小组的频数，即各小组频数之和等于数据总和．频率＝．
16．某班某天音乐课上学习了《感恩的心》这一首歌，该班班长由此歌名产生了一个想法，于是就“每年过生日时，你是否会用语言或其他方式向母亲道一声‘谢谢’”这个问题对该校初三年级30名同学进行了调查．调查结果如下：
否 否 否 有时 否 是 否 否 有时 否
否 有时 否 是 否 否 否 有时 否 否
否 否 有时 否 否 是 否 否 否 有时
（1）在这次抽样调查中，回答“否”的频数为　21　，频率为　0.7　；
（2）请你选择适当的统计图描述这组数据；
（3）估计全校3000名同学中，在过生日时，曾经用语言或其他方式向母亲道谢的人数有多少？
【分析】（1）数出回答否的人数，就是频数，频数除以30就是频率．
（2）可用条形统计图来描述．
（3）计算出是、及有时的频率，然后根据频数＝总数×频率即可得出答案．
【解答】解：（1）说“否”的有21人，故频数为21，频率＝21÷30＝0.7．
（2）说否的有21人，说是的有3人，说有时的有6人．

（3）是、有时的频率＝，
∴全校3000名同学中，在过生日时，曾经用语言或其他方式向母亲道谢的人数＝3000×＝900人．
【点评】本题考查画条形图，因为条形图表现每组里面具体的数据，以及频数，频率概念的掌握情况．
17．下表是光明中学七年级（5）班的40名学生的出生月份的调查记录：
2 8 9 6 5 4 3 3 11 10 12 10 12 3 4 9 12 3 5 10
11 2 12 7 2 9 12 8 1 12 11 4 12 10 5 3 2 8 10 12
（1）请你重新设计一张统计表，使全班同学在每个月出生人数情况一目了然；
（2）求出10月份出生的学生的频数和频率；
（3）现在是1月份，如果你准备为下个月生日的每一位同学送一份小礼物，那你应该准备多少份礼物？
【分析】（1）根据题意，按生日的月份重新分组统计可得表格；
（2）根据频数与频率的概念可得答案；
（3）根据频数的概念，读表可得2月份生日的频数，即可得答案．
【解答】解：（1）按生日的月份重新分组可得统计表：
月份 1 2 3 4 5 6 7 8 9 10 11 12
人数 1 4 5 3 3 1 1 3 3 5 3 8
（2）读表可得：10月份出生的学生的频数是5，频率为＝0.125
（3）2月份有4位同学过生日，因此应准备4份礼物．
【点评】本题考查频率、频数的定义及频率的计算方法．
18．小明抛硬币的过程见下表，阅读并回答问题：
抛掷结果 10次 50次 500次 5000次
出现正面次数 3 24 258 2498
出现正面的频率 30% 48% 51.6% 49.96%
（1）从表中可知，当抛完10次时正面出现3次，正面出现的频率为30%，那么，小明抛完10次时，得到　7　次反面，反面出现的频率是　70%　；
（2）当他抛完5000次时，反面出现的次数是　2502　，反面出现的频率是　50.04%　；
（3）通过上面我们可以知道，正面出现的频数和反面出现的频数之和等于　抛掷总次数　，正面出现的频率和反面出现的频率之和等于　1　．
【分析】频数即一组数据中出现数据的个数，频率＝频数÷总数．
【解答】解：（1）当抛完10次时正面出现3次，正面出现的频率为30%，那么小明抛完10次时，得到7次反面，反面出现的频率是70%；
（2）当他抛完5000次时，反面出现的次数是2502，反面出现的频率是50.04%；
（3）正面出现的频数和反面出现的频数之和等于抛掷总次数，正面出现的频率和反面出现的频率之和等于1．
【点评】理解频数的概念，掌握频数的计算方法．注意各个小组的频数和等于数据总数，各个小组的频率和是1．
19．在某项针对18～35岁的青年人每天发微博数量的调查中，设一个人的“日均发微博条数”为m，规定：当m≥10时为A级，当5≤m＜10时为B级，当0≤m＜5时为C级．现随机抽取30个符合年龄条件的青年人开展每人“日均发微博条数”的调查，所抽青年人的“日均发微博条数”的数据如下：
11 10 6 15 9 16 13 12 0 8
2 8 10 17 6 13 7 5 7 3
12 10 7 11 3 6 8 14 15 12
（1）求样本数据中为A级的频率；
（2）试估计1000个18～35岁的青年人中“日均发微博条数”为A级的人数．
【分析】（1）先找出数据中A级的频数，用频数÷总数即可求得频率；
（2）用总人数×频率即可估算A级的人数．
【解答】解：（1）m≥10的人数有15人，
则频率＝＝；
（2）1000×＝500（人），
即1000个18～35岁的青年人中“日均发微博条数”为A级的人数为500人．
【点评】本题考查了频数和频率，注意掌握频率＝．
20．食品安全问题已经严重影响到我们的健康．某执法部门最近就食品安全抽样调查某一家超市，从中随机抽样选取20种包装食品，并列出下表：
食品质量 优 良 合格 不合格 有害或有毒食品
数量 0 2 3 n 4
请你根据以上信息解答下列问题：
（1）这次抽样调查中，“食品质量为合格以上（含合格）”的频率为　0.25　；
（2）若这家超市经销的包装食品共有1300种，请你估计大约有多少种包装食品是“有害或有毒”的？
【分析】（1）首先求出随机抽样的20种包装食品中“食品质量为合格以上（含合格）”的数量，然后根据频率＝频数÷数据总数得出结果；
（2）首先求出随机抽样的20种包装食品中“有害或有毒”的频率，然后根据样本估计总体的思想，得出答案．
【解答】解：（1）∵这次抽样中，食品质量为合格以上（含合格）”的频数是0+2+3＝5，
∴频率为 ＝0.25；

（2）1300×＝260种．
答：约有260种包装食品是“有害或有毒”的．
【点评】本题考查的是频率的计算公式及通过样本去估计总体．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布
日期：2019/2/1 21:04:53；用户：zhrasce20；邮箱：zhrasce20@163.com；学号：6322261
























21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）



HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)