6.5 频数直方图同步练习

中小学教育资源及组卷应用平台


绝密★启用前
浙教版七下同步练习第六章数据与统计图表
6.5 频数直方图
题号 一 二 三 总分
得分
注意事项：
1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上
第Ⅰ卷（选择题）
请点击修改第I卷的文字说明
评卷人 得 分

一．选择题（共8小题）
1．如图，是某中学九（3）班学生外出方式（乘车、步行、骑车）的不完整频数（人数）分布直方图．如果乘车的频率是0.4，那么步行的频率为（　　）

A．0.4 B．0.36 C．0.3 D．0.24
2．如图是某班45名同学爱心捐款额的频数分布直方图（每组含前一个边界值，不含后一个边界值），则捐款人数最多的一组是（　　）

A．5～10元 B．10～15元 C．15～20元 D．20～25元
3．一个容量为80的样本最大值为143，最小值为50，取组距为10，则可以分成（　　）
A．10组 B．9组 C．8组 D．7组
4．某校初中三年级共有学生400人，为了解这些学生的视力情况，抽查了20名学生的视力，对所得数据进行整理，在得到的频数分布表中，若数据在0.95～1.15这一小组的频率为0.3，则可估计该校初中三年级学生视力在0.95～1.15范围内的人数约为（　　）
A．6人 B．30人 C．60人 D．120人
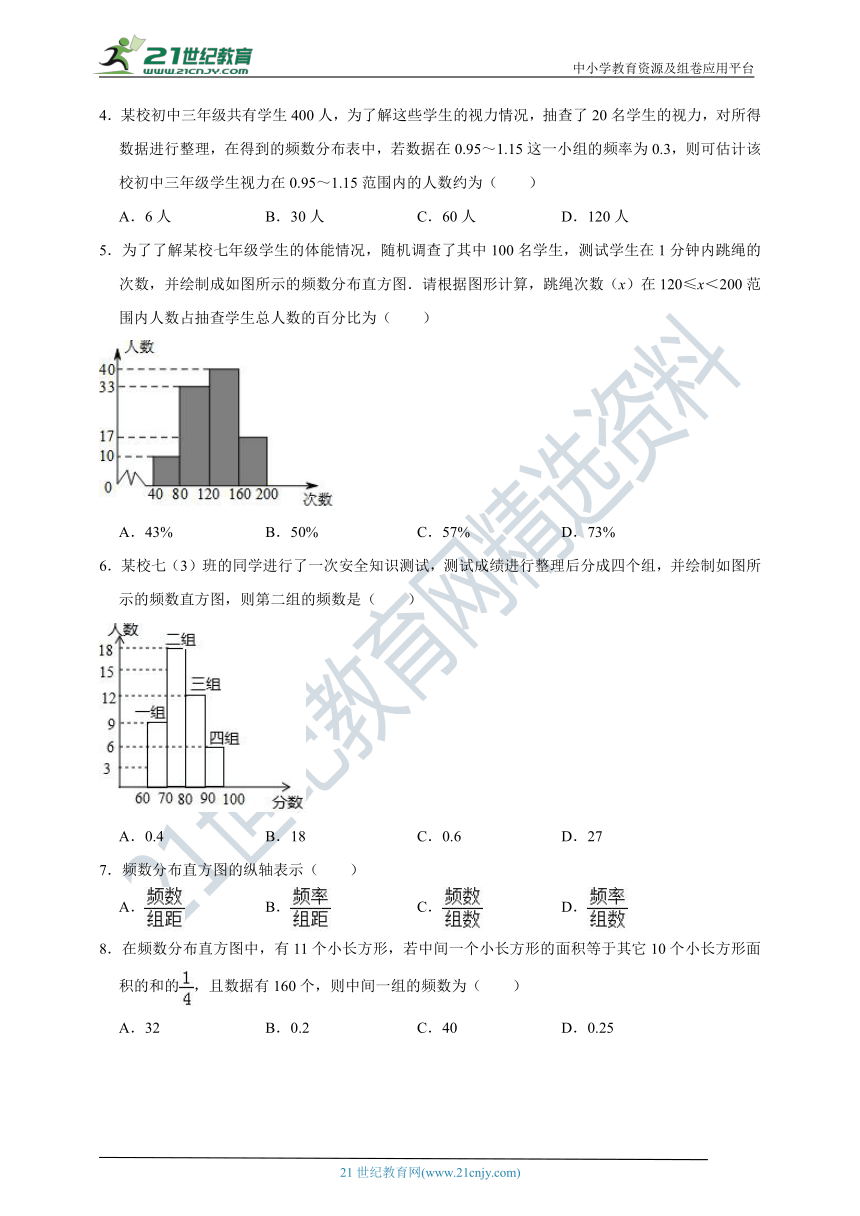
5．为了了解某校七年级学生的体能情况，随机调查了其中100名学生，测试学生在1分钟内跳绳的次数，并绘制成如图所示的频数分布直方图．请根据图形计算，跳绳次数（x）在120≤x＜200范围内人数占抽查学生总人数的百分比为（　　）

A．43% B．50% C．57% D．73%
6．某校七（3）班的同学进行了一次安全知识测试，测试成绩进行整理后分成四个组，并绘制如图所示的频数直方图，则第二组的频数是（　　）

A．0.4 B．18 C．0.6 D．27
7．频数分布直方图的纵轴表示（　　）
A． B． C． D．
8．在频数分布直方图中，有11个小长方形，若中间一个小长方形的面积等于其它10个小长方形面积的和的，且数据有160个，则中间一组的频数为（　　）
A．32 B．0.2 C．40 D．0.25



第Ⅱ卷（非选择题）
请点击修改第Ⅱ卷的文字说明
评卷人 得 分

二．填空题（共6小题）
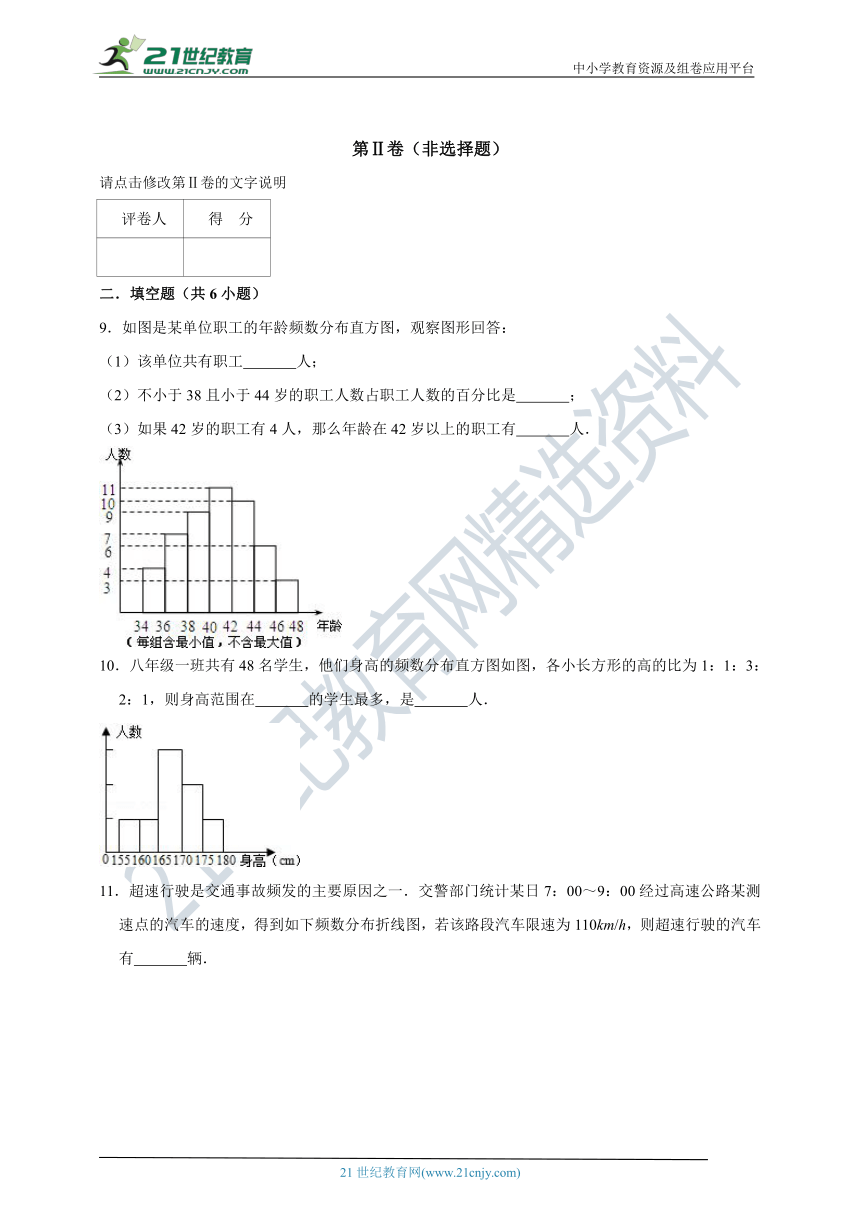
9．如图是某单位职工的年龄频数分布直方图，观察图形回答：
（1）该单位共有职工　 　人；
（2）不小于38且小于44岁的职工人数占职工人数的百分比是　 　；
（3）如果42岁的职工有4人，那么年龄在42岁以上的职工有　 　人．

10．八年级一班共有48名学生，他们身高的频数分布直方图如图，各小长方形的高的比为1：1：3：2：1，则身高范围在　 　的学生最多，是　 　人．

11．超速行驶是交通事故频发的主要原因之一．交警部门统计某日7：00～9：00经过高速公路某测速点的汽车的速度，得到如下频数分布折线图，若该路段汽车限速为110km/h，则超速行驶的汽车有　 　辆．

12．某班60名学生的期末成绩（成绩为整数）的频数分布表如下，请根据表中提供的信息回答下列问题：
分组 频数 频率
49.5﹣59.5 3 0.05
59.5﹣69.5 9 m
69.5﹣79.5 0.40
79.5﹣89.5 18 0.30
89.5﹣99.5 6 0.10
合计 60 1.00
（1）成绩在69.5～79.5范围内的频数是　 　；
（2）频率m＝　 　；
（3）在表中，频率最小的一组成绩的范围是　 　；
（4）成绩优秀的学生有　 　人（成绩大于或等于80分为优秀）．
13．某中学在一次健康知道竞赛活动中，抽取了一部分同学测试的成绩，绘制的成绩统计图如图所示，请结合统计图回答下列问题：
（1）本次测试中，抽取了的学生有　 　人；
（2）若这次测试成绩80分以上（含80分）为优秀，则请你估计这次测试成绩的优秀率不低于　 　%．
14．某校八年级（1）班为了了解同学们一天零花钱的消费情况，对本班同学开展了调查，将同学一天的零花钱以2元为组距，绘制如图的频率分布直方图，已知从左到右各组的频数之比为2：3：4：2：1．
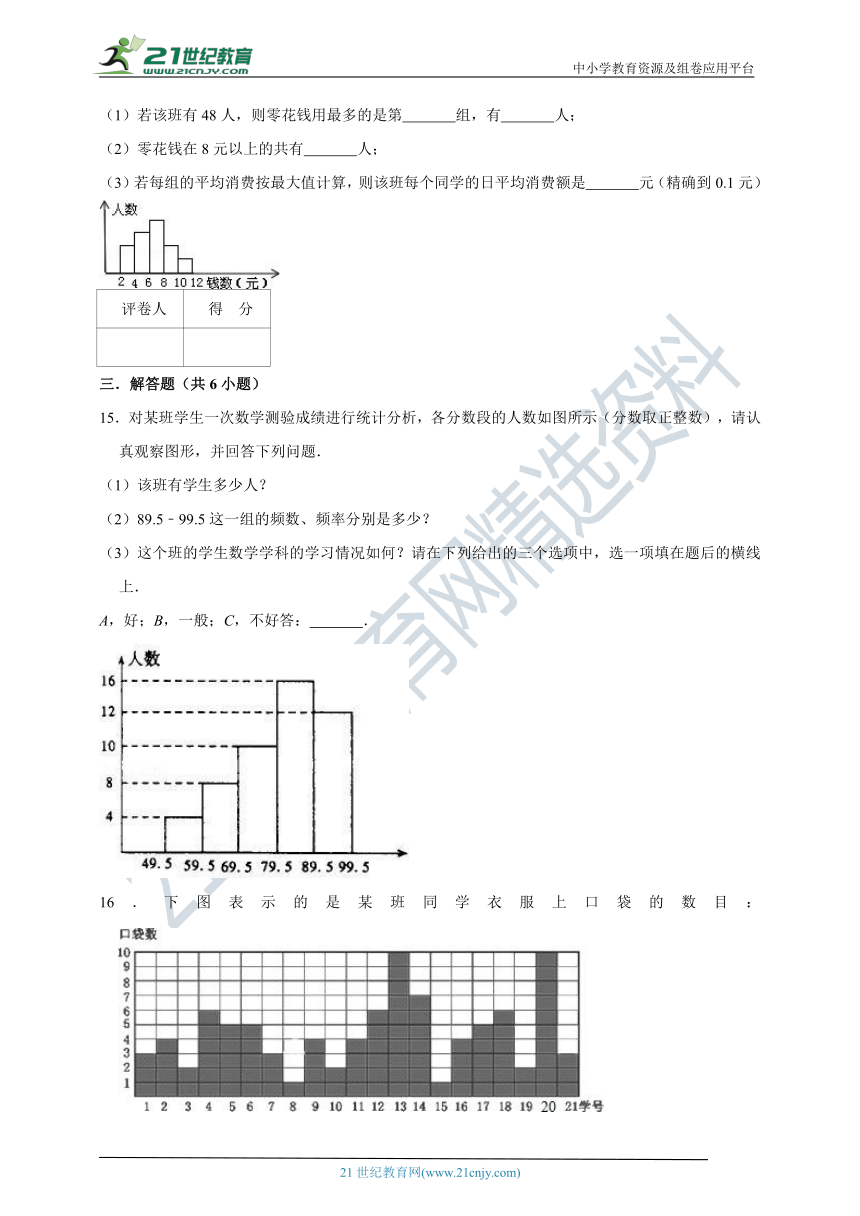
（1）若该班有48人，则零花钱用最多的是第　 　组，有　 　人；
（2）零花钱在8元以上的共有　 　人；
（3）若每组的平均消费按最大值计算，则该班每个同学的日平均消费额是　 　元（精确到0.1元）

评卷人 得 分

三．解答题（共6小题）
15．对某班学生一次数学测验成绩进行统计分析，各分数段的人数如图所示（分数取正整数），请认真观察图形，并回答下列问题．
（1）该班有学生多少人？
（2）89.5﹣99.5这一组的频数、频率分别是多少？
（3）这个班的学生数学学科的学习情况如何？请在下列给出的三个选项中，选一项填在题后的横线上．
A，好；B，一般；C，不好答：　 　．

16．下图表示的是某班同学衣服上口袋的数目：
（1）从图中是否能够得出以下信息：
①只有4个人的衣服上有4个口袋；
②只有1个人的衣服上有8个口袋；
③只有3个人的衣服上有5个口袋；
（2）根据上图填写下面的频数分布表，并绘制频数分布直方图．
口袋数目 1≤x＜3 3≤x＜5 5≤x＜7 7≤x＜9 x≥9
频数记录
频 数
17．七年级教师对试卷讲评课中学生参与的深度与广度进行评价调查，其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项．评价组随机抽取了若干名初中学生的参与情况，绘制成如图所示的频数分布直方图和扇形统计图（均不完整），请根据图中所给信息解答下列问题：

（1）在这次评价中，一共抽查了　 　名学生，“独立思考”人数占总人数的　 　%；
（2）求扇形统计图中，项目“主动质疑”所在的扇形的圆心角的度数；
（3）请将条形统计图补充完整．
18．某校组织1000名学生参加“青少年普法知识大赛”，为了了解学生的参赛成绩，从中抽取部分学生的参赛成绩（成绩均为整数）进行统计，并绘制成如下的不完全统计图表．
组别 分数段 频数 频率
一 50.5﹣60.5 16 0.08
二 60.5﹣70.5 30 0.15
三 70.5﹣80.5 50 0.25
四 80.5﹣90.5 m 0.40
五 90.5﹣100.5 24 n
请根据所给信息，解答下列问题：
（1）表中m＝　 　，n＝　 　；
（2）补全频数分布直方图；
（3）若成绩超过80分为优秀，分别求出被抽取的学生中优秀的学生频数和频率．

19．为增强学生的身体素质，教育行政部门规定学生每天户外活动的平均时间少于1小时，为了解学生参加户外活动的情况，对部分学生参加户外活动的时间进行抽样调查，并将调查结果绘制成如图所示中两幅不完整的统计图，请你根据图中提供的信息解答下列问题：

（1）在这次调查中共调查了多少名学生？
（2）求户外活动时间为0.5小时的人数，并补充频数分布直方图；
（3）求表示户外活动时间为2小时的扇形圆心角的度数．
20．解答题．
某校学生积极为地震灾区捐款奉献爱心．小颖随机抽查其中30名学生的捐款情况如下：（单位：元）2、5、35、8、5、10、15、20、15、5、45、10、2、8、20、30、40、10、15、15、30、15、8、25、25、30、15、8、10、50．
（1）这30名学生捐款的最大值、最小值、极差、平均数各是多少？
（2）将30名学生捐款额分成下面5组，请你完成频数统计表：
（3）根据上表，作出频数分布直方图．




参考答案与试题解析
一．选择题（共8小题）
1．如图，是某中学九（3）班学生外出方式（乘车、步行、骑车）的不完整频数（人数）分布直方图．如果乘车的频率是0.4，那么步行的频率为（　　）

A．0.4 B．0.36 C．0.3 D．0.24
【分析】根据乘车的人数和频率，求出总人数，再根据直方图给出的数据求出步行的人数，从而得出步行的频率．
【解答】解：∵乘车的有20人，它的频率是0.4，
∴总人数是＝50人，
∴步行的频率为＝0.36；
故选：B．
【点评】此题考查了频数（率）分布直方图，利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．
2．如图是某班45名同学爱心捐款额的频数分布直方图（每组含前一个边界值，不含后一个边界值），则捐款人数最多的一组是（　　）

A．5～10元 B．10～15元 C．15～20元 D．20～25元
【分析】根据图形所给出的数据直接找出捐款人数最多的一组即可．
【解答】解：根据图形所给出的数据可得：
捐款额为15～20元的有20人，人数最多，
则捐款人数最多的一组是15﹣20元．
故选：C．
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．
3．一个容量为80的样本最大值为143，最小值为50，取组距为10，则可以分成（　　）
A．10组 B．9组 C．8组 D．7组
【分析】根据组数＝（最大值﹣最小值）÷组距计算，注意小数部分要进位．
【解答】解：在样本数据中最大值为143，最小值为50，它们的差是143﹣50＝93，已知组距为10，那么由于＝，故可以分成10组．
故选：A．
【点评】本题考查的是组数的计算，属于基础题，只要根据组数的定义“数据分成的组的个数称为组数”来解即可．
4．某校初中三年级共有学生400人，为了解这些学生的视力情况，抽查了20名学生的视力，对所得数据进行整理，在得到的频数分布表中，若数据在0.95～1.15这一小组的频率为0.3，则可估计该校初中三年级学生视力在0.95～1.15范围内的人数约为（　　）
A．6人 B．30人 C．60人 D．120人
【分析】解答此题，应该利用公式：频率＝进行计算．已知了0.95～1.15这一小组的频率，关键是确定数据总和，题目求的是“初中三年级学生”视力在0.95～1.15范围内的人数，显然，初中三年级的总人数应该是数据总和，代值计算即可．
【解答】解：根据题意可得：共有学生400人且数据在0.95～1.15这一小组的频率为0.3，
那么在此范围的人数是400×0.3＝120（人）．
故选：D．
【点评】此题考查频率、频数的关系为频率＝．
5．为了了解某校七年级学生的体能情况，随机调查了其中100名学生，测试学生在1分钟内跳绳的次数，并绘制成如图所示的频数分布直方图．请根据图形计算，跳绳次数（x）在120≤x＜200范围内人数占抽查学生总人数的百分比为（　　）

A．43% B．50% C．57% D．73%
【分析】用120≤x＜200范围内人数除以总人数即可．
【解答】解：总人数为10+33+40+17＝100人，
120≤x＜200范围内人数为40+17＝57人，
在120≤x＜200范围内人数占抽查学生总人数的百分比为＝57%．
故选：C．
【点评】本题考查了频数分布直方图，把图分析透彻是解题的关键．
6．某校七（3）班的同学进行了一次安全知识测试，测试成绩进行整理后分成四个组，并绘制如图所示的频数直方图，则第二组的频数是（　　）

A．0.4 B．18 C．0.6 D．27
【分析】根据频数分布直方图即可求解．
【解答】解：根据频数分布直方图可知，第二组的频数是18．
故选：B．

【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．
7．频数分布直方图的纵轴表示（　　）
A． B． C． D．
【分析】根据频率分布直方图中纵横坐标的意义即可得．
【解答】解：频数分布直方图的纵轴表示，
故选：A．
【点评】本题考查频率直方图中横纵坐标表示的意义．
8．在频数分布直方图中，有11个小长方形，若中间一个小长方形的面积等于其它10个小长方形面积的和的，且数据有160个，则中间一组的频数为（　　）
A．32 B．0.2 C．40 D．0.25
【分析】频率分布直方图是用小长方形面积的大小来表示在各个区间内取值的频率．直角坐标系中的纵轴表示频率与组距的比值，即小长方形面积＝组距×频率在频数分布直方图中，计算出中间一个小长方形的面积占总面积的比值为＝，再由频率＝计算频数．
【解答】解：由于中间一个小长方形的面积等于其它10个小长方形面积的和的，
则中间一个小长方形的面积占总面积的＝，
即中间一组的频率为，且数据有160个，
∴中间一组的频数为＝32．
故选：A．
【点评】本题考查分析频数分布直方图和频率的求法．解本题要懂得频率分布直分图的意义，了解频率分布直分图是一种以频数为纵向指标的条形统计图．
二．填空题（共6小题）
9．如图是某单位职工的年龄频数分布直方图，观察图形回答：
（1）该单位共有职工　50　人；
（2）不小于38且小于44岁的职工人数占职工人数的百分比是　60%　；
（3）如果42岁的职工有4人，那么年龄在42岁以上的职工有　15　人．

【分析】（1）根据人数总和即为该单位职工数计算；
（2）根据不小于38岁但小于44岁的职工人数÷总人数＝占总人数的百分比计算；
（3）根据42岁（含42岁）以上的职工数﹣42岁的职工数＝42岁以上的职工数计算．
【解答】解：（1）由直方图可知：该单位职工共有4+7+9+11+10+6+3＝50人；
（2）不小于38岁但小于44岁的职工人数为9+11+10＝30人，则占总人数的百分比为30÷50＝60%；
（3）42岁（含42岁）以上的职工有10+6+3＝19人，则42岁以上的职工有19﹣4＝15人．
故答案为：（1）50；（2）60%；（3）15．
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力．利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．
10．八年级一班共有48名学生，他们身高的频数分布直方图如图，各小长方形的高的比为1：1：3：2：1，则身高范围在　165cm～170cm　的学生最多，是　18　人．

【分析】根据各小长方形的高的比为1：1：3：2：1，所占比例最大的即是在这个身高范围内的学生最多，再利用高度之比也是人数之比，即可求出．
【解答】解：八年级一班共有48名学生，他们身高的频数分布直方图如图，各小长方形的高的比为1：1：3：2：1，
∴最高的即表示在这个身高范围内的学生最多，
∴165cm～170cm这个身高范围内的学生最多，
这个身高范围内的学生有：48×＝18人．
故答案为：165cm～170cm，18．
【点评】此题考查了利用频数分布直方图中小矩形的高度之比与频数的关系，主要训练利用统计图获取信息的能力，利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．
11．超速行驶是交通事故频发的主要原因之一．交警部门统计某日7：00～9：00经过高速公路某测速点的汽车的速度，得到如下频数分布折线图，若该路段汽车限速为110km/h，则超速行驶的汽车有　80　辆．

【分析】根据图中的信息，找到符合条件的数据，再进一步计算．
【解答】解：读图可知：
超过限速110km/h的有60+20＝80（辆）．
故答案为：80．
【点评】本题考查读频数分布折线图的能力和利用统计图获取信息的能力．
利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．
12．某班60名学生的期末成绩（成绩为整数）的频数分布表如下，请根据表中提供的信息回答下列问题：
分组 频数 频率
49.5﹣59.5 3 0.05
59.5﹣69.5 9 m
69.5﹣79.5 0.40
79.5﹣89.5 18 0.30
89.5﹣99.5 6 0.10
合计 60 1.00
（1）成绩在69.5～79.5范围内的频数是　24　；
（2）频率m＝　0.15　；
（3）在表中，频率最小的一组成绩的范围是　49.5﹣59.5　；
（4）成绩优秀的学生有　24　人（成绩大于或等于80分为优秀）．
【分析】（1）由合计总数减去其他范围中的频数即可求出成绩在69.5～79.5范围内的频数；
（2）由1减去其他范围中的频率即可求出m的值；
（3）观察表格，得出频率最小的成绩范围即可；
（4）求出成绩在79.5﹣89.5及89.5﹣99.5的频率之和，乘以24即可得到结果．
【解答】解：（1）根据题意得：60﹣（3+9+18+6）＝24，
则成绩在69.5～79.5范围内的频数是24；

（2）根据题意得：1﹣（0.05+0.40+0.30+0.10）＝0.15，
则m＝0.15；

（3）观察表格得：频率最小的一组成绩的范围是49.5﹣59.5；

（4）根据题意得：60×（0.30+0.10）＝24（人），
则成绩优秀的学生有24人．
故答案为：（1）24；（2）0.15；（3）49.5﹣59.5；（4）24．
【点评】此题考查了频数（率）分布表，弄清题意是解本题的关键．
13．某中学在一次健康知道竞赛活动中，抽取了一部分同学测试的成绩，绘制的成绩统计图如图所示，请结合统计图回答下列问题：
（1）本次测试中，抽取了的学生有　50　人；
（2）若这次测试成绩80分以上（含80分）为优秀，则请你估计这次测试成绩的优秀率不低于　90　%．
【分析】（1）由频数直方图的意义，将各组人数相加可得共抽取的学生人数，即答案；
（2）读直方图可得：这次测试成绩80分以上的人数，除以总人数即可得优秀率，即答案．
【解答】解：（1）由频数直方图可知：本次测试中，抽取了的学生有2+3+41+4＝50人；

（2）这次测试成绩80分以上（含80分）的人数为41+4＝45，则优秀率为＝90%．
故答案为（1）50人；（2）90%．
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力．利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．
14．某校八年级（1）班为了了解同学们一天零花钱的消费情况，对本班同学开展了调查，将同学一天的零花钱以2元为组距，绘制如图的频率分布直方图，已知从左到右各组的频数之比为2：3：4：2：1．
（1）若该班有48人，则零花钱用最多的是第　3　组，有　16　人；
（2）零花钱在8元以上的共有　12　人；
（3）若每组的平均消费按最大值计算，则该班每个同学的日平均消费额是　7.5　元（精确到0.1元）

【分析】（1）根据频数分布直方图的特点可知，小正方形越高，数值越大，反之越小，据此解答即可．
（2）根据频数＝总人数×频率计算即可．
（3）计算出各组的人数，然后根据平均数的定义即可求解．
【解答】解：（1）由图可知，零花钱用最多的是第3组，有48×＝16人；

（2）8元以上的频率＝＝，
∴零花钱在8元以上的人数为：48×＝12．

（3）平均数＝＝7.5．
故答案为：3，16，12，7.5．
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力．利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．
三．解答题（共6小题）
15．对某班学生一次数学测验成绩进行统计分析，各分数段的人数如图所示（分数取正整数），请认真观察图形，并回答下列问题．
（1）该班有学生多少人？
（2）89.5﹣99.5这一组的频数、频率分别是多少？
（3）这个班的学生数学学科的学习情况如何？请在下列给出的三个选项中，选一项填在题后的横线上．
A，好；B，一般；C，不好答：　A　．

【分析】（1）各分数段的人数和就是总人数．
（2）89.5﹣99.5这一组的频率等于该组的频数除以总频数．
（3）计算一下该班的及格率与优秀率，然后判断该班学生数学学科的学习情况．
【解答】解：（1）4+8+10+12+16＝50；
（2）由图知89.5﹣99.5这一组的频数是12，频率为：12÷50＝0.24；
（3）该班的及格率为：（8+10+12+16）÷50＝92%，该班的优秀率为（16+12）÷50＝56%．
该班的及格率、优秀率都很高．
故选A．
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力，同时考查了同学们的判断能力．
16．下图表示的是某班同学衣服上口袋的数目：
（1）从图中是否能够得出以下信息：
①只有4个人的衣服上有4个口袋；
②只有1个人的衣服上有8个口袋；
③只有3个人的衣服上有5个口袋；
（2）根据上图填写下面的频数分布表，并绘制频数分布直方图．
口袋数目 1≤x＜3 3≤x＜5 5≤x＜7 7≤x＜9 x≥9
频数记录
频 数
【分析】（1）由图可以看出：有4个口袋的人为4人，有8个口袋的人数为0人，有5个口袋的人数为3人，则①③是正确的；
（2）直接根据（1）得出的数据填表作图即可．
【解答】解：
（1）能得到①③；

（2）
口袋数目 1≤x＜3 3≤x＜5 5≤x＜7 7≤x＜9 x≥9
频数记录
频 数 5 7 6 1 2

【点评】本题是考查同学们列频数分布表、画直方图的能力．
17．七年级教师对试卷讲评课中学生参与的深度与广度进行评价调查，其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项．评价组随机抽取了若干名初中学生的参与情况，绘制成如图所示的频数分布直方图和扇形统计图（均不完整），请根据图中所给信息解答下列问题：

（1）在这次评价中，一共抽查了　560　名学生，“独立思考”人数占总人数的　30　%；
（2）求扇形统计图中，项目“主动质疑”所在的扇形的圆心角的度数；
（3）请将条形统计图补充完整．
【分析】（1）根据专注听讲的人数是224人，所占的比例是40%，即可求得抽查的总人数，用“独立思考”人数除以总人数可得其百分比；
（2）利用360°乘以对应的百分比即可求解；
（3）利用总人数减去其他各组的人数，即可求得讲解题目的人数，从而作出频数分布直方图．
【解答】解：（1）调查的总人数是：224÷40%＝560（人），
“独立思考”人数占总人数的百分比为×100%＝30%，
故答案是：560、30；

（2）“主动质疑”所在的扇形的圆心角的度数是：360°×＝54°；

（3）“讲解题目”的人数是：560﹣84﹣168﹣224＝84（人）．

【点评】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
18．某校组织1000名学生参加“青少年普法知识大赛”，为了了解学生的参赛成绩，从中抽取部分学生的参赛成绩（成绩均为整数）进行统计，并绘制成如下的不完全统计图表．
组别 分数段 频数 频率
一 50.5﹣60.5 16 0.08
二 60.5﹣70.5 30 0.15
三 70.5﹣80.5 50 0.25
四 80.5﹣90.5 m 0.40
五 90.5﹣100.5 24 n
请根据所给信息，解答下列问题：
（1）表中m＝　80　，n＝　0.12　；
（2）补全频数分布直方图；
（3）若成绩超过80分为优秀，分别求出被抽取的学生中优秀的学生频数和频率．

【分析】（1）先根据第1组的频数及其频率求得被抽查的总人数，再根据“频率＝频数÷总数”可分别求得m、n的值；
（2）根据（1）中m的值即可补全图形；
（3）将第四、五组的频数、频率分别相加即可得．
【解答】解：（1）∵调查的总人数为16÷0.08＝200，
∴m＝200×0.4＝80，n＝24÷200＝0.12，
故答案为：80、0.12；

（2）


（3）被抽取的学生中优秀的学生频数为80+24＝104，频率为0.40+0.12＝0.52．
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题，本题的关键在于根据频数分布表与频数分布直方图得到56.5～60.5一组的信息，然后求出被抽查的学生的人数．
19．为增强学生的身体素质，教育行政部门规定学生每天户外活动的平均时间少于1小时，为了解学生参加户外活动的情况，对部分学生参加户外活动的时间进行抽样调查，并将调查结果绘制成如图所示中两幅不完整的统计图，请你根据图中提供的信息解答下列问题：

（1）在这次调查中共调查了多少名学生？
（2）求户外活动时间为0.5小时的人数，并补充频数分布直方图；
（3）求表示户外活动时间为2小时的扇形圆心角的度数．
【分析】（1）根据时间是1小时的有32人，占40%，据此即可求得总人数；
（2）利用总人数乘以百分比即可求得时间是0.5小时的一组的人数，即可作出直方图；
（3）利用360°乘以活动时间是2小时的一组所占的百分比即可求得圆心角的度数．
【解答】解：（1）调查人数＝32÷40%＝80（人）；
（2）户外活动时间为0.5小时的人数＝80×20%＝16（人）；
补全频数分布直方图见下图：

（3）表示户外活动时间2小时的扇形圆心角的度数＝×360°＝54°．
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．
20．解答题．
某校学生积极为地震灾区捐款奉献爱心．小颖随机抽查其中30名学生的捐款情况如下：（单位：元）2、5、35、8、5、10、15、20、15、5、45、10、2、8、20、30、40、10、15、15、30、15、8、25、25、30、15、8、10、50．
（1）这30名学生捐款的最大值、最小值、极差、平均数各是多少？
（2）将30名学生捐款额分成下面5组，请你完成频数统计表：
（3）根据上表，作出频数分布直方图．

【分析】（1）根据给出的数据以及极差、平均数的计算方法直接计算即可解答．
（2）分别找出各组的人数填表即可解答．
（3）根据频数分布表画出频数分布直方图即可解答．
【解答】解：（1）这30名学生捐款的最大值为50，
最小值为2，
极差为50﹣2＝48，
平均数为（2+5+35+8+5+10+15+20+15+5+45+10+2+8+20+30+40+10+15+15+30+15+8+25+25+30+15+8+10+50）÷30＝17.7元．

（2）填表如下：
．
（3）画图如下：

【点评】本题主要考查极差、平均数的定义以及画频数分布直方图的能力，正确画图是关键．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布
日期：2019/2/1 21:09:54；用户：zhrasce20；邮箱：zhrasce20@163.com；学号：6322261
























21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）



HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)