1.4 平行线的性质同步练习(含解析)
文档属性
| 名称 | 1.4 平行线的性质同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 227.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-17 09:57:06 | ||
图片预览



文档简介
1.4平行线的性质 同步练习
一、单选题
1.如图,直线 ,直线l与直线a,b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若 ,则 的度数为(?? )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
2.如图,AD∥BC,∠C=30°,∠ADB:∠BDC=1:2,则∠DBC的度数是(?? )
A.?30°???????????????????????????????????????B.?36°???????????????????????????????????????C.?45°???????????????????????????????????????D.?50°
3.如图,直线l1∥l2 ,且分别与直线l交于C,D两点,把一块含30°角的三角尺按如图所示的位置摆放.若∠1=52°,则∠2的度数为(???? )
A.?92°?????????????????????????????????????B.?98°?????????????????????????????????????C.?102°?????????????????????????????????????D.?108°
4.如图,快艇从P处向正北航行到A处时,向左转50°航行到B处,再向右转80°继续航行,此时的航行方向为(?? )
A.?北偏东30°?????????????????????????B.?北偏东80°?????????????????????????C.?北偏西30°?????????????????????????D.?北偏西50°
5.如图,直线AB∥EF,点C是直线AB上一点,点D是直线AB外一点,若∠BCD=95°,∠CDE=25°,则∠DEF的度数是(?? )
A.?110°????????????????????????????????????B.?115°????????????????????????????????????C.?120°????????????????????????????????????D.?125°
6.如图,BE平分∠DBC,点A是BD上一点,过点A作AE∥BC交BE于点E,∠DAE=56°,则∠E的度数为(?? )
A.?56°???????????????????????????????????????B.?36°???????????????????????????????????????C.?26°???????????????????????????????????????D.?28°
7.如图,AB∥CD,则图中α,β,γ三者之间的关系是(?? )
A.?α+β+γ=180°??????????????????B.?α–β+γ=180°??????????????????C.?α+β–γ=180°??????????????????D.?α+β+γ=360°
8.如图, ,下列结论: ; ; ; ,其中正确的结论有(?? )
A.?????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?
二、填空题
9.如图,A.B之间是一座山,一条铁路要通过A.B两地,在A地测得B地在北偏东70°,如果A.B两地同时开工修建铁路,那么在B地应按________方向开凿,才能使铁路在山腹中准确接通.
10.如图,AB∥CD,CB平分∠ACD.若∠BCD=28°,则∠A的度数为________.
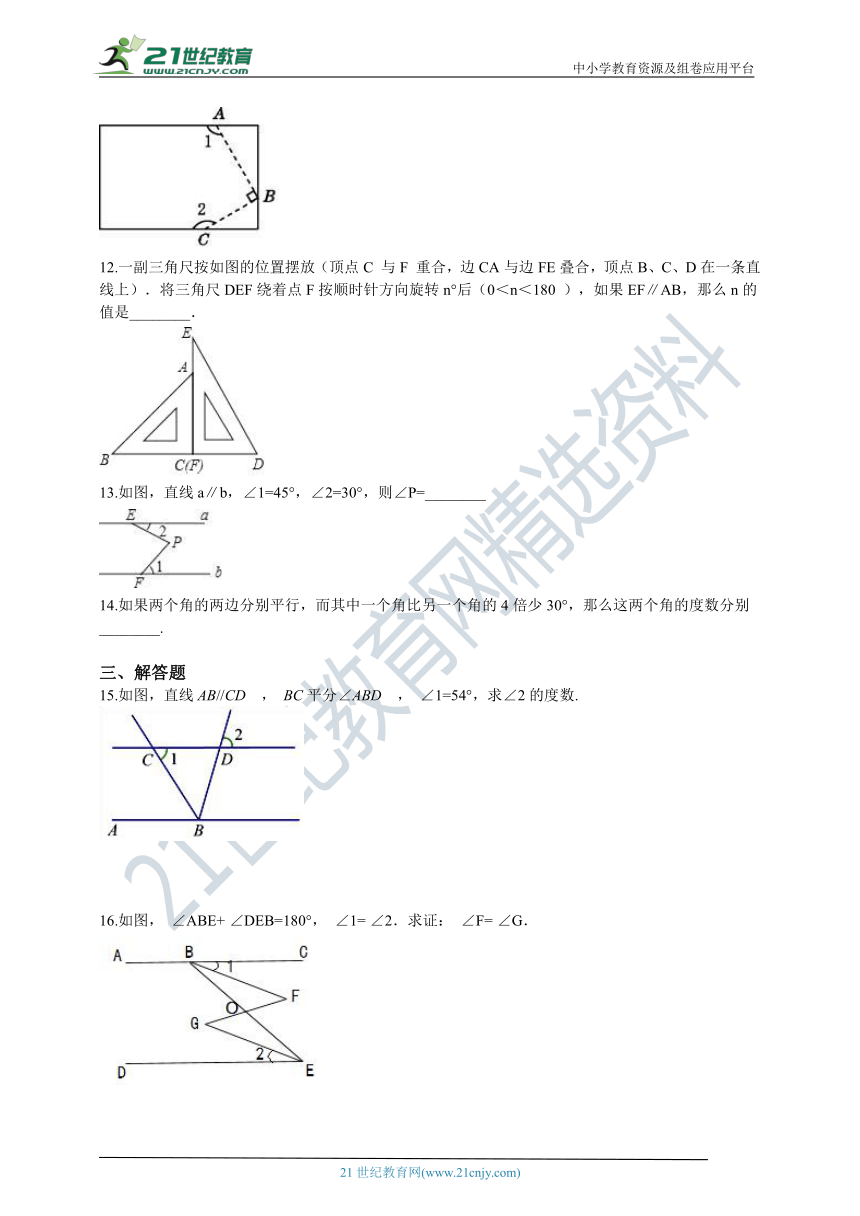
11.如图,若按虚线剪去长方形纸片相邻的两个角,并使∠1=120°,则∠2的度数为________
12.一副三角尺按如图的位置摆放(顶点C 与F 重合,边CA与边FE叠合,顶点B、C、D在一条直线上).将三角尺DEF绕着点F按顺时针方向旋转n°后(0<n<180 ),如果EF∥AB,那么n的值是________.
13.如图,直线a∥b,∠1=45°,∠2=30°,则∠P=________
14.如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角的度数分别________.
三、解答题
15.如图,直线AB//CD , BC平分∠ABD , ∠1=54°,求∠2的度数.
16.如图, ∠ABE+ ∠DEB=180°, ∠1= ∠2.求证: ∠F= ∠G.
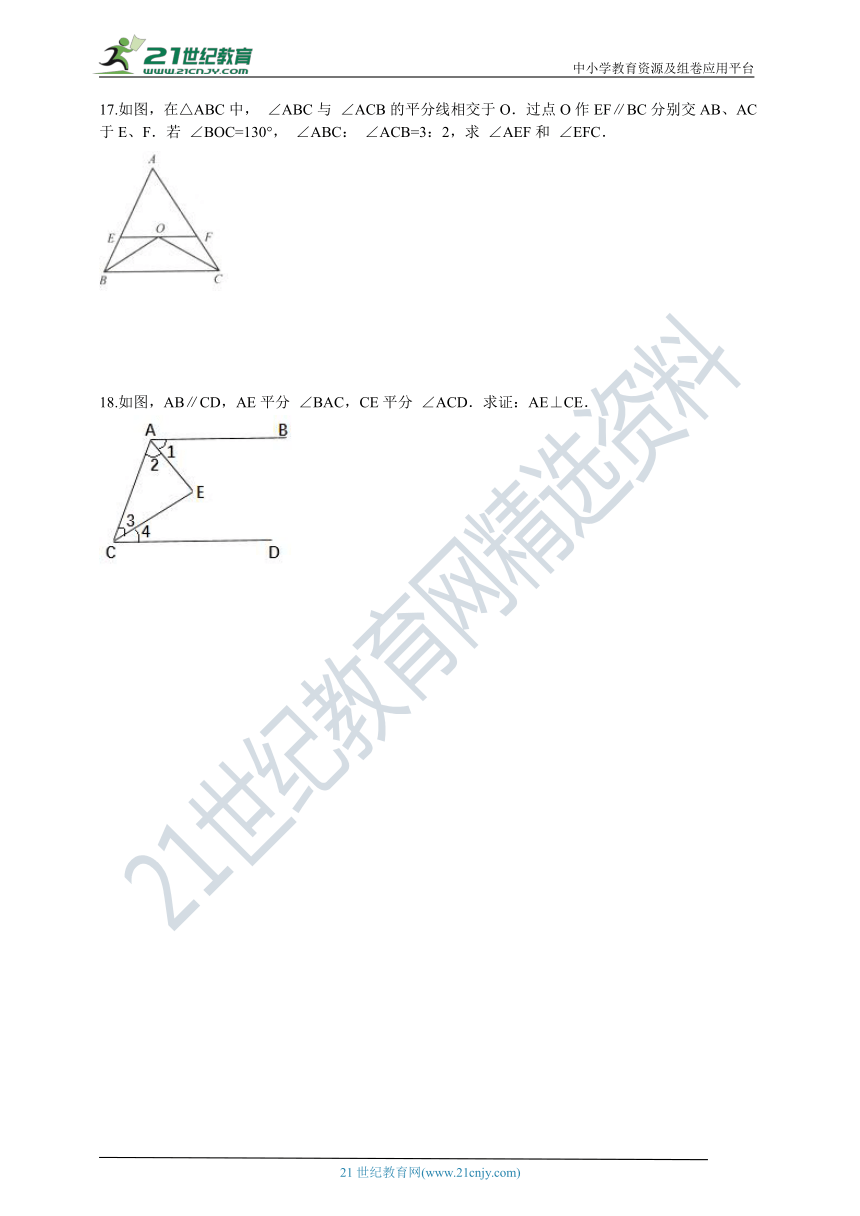
17.如图,在△ABC中, ∠ABC与 ∠ACB的平分线相交于O.过点O作EF∥BC分别交AB、AC于E、F.若 ∠BOC=130°, ∠ABC: ∠ACB=3:2,求 ∠AEF和 ∠EFC.
18.如图,AB∥CD,AE平分 ∠BAC,CE平分 ∠ACD.求证:AE⊥CE.
参考答案与试题解析
一、单选题
1.解:∵AC⊥BA,
∴∠BAC=90°,
∴∠ACB=90°-∠1=90°-58°=32°,
∵直线a∥b,
∴∠ACB=∠2,
∴∠2=∠ACB=32°.
故答案为:C.
2.解:∵AD∥BC,∠C=30°,
∴∠ADC=150°,∠ADB=∠DBC,
∵∠ADB:∠BDC=1:2,
∴∠ADB=×150°=50°,
∴∠DBC的度数是50°.
故答案为:D.
3.解:如图,
∵l1∥l2 ,
∴∠1=∠3=52°,
又∵∠4=30°,
∴∠2=180°-∠3-∠4=98°.
故答案为:B.
4.解:如图,
AP∥BC,
∴∠2=∠1=50°,
∵∠EBF=80°=∠2+∠3,
∴∠3=∠EBF﹣∠2=80°﹣50°=30°,
∴此时的航行方向为北偏东30°,
故答案为:A.
5.解:延长FE交DC于点N,
∵直线AB∥EF,
∴∠DNF=∠BCD =95°,
∵∠CDE=25°,
∴∠DEF=95°+25°=120°.
故答案为:C.
6.解:∵AE∥BC,∠DAE=56°,
∴∠DBC=56°,∠E=∠EBC,
∵BE平分∠DBC,
∴∠EBC=∠DBC=28°,
∴∠E=28°,
故答案为:D.
7.解:如图,延长AE交直线CD于F,
∵AB∥CCD,
∵∠AFD=∠β?∠γ,
故答案为:C.
8.解:因为∠B=∠C,所以AB∥CD,∠A=∠AEC,因为∠A=∠D,所以∠AEC=∠D,所以AE∥DF,∠AMC=∠FNC,因为∠BND=∠FNC,所以∠AMC=∠BND,无法得到AE⊥BC,所以正确的结论有①②④,故答案为:A.
二、填空题
9.解:
∵AE∥BF,
∴∠1=∠A=70°,
即在B点应按南偏西70°方向开凿,才能使铁路在山腹中准确接通,
故答案为:南偏西70°
10.解:根据平行线的性质得到∠ABC=∠BCD=28°,根据角平分线的定义得到∠ACB=∠BCD=28°,根据三角形的内角和即可得到∠A=180°﹣∠ABC﹣∠ACB=124°, 故答案为:124°.
11.解:过点B作BD∥CE ∴∠2+∠4=180° ∵AF∥CE ∴AF∥BD ∴∠1+∠3=180° ∴∠3=180°-120°=60° ∵∠3+∠4=90° ∴∠4=90°-60°=30° ∴∠2=180°-∠4=180°-30°=150° 故答案为:150°
12.解:①如图1中,
EF∥AB时,∠ACE=∠A=45°,∴旋转角n=45时,EF∥AB.
②如图2中,
EF∥AB时,∠ACE+∠A=180°,∴∠ACE=135°
∴旋转角n=360°﹣135°=225°,∵0<n°<180,∴此种情形不合题意,故答案为:45.
解:过P作PM∥直线a, ∵直线a∥b, ∴直线a∥b∥PM, ∵∠1=45°,∠2=30°, ∴∠EPM=∠2=30°,∠FPM=∠1=45°, ∴∠EPF=∠EPM+∠FPM=30°+45°=75°, 故答案为:75
14.解:设另一个角为α,则这个角是4α﹣30°, ∵两个角的两边分别平行, ∴α+4α﹣30°=180°或α=4α﹣30°, 解得α=42°或α=10°, ∴4α﹣30°=138°或4α﹣30°=10°, 这两个角是42°,138°或10°,10°. 故答案为:42°,138°或10°,10°.
三、解答题
15.解:根据二直线平行,内错角相等得出∠ABC=∠1=54°,
根据角平分线的定义得出∠ABD=2∠ABC =2×54°=108°,
根据二直线平行同旁内角互补得出∠CDB=180°-∠ABD=72°,
根据对顶角相等得出答案。
解:根据平行线的判定得AC∥DE,
再由平行线的性质内错角∠CBO=∠DEO,
结合已知条件得∠FBO=∠GEO,
在△BFO和△GEO中,
由三角形内角和定理即可得证.
解:根据已知条件设∠ABC=3x, ∠ACB=2x,
由角平分线性质得∠ABO=∠CBO=x,∠ACO=∠BCO=x,
在△BOC中,根据三角形内角和定理列出方程,
解之求得x值,从而得∠ABC=60°, ∠ACB=40°,
再由平行线性质同位角相等得∠AEF=60°,
同旁内角互补得∠EFC=140°.
解:由平行线性质可得∠BAC+∠ACD=180°;
再由角平分线性质可得∠2=?∠BAC, ∠3=∠ACD;
可得∠2+∠3=90°,
再由三角形内角和定理得∠E=90°,
即AE⊥CE.
一、单选题
1.如图,直线 ,直线l与直线a,b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若 ,则 的度数为(?? )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
2.如图,AD∥BC,∠C=30°,∠ADB:∠BDC=1:2,则∠DBC的度数是(?? )
A.?30°???????????????????????????????????????B.?36°???????????????????????????????????????C.?45°???????????????????????????????????????D.?50°
3.如图,直线l1∥l2 ,且分别与直线l交于C,D两点,把一块含30°角的三角尺按如图所示的位置摆放.若∠1=52°,则∠2的度数为(???? )
A.?92°?????????????????????????????????????B.?98°?????????????????????????????????????C.?102°?????????????????????????????????????D.?108°
4.如图,快艇从P处向正北航行到A处时,向左转50°航行到B处,再向右转80°继续航行,此时的航行方向为(?? )
A.?北偏东30°?????????????????????????B.?北偏东80°?????????????????????????C.?北偏西30°?????????????????????????D.?北偏西50°
5.如图,直线AB∥EF,点C是直线AB上一点,点D是直线AB外一点,若∠BCD=95°,∠CDE=25°,则∠DEF的度数是(?? )
A.?110°????????????????????????????????????B.?115°????????????????????????????????????C.?120°????????????????????????????????????D.?125°
6.如图,BE平分∠DBC,点A是BD上一点,过点A作AE∥BC交BE于点E,∠DAE=56°,则∠E的度数为(?? )
A.?56°???????????????????????????????????????B.?36°???????????????????????????????????????C.?26°???????????????????????????????????????D.?28°
7.如图,AB∥CD,则图中α,β,γ三者之间的关系是(?? )
A.?α+β+γ=180°??????????????????B.?α–β+γ=180°??????????????????C.?α+β–γ=180°??????????????????D.?α+β+γ=360°
8.如图, ,下列结论: ; ; ; ,其中正确的结论有(?? )
A.?????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?
二、填空题
9.如图,A.B之间是一座山,一条铁路要通过A.B两地,在A地测得B地在北偏东70°,如果A.B两地同时开工修建铁路,那么在B地应按________方向开凿,才能使铁路在山腹中准确接通.
10.如图,AB∥CD,CB平分∠ACD.若∠BCD=28°,则∠A的度数为________.
11.如图,若按虚线剪去长方形纸片相邻的两个角,并使∠1=120°,则∠2的度数为________
12.一副三角尺按如图的位置摆放(顶点C 与F 重合,边CA与边FE叠合,顶点B、C、D在一条直线上).将三角尺DEF绕着点F按顺时针方向旋转n°后(0<n<180 ),如果EF∥AB,那么n的值是________.
13.如图,直线a∥b,∠1=45°,∠2=30°,则∠P=________
14.如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角的度数分别________.
三、解答题
15.如图,直线AB//CD , BC平分∠ABD , ∠1=54°,求∠2的度数.
16.如图, ∠ABE+ ∠DEB=180°, ∠1= ∠2.求证: ∠F= ∠G.
17.如图,在△ABC中, ∠ABC与 ∠ACB的平分线相交于O.过点O作EF∥BC分别交AB、AC于E、F.若 ∠BOC=130°, ∠ABC: ∠ACB=3:2,求 ∠AEF和 ∠EFC.
18.如图,AB∥CD,AE平分 ∠BAC,CE平分 ∠ACD.求证:AE⊥CE.
参考答案与试题解析
一、单选题
1.解:∵AC⊥BA,
∴∠BAC=90°,
∴∠ACB=90°-∠1=90°-58°=32°,
∵直线a∥b,
∴∠ACB=∠2,
∴∠2=∠ACB=32°.
故答案为:C.
2.解:∵AD∥BC,∠C=30°,
∴∠ADC=150°,∠ADB=∠DBC,
∵∠ADB:∠BDC=1:2,
∴∠ADB=×150°=50°,
∴∠DBC的度数是50°.
故答案为:D.
3.解:如图,
∵l1∥l2 ,
∴∠1=∠3=52°,
又∵∠4=30°,
∴∠2=180°-∠3-∠4=98°.
故答案为:B.
4.解:如图,
AP∥BC,
∴∠2=∠1=50°,
∵∠EBF=80°=∠2+∠3,
∴∠3=∠EBF﹣∠2=80°﹣50°=30°,
∴此时的航行方向为北偏东30°,
故答案为:A.
5.解:延长FE交DC于点N,
∵直线AB∥EF,
∴∠DNF=∠BCD =95°,
∵∠CDE=25°,
∴∠DEF=95°+25°=120°.
故答案为:C.
6.解:∵AE∥BC,∠DAE=56°,
∴∠DBC=56°,∠E=∠EBC,
∵BE平分∠DBC,
∴∠EBC=∠DBC=28°,
∴∠E=28°,
故答案为:D.
7.解:如图,延长AE交直线CD于F,
∵AB∥CCD,
∵∠AFD=∠β?∠γ,
故答案为:C.
8.解:因为∠B=∠C,所以AB∥CD,∠A=∠AEC,因为∠A=∠D,所以∠AEC=∠D,所以AE∥DF,∠AMC=∠FNC,因为∠BND=∠FNC,所以∠AMC=∠BND,无法得到AE⊥BC,所以正确的结论有①②④,故答案为:A.
二、填空题
9.解:
∵AE∥BF,
∴∠1=∠A=70°,
即在B点应按南偏西70°方向开凿,才能使铁路在山腹中准确接通,
故答案为:南偏西70°
10.解:根据平行线的性质得到∠ABC=∠BCD=28°,根据角平分线的定义得到∠ACB=∠BCD=28°,根据三角形的内角和即可得到∠A=180°﹣∠ABC﹣∠ACB=124°, 故答案为:124°.
11.解:过点B作BD∥CE ∴∠2+∠4=180° ∵AF∥CE ∴AF∥BD ∴∠1+∠3=180° ∴∠3=180°-120°=60° ∵∠3+∠4=90° ∴∠4=90°-60°=30° ∴∠2=180°-∠4=180°-30°=150° 故答案为:150°
12.解:①如图1中,
EF∥AB时,∠ACE=∠A=45°,∴旋转角n=45时,EF∥AB.
②如图2中,
EF∥AB时,∠ACE+∠A=180°,∴∠ACE=135°
∴旋转角n=360°﹣135°=225°,∵0<n°<180,∴此种情形不合题意,故答案为:45.
解:过P作PM∥直线a, ∵直线a∥b, ∴直线a∥b∥PM, ∵∠1=45°,∠2=30°, ∴∠EPM=∠2=30°,∠FPM=∠1=45°, ∴∠EPF=∠EPM+∠FPM=30°+45°=75°, 故答案为:75
14.解:设另一个角为α,则这个角是4α﹣30°, ∵两个角的两边分别平行, ∴α+4α﹣30°=180°或α=4α﹣30°, 解得α=42°或α=10°, ∴4α﹣30°=138°或4α﹣30°=10°, 这两个角是42°,138°或10°,10°. 故答案为:42°,138°或10°,10°.
三、解答题
15.解:根据二直线平行,内错角相等得出∠ABC=∠1=54°,
根据角平分线的定义得出∠ABD=2∠ABC =2×54°=108°,
根据二直线平行同旁内角互补得出∠CDB=180°-∠ABD=72°,
根据对顶角相等得出答案。
解:根据平行线的判定得AC∥DE,
再由平行线的性质内错角∠CBO=∠DEO,
结合已知条件得∠FBO=∠GEO,
在△BFO和△GEO中,
由三角形内角和定理即可得证.
解:根据已知条件设∠ABC=3x, ∠ACB=2x,
由角平分线性质得∠ABO=∠CBO=x,∠ACO=∠BCO=x,
在△BOC中,根据三角形内角和定理列出方程,
解之求得x值,从而得∠ABC=60°, ∠ACB=40°,
再由平行线性质同位角相等得∠AEF=60°,
同旁内角互补得∠EFC=140°.
解:由平行线性质可得∠BAC+∠ACD=180°;
再由角平分线性质可得∠2=?∠BAC, ∠3=∠ACD;
可得∠2+∠3=90°,
再由三角形内角和定理得∠E=90°,
即AE⊥CE.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
