1.5 图形的平移同步练习（含解析）

1.5图形的平移 同步练习
一、单选题
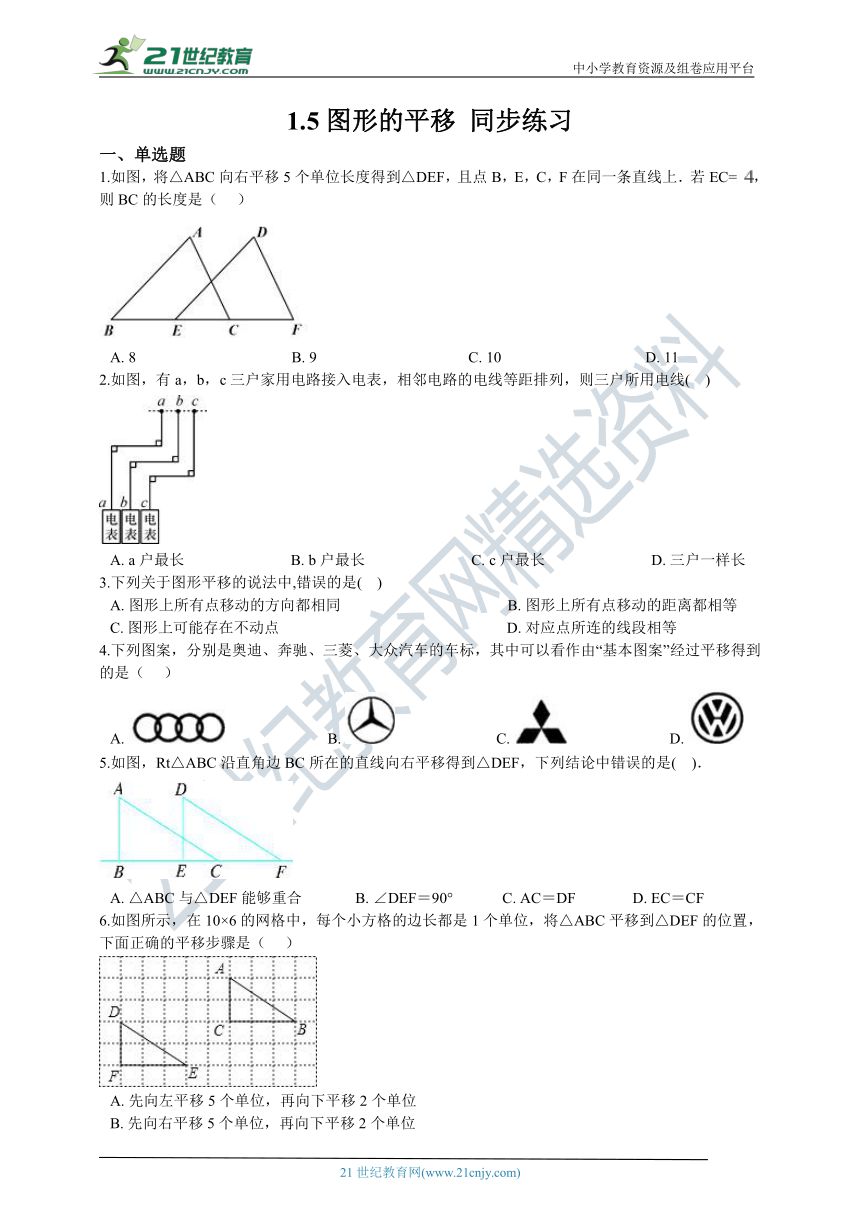
1.如图，将△ABC向右平移5个单位长度得到△DEF，且点B，E，C，F在同一条直线上．若EC= ，则BC的长度是（? ??）
A.?8???????????????????????????????????????B.?9???????????????????????????????????????C.?10???????????????????????????????????????D.?11
2.如图，有a，b，c三户家用电路接入电表，相邻电路的电线等距排列，则三户所用电线(? ?)
A.?a户最长????????????????????????????B.?b户最长????????????????????????????C.?c户最长????????????????????????????D.?三户一样长
3.下列关于图形平移的说法中,错误的是(?? )
A.?图形上所有点移动的方向都相同 B.?图形上所有点移动的距离都相等C.?图形上可能存在不动点 D.?对应点所连的线段相等
4.下列图案，分别是奥迪、奔驰、三菱、大众汽车的车标，其中可以看作由“基本图案”经过平移得到的是（ ???）
A.????????????????????????????B.????????????????????????????C.????????????????????????????D.?
5.如图，Rt△ABC沿直角边BC所在的直线向右平移得到△DEF，下列结论中错误的是(?? )．
A.?△ABC与△DEF能够重合??????????????B.?∠DEF＝90°?????????????C.?AC＝DF???????????????D.?EC＝CF
6.如图所示，在10×6的网格中，每个小方格的边长都是1个单位，将△ABC平移到△DEF的位置，下面正确的平移步骤是（??? ）
A.?先向左平移5个单位，再向下平移2个单位B.?先向右平移5个单位，再向下平移2个单位C.?先向左平移5个单位，再向上平移2个单位D.?先向右平移5个单位，再向上平移2个单位
7.如图：O是正六边形ABCDEF的中心，下列图形中可由△OB C平移得到的是（??? ）
A.?△OCD??????????????????????????????B.?△OAB??????????????????????????????C.?△OAF??????????????????????????????D.?以上都不对
8.判断下列现象中是平移的有几种？(?? )．
( 1 )篮球运动员投出篮球的运动；(2)升降机上上下下运送东西；(3)空中放飞的风筝的运动；(4)飞机在跑道上滑行到停止的运动；(5)铝合金窗叶左右平移；(6)电脑的风叶的运动．
A.?2种???????????????????????????????????????B.?3种???????????????????????????????????????C.?4种???????????????????????????????????????D.?5种
二、填空题
9.如图,将三角形ABC沿直线AB的方向向右平移至三角形BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为________
10.如图，在Rt△ABC中，∠C=90°，AC=4，将△ABC沿CB向右平移得到△DEF，若平移距离为2，则四边形ABED的面积等于________．
11.如图，△ABC中，AB=AC，BC=12cm，点D在AC上，DC=4cm．将线段DC沿着CB的方向平移7cm得到线段EF，点E，F分别落在边AB，BC上，则△EBF的周长为________?cm．

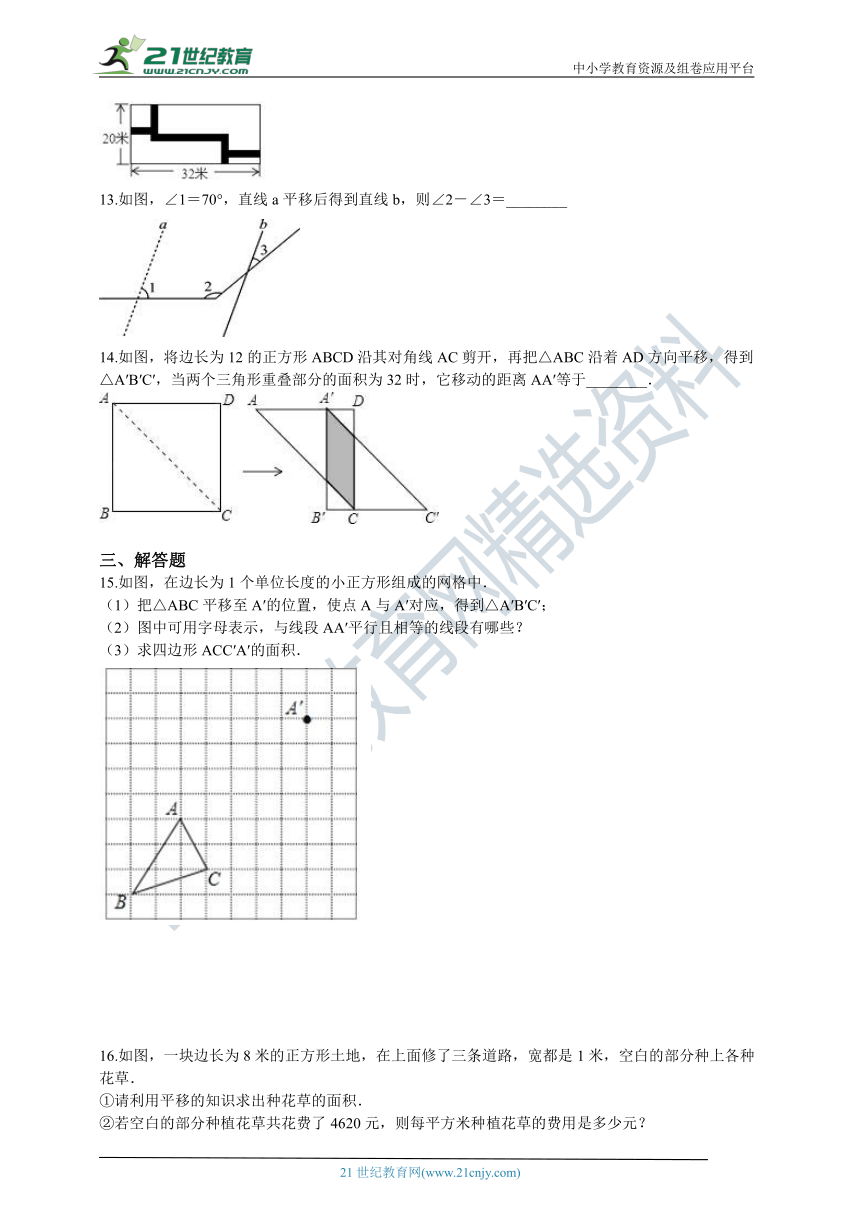
12.如图所示，某住宅小区内有一长方形地块，想在长方形地块内修筑同样宽的两条”之”字路，余下部分绿化，道路的宽为2m，则绿化的面积为________m2 ．
13.如图，∠1＝70°，直线a平移后得到直线b，则∠2－∠3＝________
14.如图，将边长为12的正方形ABCD沿其对角线AC剪开，再把△ABC沿着AD方向平移，得到△A′B′C′，当两个三角形重叠部分的面积为32时，它移动的距离AA′等于________．
三、解答题
15.如图，在边长为1个单位长度的小正方形组成的网格中．（1）把△ABC平移至A′的位置，使点A与A′对应，得到△A′B′C′；（2）图中可用字母表示，与线段AA′平行且相等的线段有哪些？（3）求四边形ACC′A′的面积．
16.如图，一块边长为8米的正方形土地，在上面修了三条道路，宽都是1米，空白的部分种上各种花草．①请利用平移的知识求出种花草的面积．②若空白的部分种植花草共花费了4620元，则每平方米种植花草的费用是多少元？
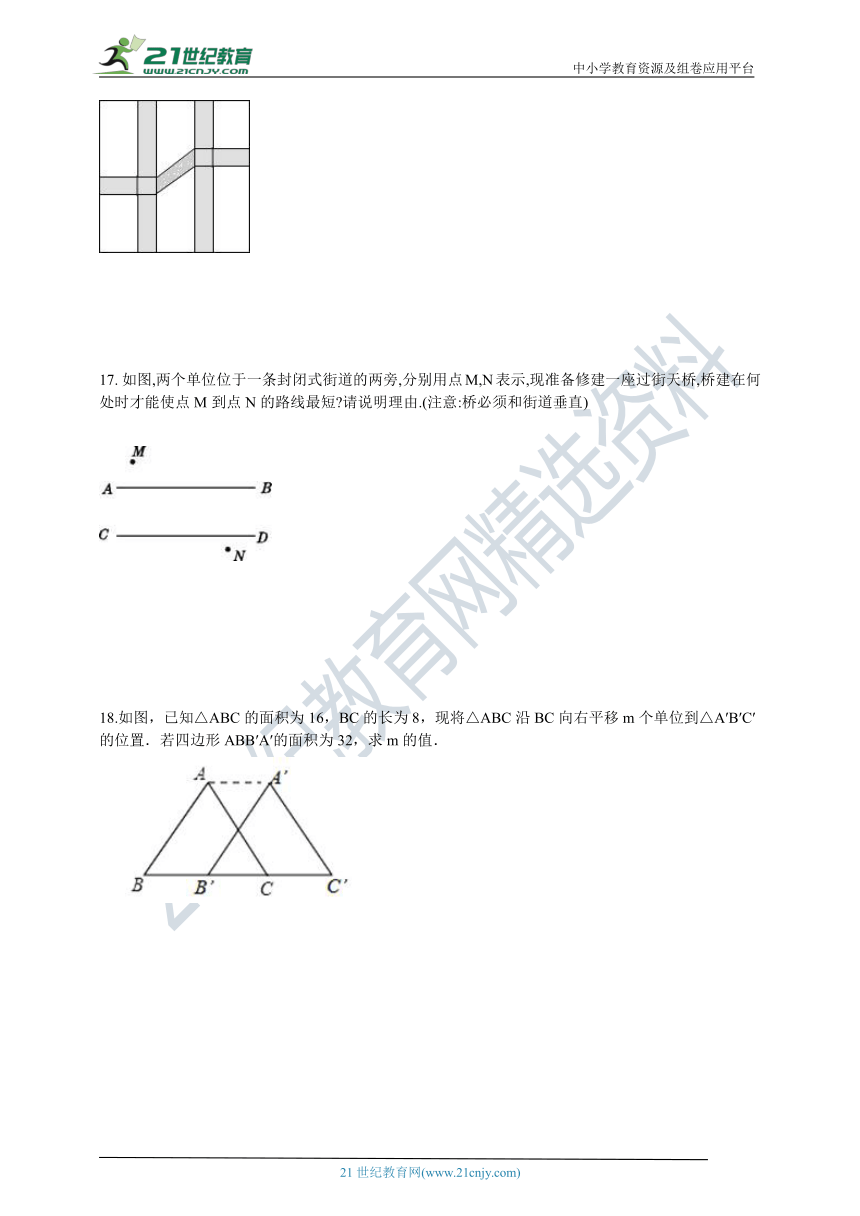
如图,两个单位位于一条封闭式街道的两旁,分别用点M,N表示,现准备修建一座过街天桥,桥建在何处时才能使点M到点N的路线最短?请说明理由.(注意:桥必须和街道垂直)

18.如图，已知△ABC的面积为16，BC的长为8，现将△ABC沿BC向右平移m个单位到△A′B′C′的位置．若四边形ABB′A′的面积为32，求m的值．
参考答案与试题解析
一、单选题
1.B
解：∵△ABC向右平移5个单位长度得到△DEF∴BE=5∵EC= 4 ，∴BC=BE+EC=5+4=9
故答案为：B
2.D
解: 通过作辅助线，由平行线性质可选D项故答案为：D
3.C
解：由分析可知：在图形的平移中，下列说法中错误的是：图形上可能存在不动点；
故答案为：C
4.A
解：观察图形可知，图案A可以看作由基本图案“圆”经过平移得到的.
故答案为：A．
5.D
解：由平移的特征，平移前后的两个图形的形状与大小都没有发生变化，故A，B，C均成立，所以只有D符合题意．故答案为：D
6.A
解：平移步骤是：先把△ABC向左平移5个单位，再向下平移2个单位，
故答案为：A．
7.C
解：把△OB C向右上方平行移动，可得△OAF，
故答案为：C．
8.B
解： (2)(4)(5)是平移；(1)(3)(6)不是平移故答案为：B
二、填空题
9.30°
解：由平移的性质知,∠CAB=∠EBD=50°,又∠ABC=100°,所以∠CBE=180°-∠ABC-∠EBD=180°-100°-50°=30°.故答案为:30°
10.8
解：∵将△ABC沿CB向右平移得到△DEF，平移距离为2，∴AD∥BE，AD=BE=2，∴四边形ABED是平行四边形，∴四边形ABED的面积=BE×AC=2×4=8．故答案为：8．
11.13
解：∵将线段DC沿着CB的方向平移7cm得到线段EF， ∴EF=DC=4cm，FC=7cm，∵AB=AC，BC=12cm，∴∠B=∠C，BF=5cm，∴∠B=∠BFE，∴BE=EF=4cm，∴△EBF的周长为：4+4+5=13（cm）．故答案为：13．
12.540
解：如图，把两条“之”字路平移到长方形地块ABCD的最上边和最左边，则余下部分EFGH是矩形. ∵CF=32?2=30(米),CG=20?2=18(米)，∴矩形EFCG的面积=30×18=540(平方米).故答案为：540.
13.110°
解：过∠2的折点作平行线C,从而得到∠2－∠3=180°-70°=110°故答案为：
14.4或8 解：由题意可知阴影部分是平行四边形，△AA′H与△HCB′都是等腰直角三角形，若设AA′=x，则阴影部分的底长为x，高A′D=12-x，∴x（12-x）=32，解得x=4或8，即AA′=4或8cm．故答案为：4或8
三、解答题
15.解：（1）△A′B′C′如图所示；（2）由平移的性质，与线段AA′平行且相等的线段有BB′、CC′；故答案为：BB′、CC′；（3）四边形ACC′A′的面积=6×6﹣×1×2﹣×5×4﹣×1×2﹣×5×4=36﹣1﹣10﹣1﹣10=36﹣22=14．
16.解：①（8－2）×（8－1）＝6×7＝42?（米2）答：种花草的面积为42米2 ． ②4620÷42＝110（元）答：每平方米种植花草的费用是110元．
17.解: ①作NE⊥AB于点E,交CD于点F; ②在NE上截取NN'=EF;③连接MN',交AB于点P;④过点P作PQ⊥AB,交CD于点Q,如图,则PQ为过街天桥应建的位置.理由:如图,连接QN.∵PQ⊥AB,NE⊥AB,∴PQ∥NE.又∵NN'=EF,EF=PQ,∴PQ=NN'(相当于将PQ平移到NN').∴QN=PN'.∴MP+PN'最短(两点之间线段最短),PQ为定值.∴桥建在PQ处时才能使点M到点N的路线最短.
18.解：如图1，过点A向BC作垂线，垂足为H，
∵△ABC的面积=16，BC=8，∴×BC×AH=16，∴，解得AH=4，又∵四边形ABB′A′的面积为32，∴BB′×4=32，∴BB′=32÷4=8，∴m=BB′=8，即m的值是8．