1.4平行线的性质（1）课件

1.4平行线的性质(1)
浙教版 七年级下
新知导入
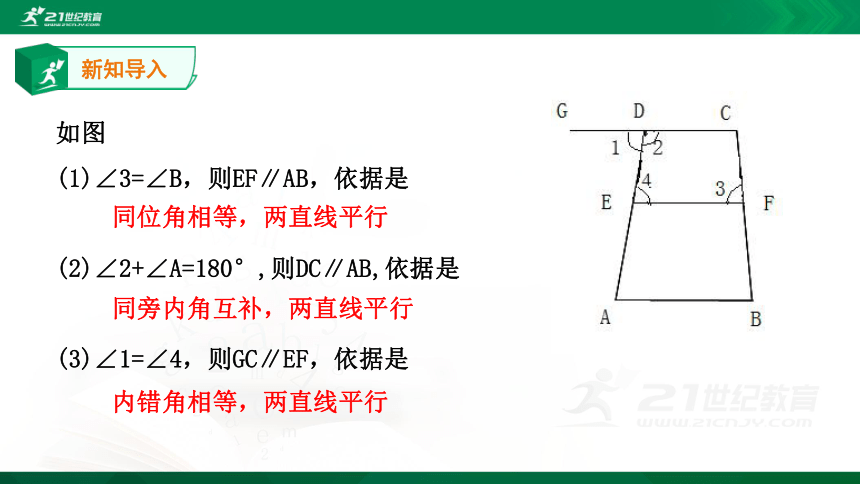
如图
(1)∠3=∠B，则EF∥AB，依据是

(2)∠2+∠A=180°,则DC∥AB,依据是

(3)∠1=∠4，则GC∥EF，依据是


同位角相等，两直线平行
同旁内角互补，两直线平行
内错角相等，两直线平行
新知导入
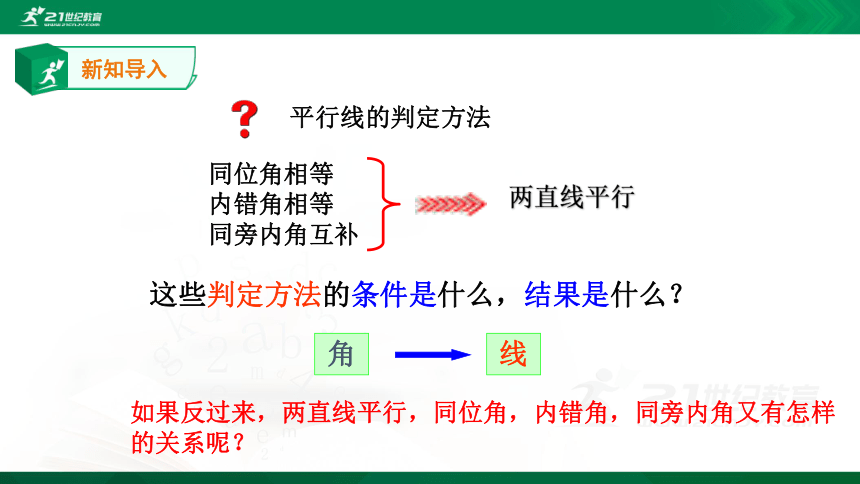
平行线的判定方法
同位角相等
内错角相等
同旁内角互补
两直线平行
如果反过来，两直线平行，同位角，内错角，同旁内角又有怎样的关系呢？
这些判定方法的条件是什么，结果是什么？
角
线
新知讲解
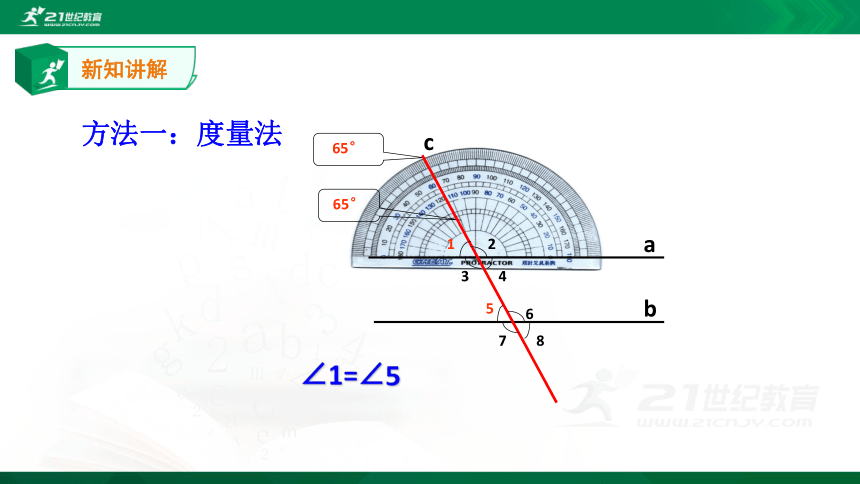
任意画两条互相平行的直线，再任意画一条直线与这两条平行线相交.测量同位角的度数，你发现了什么?与其他同学的发现相同吗？
新知讲解
65°
65°
c
a
b
1
5
2
3
4
6
7
8
∠1=∠5
方法一：度量法
新知讲解
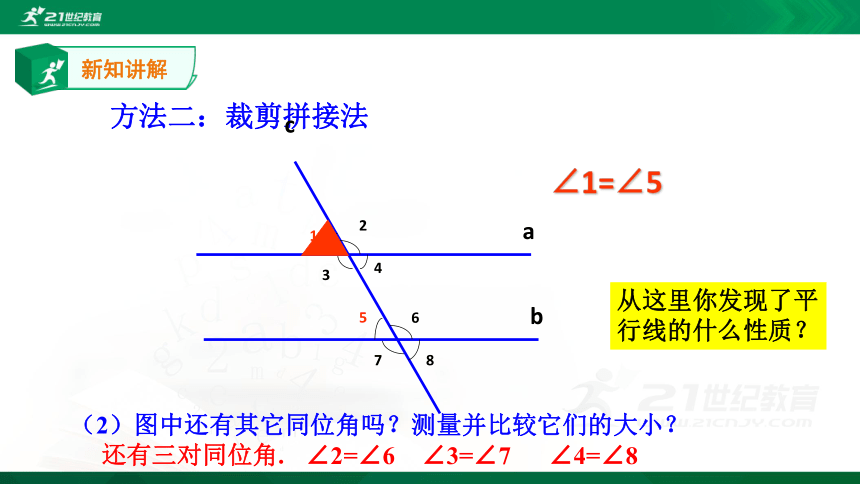
方法二：裁剪拼接法
6
8
a
c
2
3
4
7
1
∠1=∠5
（2）图中还有其它同位角吗？测量并比较它们的大小？
还有三对同位角.
∠2=∠6
∠3=∠7 ∠4=∠8
从这里你发现了平行线的什么性质？
新知讲解

图中还有其它同位角吗？它们的大小有什么关系？
简记为：两直线平行，同位角相等
如果两条平行直线被第三条直线所截，同位角相等
由此得到平行线的性质：
数学语言表示：
∵ a//b (已知)
∴ ∠1=∠2 (两直线平行,同位角相等)
新课讲解
判定定理
同位角相等
平行线判定定理和性质定理有什么区别？
发现：二者条件与结论正好相反
性质定理
条件
结论
条件
结论
两直线平行
同位角相等
两直线平行
新知讲解
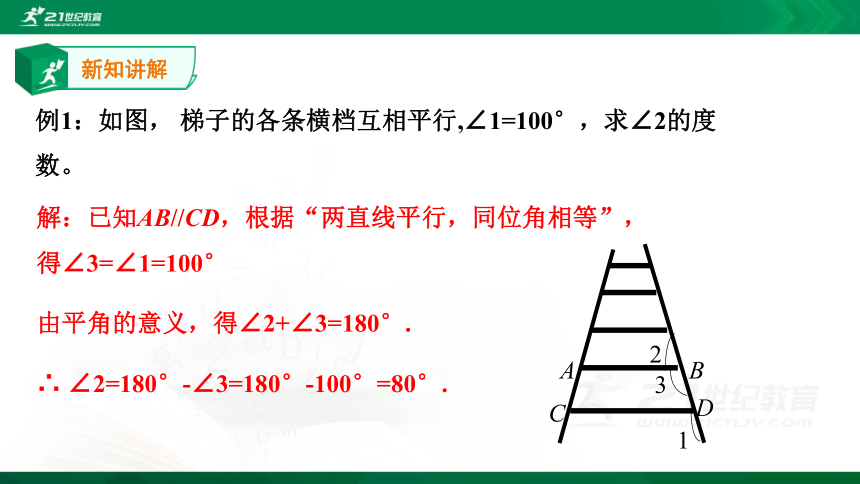
例1：如图， 梯子的各条横档互相平行,∠1=100°，求∠2的度数。
A
B
C
D
2
3
1
解：已知AB//CD，根据“两直线平行，同位角相等”，得∠3=∠1=100°
由平角的意义，得∠2+∠3=180°.
∴ ∠2=180°-∠3=180°-100°=80°.
新知讲解
例2： 如图：已知∠1=∠2.若直线b⊥m，则直线a⊥m，请说明理由.
新知讲解
解：如图1-17，已知∠1=∠2，
根据“同位角相等，两直线平行”，得a//b，
由a//b，再根据“两直线平行，同位角相等”，
得∠3=∠4，又已知b⊥m ，
根据垂直的意义，得∠4=90°
∴ ∠3=90° ∴ a⊥m（垂直的意义）
课堂练习
1、如图，直线a∥b，直线c与a，b相交，∠1＝70°，
则∠2的大小是(　　)
A．20°　　　　　　　B．50°　　　　　　　
C．70°　　　　　　　D．110°
2 如图，直线l1∥l2，直线l3与l1，l2分别交于A，B两点，若∠1＝70°，则∠2＝(　　)
A．70° B．80° C．110° D．120°


C
C
课堂练习
3. 已知∠3 =∠4，∠1=47°, 求∠2的度数？
解：∵ ∠3 =∠4(已知 )
∴a∥b(同位角相等，两直线平行)
∴∠1=∠2(两直线平行，同位角相等)
∵∠1= 47°(已知 )
∴∠2= 47°（等量代换）
拓展提高
如图，△ABC中，D是AB上一点， E是AC上一点， ∠ADE＝60°，∠B＝60°，∠AED＝40°。
⑴ DE和BC平行吗？为什么？
⑵ ∠C是多少度？为什么？
解：⑴ DE∥BC，理由如下：
∵∠ADE＝60°，∠B＝60° (已知)
∴ ∠ADE＝∠B (等量代换)
∴ DE∥BC (同位角相等，两直线平行)
拓展提高
如图，△ABC中，D是AB上一点， E是AC上一点， ∠ADE＝60°，∠B＝60°，∠AED＝40°。
⑴ DE和BC平行吗？为什么？
⑵ ∠C是多少度？为什么？
⑵ 由⑴知 DE∥BC
∵∠AED＝60° (已知)
∴ ∠C＝∠AED (两直线平行，同位角相等)
∴ ∠C＝60° (等量代换)
课堂总结
同位角相等，两直线平行。
两直线平行，同位角相等。
判定方法1
性质1
板书设计
同位角相等，两直线平行。
两直线平行，同位角相等。
判定方法1
性质1
简记为：两直线平行，同位角相等
如果两条平行直线被第三条直线所截，同位角相等
数学语言表示：
∵ a//b (已知)
∴ ∠1=∠2 (两直线平行,同位角相等)
作业布置
教材第16页习题第1、2题
谢谢
21世纪教育网（www.21cnjy.com) 中小学教育资源网站
有大把高质量资料？一线教师？一线教研员？
欢迎加入21世纪教育网教师合作团队！！月薪过万不是梦！！
详情请看：
https://www.21cnjy.com/help/help_extract.php