1.4平行线的性质（2）课件

1.4平行线的性质（2）
浙教版 七年级下
新知导入
性质1：两直线平行，同位角相等 。
∵AB ∥CD( )
已知
∴ ∠1= ∠2
( )
两直线平行 同位角相等
平行线还有哪些性质？
新知讲解
如图，直线AB//CD，并被直线EF所截.∠2与∠3相等吗？∠3与∠4的和是多少度？
建议从以下几方面思考：
(1)回顾我们已经知道的平行线的性质，由此能得
出图中哪一对角相等？
(2)∠3与∠1有什么关系？∠4与∠2呢？
你发现平行线还有哪些性质？
∠2=∠3,∠3+∠4=180°.
⑴∠1=∠2.
⑵∠3=∠1，∠4=∠2互补.
平行线的性质还有“两直线平行，内错角相等”“两直线平行，同旁内角互补”.
新知讲解
归纳：平行线的性质2
两条平行线被第三条直线所截，内错角相等。
简单地说，两直线平行，内错角相等。
∵AB∥CD( )
∴∠2=∠3
( )
已知
两直线平行，内错角相等
∵∠1=∠3，∠1=∠2
∴∠2=∠3(等量代换)
新知讲解
归纳：平行线的性质3
两条平行线被第三条直线所截，同旁内角互补。
简单地说，两直线平行，同旁内角互补。
∵AB∥CD( )
已知
∴∠3+∠4=180?
（ ）
两直线平行，同旁内角互补
∵∠2=∠3， ∠2+∠4=180°
∴∠3+∠4=180° (等量代换)
新知讲解
两直线平行
判定
性质
已知
结论
结论
已知
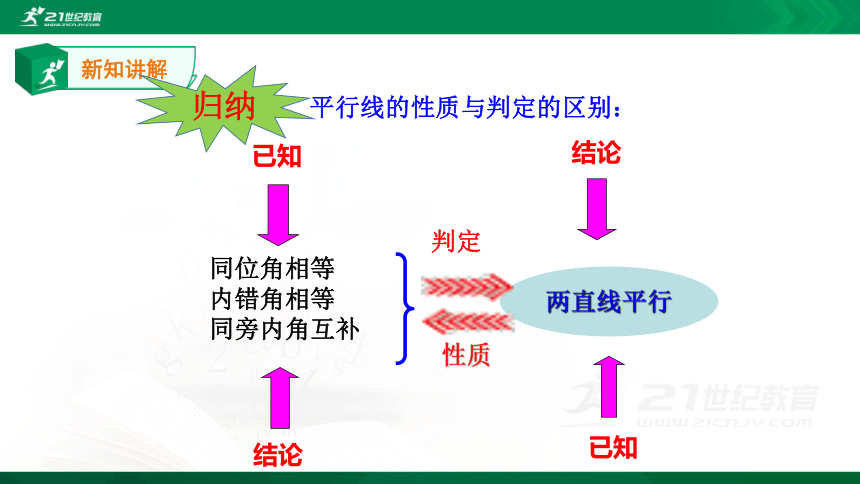
平行线的性质与判定的区别：
同位角相等
内错角相等
同旁内角互补
归纳
新知讲解
例3.如图,已知AB∥CD，AD∥BC。判断∠1与∠2是否相等，并说明理由。
解：∵AB∥CD（已知）
∴ ∠1+ ∠BAD=1800
（两直线平行，同旁内角互补）
∴∠1=∠2
（同角的补角相等）
∵AD∥BC（已知）
∴ ∠2+ ∠BAD=1800
（同理）
新知讲解
例4：如图,已知∠ABC+∠C=180°,BD平分∠ABC。∠CBD与∠D相等吗？请说明理由。
A
B
D
C
解：∠CBD=∠D。理由如下：
∵∠ABC+∠C=1800（已知）
∴AB∥CD
（同旁内角互补，两直线平行）
∴∠D=∠ABD
（两直线平行，内错角相等）
又∵BD平分∠ABC
∴∠CBD=∠ABD=∠D
新知讲解
平行线的性质2：
两条平行线被第三条直线所截，内错角相等。
简单地说，两直线平行，内错角相等。
平行线的性质3：
两条平行线被第三条直线所截，同旁内角互补。
简单地说，两直线平行，同旁内角互补。
课堂练习
1．如图，AB，CD被EF所截，AB//CD.　
　 按要求填空：
若∠1＝120°，则∠2＝_＿__°（　　　　　　　　　　 ）；
∠3＝＿＿＿－ ∠1＝＿＿°（　　　　　　　　　　　 ）
1
2
3
120
180°
60
两直线平行，内错角相等．
两直线平行，同旁内角互补．
课堂练习
　　2．如图，在甲、乙两地之间要修一条笔直的公路，从甲地测得公路的走向是南偏西56°，甲、乙两地同时开工，若干天后公路准确接通，则乙地所修公路的走向是__________，因为______________________________．
两直线平行，内错角相等
北偏东56°
课堂练习
3．如图，△ABC的边AB//CE，则：　
　 ∠A＝ ∠＿＿（　　　　　　　　　　 ）；
　 ∠B＝ ∠＿＿（　　　　　　　　　　 ）．
　　运用刚才的推理，可以说明一个结论，
你想到了吗？
思考:
三角形的三个内角和等于180°
2
两直线平行，内错角相等．
1
两直线平行，同位角相等．
课堂练习
4. 如图，AB∥CD，∠1=∠2，∠3=∠4．
求证：PM∥NQ．
证明：
∵∠1=∠2 ，∠3=∠4，
又∵∠2=∠3．
∴∠1=∠2 =∠3=∠4．
∵∠1+∠2 +∠5=180?，
∠3+∠4 +∠6=180?，
∴∠5=∠6．
∴ PM∥NQ （内错角相等，两直线平行）．
课堂总结
判定方法1: 同位角相等，两直线平行.
判定方法2: 内错角相等，两直线平行.
判定方法3: 同旁内角互补，两直线平行.
　平行线的判定
板书设计
平行线的性质2
两条平行线被第三条直线所截，内错角相等。
简单地说，两直线平行，内错角相等。
∵AB∥CD( )
∴∠2=∠3
( )
已知
两直线平行，内错角相等
板书设计
平行线的性质3
两条平行线被第三条直线所截，同旁内角互补。
简单地说，两直线平行，同旁内角互补。
∵AB∥CD( )
已知
∴∠3+∠4=180?
（ ）
两直线平行，同旁内角互补
作业布置
教材第19页习题第1、2题
谢谢
21世纪教育网（www.21cnjy.com) 中小学教育资源网站
有大把高质量资料？一线教师？一线教研员？
欢迎加入21世纪教育网教师合作团队！！月薪过万不是梦！！
详情请看：
https://www.21cnjy.com/help/help_extract.php