第二章 二元一次方程组解答题精选

绝密★启用前
第二章二元一次方程组解答题精选
题号
一
总分
得分
注意事项：
1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上
请点击修改第I卷的文字说明
评卷人
得 分


解答题（共40小题）
1．解方程组
（1）
（2）．
2．解方程组
（1）
（2）．
3．已知关于x，y的方程组和有相同解，求（﹣a）b值．
4．如果关于x、y的二元一次方程组的解是，求关于x、y的方程组的解：
（1）
（2）
5．已知：都是关于x、y方程y+mx＝1的解，
（1）若a＝b＝3，求m的值并直接写出c和d的关系式；
（2）a+c＝12，b+d＝4m+4，比较b和d的大小．
6．我们用[a]表示不大于a的最大整数，例如：[2.5]＝2，[3]＝3，[﹣2.5]＝﹣3，用＜a＞表示大于a的最小整数．例如：＜2.5＞＝3，＜4＞＝5，＜﹣1.5＞＝﹣1．解决下列问题：
（1）[﹣2.6]＝　 　，＜6.2＞＝　 　．
（2）已知x，y满足方程组，则[x]＝　 　，＜y＞＝　 　，x的取值范围是　 　，y的取值范围是　 　．
7．已知关于x、y的方程组的解满足x+y＝2，求k的值．
8．已知代数式kx+b，当x＝﹣3，x＝2时，代数式的值分别是1和11，求代数式的值为﹣3时，x的值．
9．在解方程组时，由于粗心，甲看错了方程组中的a，而得到解为，乙看错了方程组中的b，而得到解为．
（1）求正确的a，b的值；
（2）求原方程组的解．
10．解方程组：
11．已知和是关于x，y的二元一次方程y＝kx+b的解，求k，b的值．
12．已知方程组和的解相同，求代数式（4a﹣3b）2018的值．
13．解方程组
（1）
（2）
14．对于任意实数a，b，定义关于“?”的一种运算如下：a?b＝2a+b．例如3?4＝2×3+4＝10．
（1）求2?（﹣5）的值；
（2）若x?（﹣y）＝2，且2y?x＝﹣1，求x+y的值．
15．解方程组：
（1）2x﹣y＝x+y＝3；
（2）．
16．解关于x、y方程组可以用（1）×2+（2）消去未知数x；也可以用（1）+（2）×5消去未知数y；求m、n的值．
17．已知关于x，y的方程组的解满足x+2y＝2．
（1）求m的值；
（2）若a≥m，化简：|a+1|﹣|2﹣a|．
18．（1）阅读以下内容：
已知实数x，y满足x+y＝2，且求k的值．
三位同学分别提出了以下三种不同的解题思路：
甲同学：先解关于x，y的方程组，再求k的值．
乙同学：先将方程组中的两个方程相加，再求k的值．
丙同学：先解方程组，再求k的值．
（2）你最欣赏（1）中的哪种思路？先根据你所选的思路解答此题，再对你选择的思路进行简要评价．
（评价参考建议：基于观察到题目的什么特征设计的相应思路，如何操作才能实现这些思路、运算的简洁性，以及你依此可以总结什么解题策略等等）
19．根据要求，解答下列问题．
（1）解下列方程组（直接写出方程组的解即可）：
A. B. C.
方程组A的解为　 　，方程组B的解为　 　，方程组C的解为　 　；
（2）以上每个方程组的解中，x值与y值的大小关系为　 　；
（3）请你构造一个具有以上外形特征的方程组，并直接写出它的解．
20．根据要求，解答下列问题．
（1）解方程组：．
（2）解下列方程组，只写出最后结果即可：①；②．
（3）以上每个方程组的解中，x值与y值有怎样的大小关系？
（4）观察以上每个方程组的外形特征，请你构造一个具有此特征的方程组，并用（3）中的结论快速求出其解．
21．《九章算术》是中国古代的数学专著，下面这道题是《九章算术》中第七章的一道题：“今有共买物，人出八，盈三；人出七，不足四，问人数，物价各几何？”译文：“几个人一起去购买物品，如果每人出8钱，则多了3钱；如果每人出7钱，则少了4钱，求有多少人，物品的价格是多少”．
22．某服装店用4400元购进A，B两种新式服装，按标价售出后可获得毛利润2800元（毛利润＝售价﹣进价），这两种服装的进价，标价如表所示．
类型价格
　A型
　B型
　进价（元/件）
　60
　100
　标价（元/件）
　100
　160
（1）请利用二元一次方程组求这两种服装各购进的件数；
（2）如果A种服装按标价的9折出售，B种服装按标价的8折出售，那么这批服装全部售完后，服装店比按标价出售少收入多少元？
23．
如图为地铁调价后的计价表．调价后小明、小伟从家到学校乘地铁分别需要4元和3元．由于刷卡坐地铁有优惠，因此，他们平均每次实付3.6元和2.9元．已知小明从家到学校乘地铁的里程比小伟从家到学校的里程多5km，且小明每千米享受的优惠金额是小伟的2倍，求小明和小伟从家到学校乘地铁的里程分别是多少千米？
24．小阳骑车和步行的速度分别为240米/分钟和80米/分钟，小红每次从家步行到学校所需时间相同．请根据两人的对话解决如下问题：小阳：“如果我骑车，你步行，那么我从家到学校比你少用4分钟”小红：“如果我们俩都步行，那么从家到学校我比你少用2分钟．”若设小阳从家到学校的路程为x米，小红从家到学校所需的时间为y分钟．
（1）小阳从家到学校骑车的时间是　 　分钟，步行的时间是　 　分钟（用含x的式子表示）．
（2）求x，y的值．
25．[阅读?领会]
怎样判断两条直线是否平行？
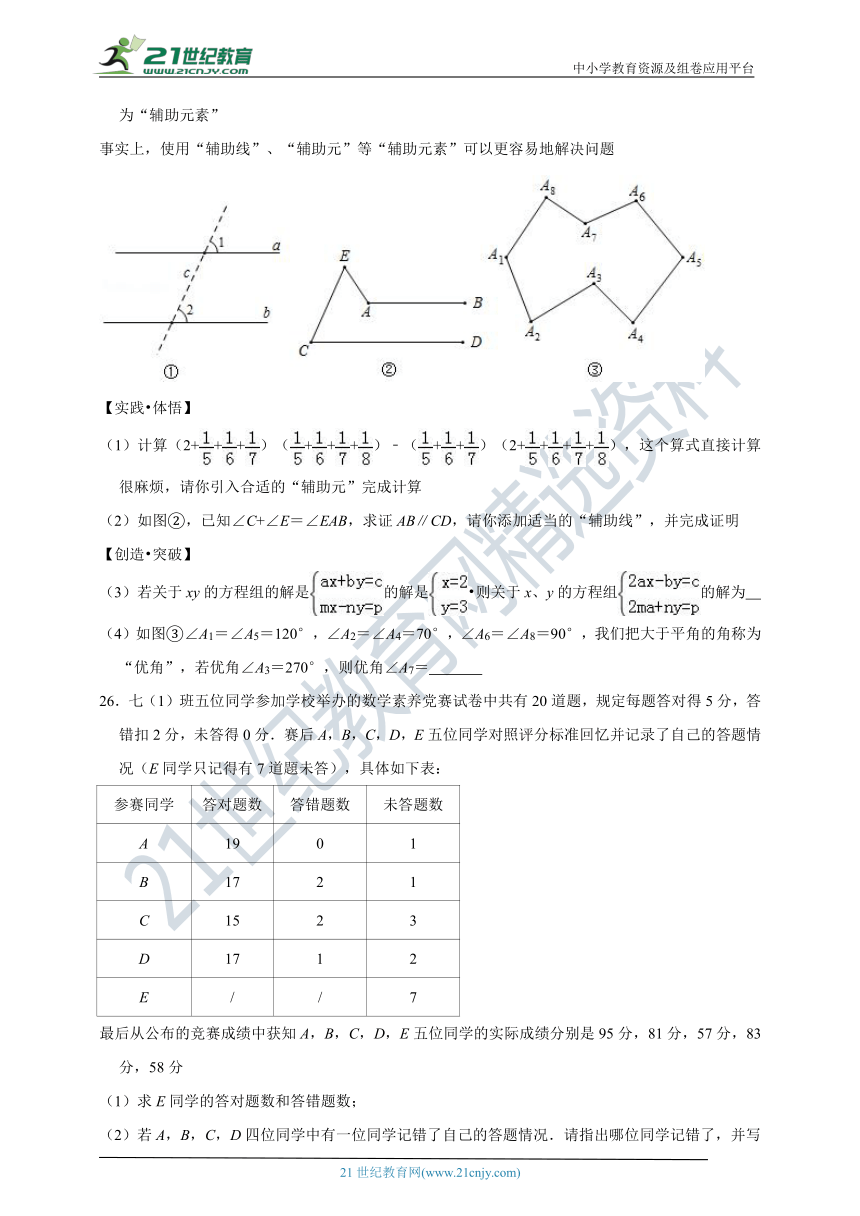
如图①，很难看出直线a、b是否平行，可添加“第三条线”（截线c），把判断两条直线的位置关系转化为判断两个角的数量关系．我们称直线c为“辅助线”．
在部分代数问题中，很难用算术直接计算出结果，于是，引入字母解决复杂问题，我们称引入的字母为“辅助元素”
事实上，使用“辅助线”、“辅助元”等“辅助元素”可以更容易地解决问题
【实践?体悟】
（1）计算（2+++）（+++）﹣（++）（2++++），这个算式直接计算很麻烦，请你引入合适的“辅助元”完成计算
（2）如图②，已知∠C+∠E＝∠EAB，求证AB∥CD，请你添加适当的“辅助线”，并完成证明
【创造?突破】
（3）若关于xy的方程组的解是的解是?则关于x、y的方程组的解为　 　
（4）如图③∠A1＝∠A5＝120°，∠A2＝∠A4＝70°，∠A6＝∠A8＝90°，我们把大于平角的角称为“优角”，若优角∠A3＝270°，则优角∠A7＝　 　
26．七（1）班五位同学参加学校举办的数学素养党赛试卷中共有20道题，规定每题答对得5分，答错扣2分，未答得0分．赛后A，B，C，D，E五位同学对照评分标准回忆并记录了自己的答题情况（E同学只记得有7道題未答），具体如下表：
参赛同学
答对题数
答错题数
未答题数
A
19
0
1
B
17
2
1
C
15
2
3
D
17
1
2
E
/
/
7
最后从公布的竞赛成绩中获知A，B，C，D，E五位同学的实际成绩分别是95分，81分，57分，83分，58分
（1）求E同学的答对题数和答错题数；
（2）若A，B，C，D四位同学中有一位同学记错了自己的答题情况．请指出哪位同学记错了，并写出他的实际答题情况．
27．某公司以每吨600元的价格收购了100吨某种药材，若直接在市场上销售，每吨的售价是1000元，该公司决定加工后再出售，相关信息如下表所示：
工艺
每天可加工药材的吨数
成品率
成品售价
粗加工
14
80%
6000
精加工
6
60%
11000
（注：①成品率80%指加工100吨原料能得到80吨可销售药材；②加工后的废品不产生效益）
受市场影响，该公司必须在10天内将这批药材加工完毕．
（1）若全部粗加工，可获利　 　元；
（2）若尽可能多的精加工，剩余的直接在市场上销售，可获利　 　元；
（3）若部分粗加工，部分精加工，恰好10天完成，求可获利多少元？
28．在我市“精准扶贫”工作中，甲、乙两个工程队先后接力为扶贫村庄修建一条210米长的公路，甲队每天修建15米，乙队每天修建25米，一共用10天完成．
根据题意，小红和小芳同学分别列出了下面尚不完整的方程组：
小红：小芳：
（1）请你分别写出小红和小芳所列方程组中未知数x，y表示的意义：
小红：x表示　 　，y表示　 　；
小芳：x表示　 　，y表示　 　；
（2）在题中“（　　）”内把小红和小芳所列方程组补充完整；
（3）甲工程队一共修建了　 　天，乙工程队一共修建了　 　米．
29．春天来了，石头城边，秦淮河畔，鸟语花香，柳条飘逸．为给市民提供更好的休闲锻炼环境，决定对一段总长为1800米的外秦淮河沿河步行道出新改造，该任务由甲、乙两工程队先后接力完成．甲工程队每天改造12米，乙工程队每天改造8米，共用了200天．
（1）根据题意，小莉、小刚两名同学分别列出了尚不完整的方程组如下：
小莉：小刚：
根据两名同学所列的方程组，请你分别指出未知数x、y表示的意义，然后补全小莉、小刚两名同学所列的方程组：
小莉：x表示　 　，y表示　 　；
小刚：x表示　 　，y表示　 　；
（2）求甲、乙两工程队分别出新改造步行道多少米．
30．小明是一个乐思好问的学生，在解答七年级下册教材中一道拓广探索题时遇到了困难．这道题是这样的：
一个长方形的长减少5cm，宽增加2cm，就成为一个正方形，并且这两个图形的面积相等．这个长方形的长、宽各是多少？
（1）如图，设长方形的长、宽各是xcm，ycm，小明绞尽脑汁列出了三个不同的方程组：
①，②，③
以上三个方程组中，能正确反映题意的有　 　．（请直接填写序号）
（2）小明列出的方程，根据目前知识不易求解，便请教老师，老师提示这个问题可以列二元一次方程组来解答，并适时点拨，小明终于明白了．请你写出小明列出的二元一次方程组，并写出解题过程．
31．某公司要把一批货物运往A地，准备租用汽车运输公司的甲乙两种货车．过去曾两次租用这两种货车的情况如表：
第一次
第二次
租用甲种货车（辆）
2
5
租用乙种货车（辆）
3
6
合计运货吨数（吨）
15.5
35
现租用该公司甲种货车3辆，乙种货车5辆，正好运完这批货，如果每吨货物的运费为30元，这批货物应该付运费多少元？
32．某校组织七年级全体师生乘旅游客车前往广州开展研学旅行活动．旅游客车有大小两种，2辆大客车与3辆小客车全部坐满可乘载195人，4辆大客车与2辆小客车全部坐满可乘载250人，全体师生刚好坐满12辆大客车与10辆小客车，问该校七年级师生共有多少人？
33．《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．它的代数成就主要包括开放术、正负术和方程术．其中，方程术是《九章算术》最高的数学成就．《九章算术》中记载：“今有牛五、羊二，直金十两；牛二、羊五，直金八两．问牛、羊各直金几何？”
译文：“假设有5头牛、2只羊，值金10两；2头牛、5只羊，值金8两．问每头牛、每只羊各值金多少两？”
34．某运动员在一场篮球比赛中的技术统计如表所示：
技术
上场时间
（分钟）
出手投篮
（次）
投中
（次）
罚球得分
篮板
（个）
助攻
（次）
个人总得分
数据
46
66
22
10
11
8
60
注：表中出手投篮次数和投中次数均不包括罚球．投篮投不中不得分，罚球投中一球得1分，除罚球外投中一球得2分或3分．
根据以上信息，求本场比赛中该运动员投中2分球和3分球各几个．
35．分别用8个大小一样的长方形拼图．如图①，小明拼成了一个大的长方形；如图②，小红拼成了一个大的正方形，但中间恰好空出一个边长为1mm的小正方形．你能求出小长方形的长和宽吗？
36．我国古代数学著作《九章算术》中有这样一题，原文是：“今有大器五小器一容三斛，大器一小器五容二斛，问大小器各容几何．”意思是：有大小两种盛酒的桶，已知5个大桶加上1个小桶可以盛酒3斛（斛，是古代的一种容量单位），1个大桶加上5个小桶可以盛酒2斛．1个大桶、1个小桶分别可以盛酒多少斛？请解答．
37．在国家积极推进“互联网+”行动以来，网上购物已成为生活中的新常态．某甲在网购平台上购买商品A、B共三次，只有一次购买时，商品A、B同时打折，其余两次均按标价购买，三次购买商品A、B的数量和费用如下表：
购买商品A的数量（个）
购买商品B的数量（个）
购买总费用（元）
第一次购物
6
4
240
第二次购物
8
6
204
第三次购物
5
6
280
（1）某甲第　 　次购物时，商品A、B同时打折，并简略叙述理由．
理由为：　 　．
（2）请求出商品A的标价．
38．随着“互联网+”时代的到来，一种新型打车方式受到大众欢迎，该打车方式的总费用由里程费和耗时费组成，其中里程费按x元/公里计算，耗时费按y元/分钟计算（总费用不足9元按9元计价）．小明、小刚两人用该打车方式出行，按上述计价规则，其打车总费用、行驶里程数与打车时间如表：
时间（分钟）
里程数（公里）
车费（元）
小明
8
8
12
小刚
12
10
16
（1）求x，y的值；
（2）如果小华也用该打车方式，打车行驶了11公里，用了14分钟，那么小华的打车总费用为多少？
39．某市为了鼓励居民节约用水，决定实行两级收费制度，若每月用水量不超过14吨（含14吨），则每吨按政府补贴优惠价m元收费；若每月用水量超过14吨，则超过部分每吨按市场价n元收费．小明家3月份用水20吨，交水费49元；4月份用水18吨，交水费42元．
（1）求每吨水的政府补贴优惠价m和市场价n分别是多少元？
（2）小明家5月份交水费70元，则5月份他家用了多少吨水？
40．奖励在演讲比赛中获奖的同学，班主任派学习委员小明为获奖同学买奖品，要求每人一件，小明到文具店看了商品后，决定奖品在钢笔和笔记本中选择，如果买4个笔记本和2支钢笔，则需86元；如果买3个笔记本和1支钢笔，则需57元．
（1）求购买每个笔记本和钢笔分别为多少元？
（2）售货员提示，买钢笔有优惠，具体方法是：如果买钢笔超过10支，那么超出部分可以享受8折优惠，若买15支钢笔，20个笔记本，一共花多少钱？

参考答案与试题解析
一．解答题（共40小题）
1．解方程组
（1）
（2）．
【分析】（1）方程组利用加减消元法求出解即可；
（2）方程组整理后，利用加减消元法求出解即可．
【解答】解：（1），
②﹣①得：8y＝﹣8，
解得：y＝﹣1，
把y＝﹣1代入①得：x＝1，
则方程组的解为；
（2）方程组整理得：，
①﹣②得：4y＝26，
解得：y＝，
把y＝代入①得：x＝，
则方程组的解为．
【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
2．解方程组
（1）
（2）．
【分析】（1）方程组利用代入消元法求出解即可；
（2）方程组整理后，利用加减消元法求出解即可．
【解答】解：（1），
把①代入②得：3x+2x﹣4＝1，
解得：x＝1，
把x＝1代入①得：y＝﹣2，
则方程组的解为；
（2）方程组整理得：，
①×2﹣②得：3y＝9，
解得：y＝3，
把y＝3代入②得：x＝5，
则方程组的解为．
【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
3．已知关于x，y的方程组和有相同解，求（﹣a）b值．
【分析】因为两个方程组有相同的解，故只要将两个方程组中不含有a，b的两个方程联立，组成新的方程组，求出x和y的值，再代入含有a，b的两个方程中，解关于a，b的方程组即可得出a，b的值．
【解答】解：因为两组方程组有相同的解，所以原方程组可化为
，
解方程组（1）得，
代入（2）得．
所以（﹣a）b＝（﹣2）3＝﹣8．
【点评】此题比较复杂，考查了学生对方程组有公共解定义的理解能力及应用能力，是一道好题．
4．如果关于x、y的二元一次方程组的解是，求关于x、y的方程组的解：
（1）
（2）
【分析】（1）仿照已知方程组的解，列出关于x、y的方程组，求出方程组的解即可得到x、y的值即可；
（2）仿照已知方程组的解，列出关于x、y的方程组，求出方程组的解即可得到x、y的值即可．
【解答】解：∵关于x、y的二元一次方程组的解是，
∴（1），
解得；
（2），
解得．
【点评】此题考查了二元一次方程组的解，利用了类比的方法，弄清题中方程组解的特征是解本题的关键．
5．已知：都是关于x、y方程y+mx＝1的解，
（1）若a＝b＝3，求m的值并直接写出c和d的关系式；
（2）a+c＝12，b+d＝4m+4，比较b和d的大小．
【分析】（1）把a＝b＝3代入方程y+mx＝1，可求m的值，进一步得到c和d的关系式；
（2）列出关于a、b、c、d的方程组，并求出m的值，计算b﹣d的差的正负得结果..
【解答】④解：（1）∵a＝b＝3，
∴3+3m＝1，
解得m＝﹣，
∴c和d的关系式为d﹣c＝1；
（2）依题意有，
①+②，得b+d+（a+c）m＝2⑤，
把③④代入⑤，得4m+4+12m＝2，即16m＝﹣2，
∴m＝﹣，
①﹣②，得b﹣d＝（c﹣a）m
即b﹣d＝﹣（c﹣a）
∵a＜c．即c﹣a＞0
∴b﹣d＝﹣（c﹣a）＜0
∴b＜d．
【点评】本题考查了二元一次方程的解、多元一次方程组的相关知识．本题的（1）比较简单，列出方程组，确定m的值并通过整体思想得到b﹣d的正负是解决（2）的关键．
6．我们用[a]表示不大于a的最大整数，例如：[2.5]＝2，[3]＝3，[﹣2.5]＝﹣3，用＜a＞表示大于a的最小整数．例如：＜2.5＞＝3，＜4＞＝5，＜﹣1.5＞＝﹣1．解决下列问题：
（1）[﹣2.6]＝　﹣3　，＜6.2＞＝　7　．
（2）已知x，y满足方程组，则[x]＝　﹣1　，＜y＞＝　3　，x的取值范围是　﹣1≤x＜0　，y的取值范围是　2≤y＜3　．
【分析】（1）根据题目所给信息求解；
（2）先求出[x]和＜y＞的值，然后求出x和y的取值范围．
【解答】解：（1）由题意得：[﹣2.6]＝﹣3，＜6.2＞＝7；
故答案为：﹣3，7；
（2）解方程组得：，
故x，y的取值范围分别为﹣1≤x＜0，2≤y＜3．
故答案为：﹣1，3，﹣1≤x＜0，2≤y＜3．
【点评】本题考查了二元一次方程组的解，解答本题的关键是读懂题意，根据题目所给的信息进行解答．
7．已知关于x、y的方程组的解满足x+y＝2，求k的值．
【分析】根据等式的性质，可得答案．
【解答】解：①×3+②得：7x+7y＝10k+4，
7（x+y）＝10k+4，
x+y＝，
x+y＝2，
＝2，
解得k＝1．
【点评】本题考查了二元一次方程组的解，利用等式的性质得出x+y＝是解题关键．
8．已知代数式kx+b，当x＝﹣3，x＝2时，代数式的值分别是1和11，求代数式的值为﹣3时，x的值．
【分析】将x＝﹣3、y＝1和x＝2、y＝11代入得关于k、b的方程组，解方程组后代入解答即可得；
【解答】解：将x＝﹣3、y＝1和x＝2、y＝11代入得：，
解得：，
把k＝2，b＝7，y＝﹣3代入y＝kx+b中，可得：﹣3＝2x+7，
解得：x＝﹣5．
【点评】本题考查的是二元一次方程组的解法，方程组中未知数的系数较小时可用代入法，当未知数的系数相等或互为相反数时用加减消元法较简单．
9．在解方程组时，由于粗心，甲看错了方程组中的a，而得到解为，乙看错了方程组中的b，而得到解为．
（1）求正确的a，b的值；
（2）求原方程组的解．
【分析】（1）把代入方程组的第二个方程，把代入方程组的第一个方程，即可得到一个关于a，b的方程组，即可求解；
（2）把a，b的值代入原方程组，然后解方程组即可．
【解答】解：（1）：将代入方程4x﹣by＝1得b＝5
将代入方程ax+5y＝﹣17得a＝4
（2）将a＝4，b＝5代入原方程组得
，
解此方程组得
【点评】本题主要考查了方程组的解的定义，正确解方程组是解题的关键．
10．解方程组：
【分析】方程组利用加减消元法求出解即可．
【解答】解：
①+②得：4x+3z＝18④，
①+③得：2x﹣2z＝2⑤
⑤×2﹣④得：﹣7z＝﹣14，
解得：z＝2，
把z＝2代入①得：x＝3，
把x＝3，z＝2代入①得：y＝1，
则方程组的解为．
【点评】此题考查了解三元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
11．已知和是关于x，y的二元一次方程y＝kx+b的解，求k，b的值．
【分析】代入后得出一个二元一次方程组，求出方程组的解即可．
【解答】解：根据题意得：，
②﹣①得：5k＝15，
解得：k＝3，
把k＝3代入①得：﹣6+b＝﹣8，
解得：b＝﹣2，
答：k＝3，b＝﹣2．
【点评】本题考查了二元一次方程的解和解二元一次方程组，能得出关于k、b的方程组是解此题的关键．
12．已知方程组和的解相同，求代数式（4a﹣3b）2018的值．
【分析】联立不含a与b的方程组成方程组，求出x与y的值，代入剩下的方程求出a与b的值，代入原式计算即可求出值．
【解答】解：联立得：，
①+②得：9x＝9，
解得：x＝1，
把x＝1代入①得：y＝﹣5，
把代入得：，
解得：a＝b＝﹣1，
则原式＝1．
【点评】此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程都成立的未知数的值．
13．解方程组
（1）
（2）
【分析】（1）方程组利用加减消元法求出解即可；
（2）方程组利用加减消元法求出解即可．
【解答】解：（1），
①+②得：2x＝6，
解得：x＝3，
把x＝3代入①得：y＝﹣1，
则方程组的解为；
（2），
①+②得：3x﹣y＝3④，
①+③得：4x＝6，
解得：x＝1.5，
把x＝1.5代入④得：y＝1.5，
把x＝1.5，y＝1.5代入①得：z＝3.5，
则方程组的解为．
【点评】此题考查了解二元一次方程组，以及解三元一次方程组，熟练掌握运算法则是解本题的关键．
14．对于任意实数a，b，定义关于“?”的一种运算如下：a?b＝2a+b．例如3?4＝2×3+4＝10．
（1）求2?（﹣5）的值；
（2）若x?（﹣y）＝2，且2y?x＝﹣1，求x+y的值．
【分析】（1）依据关于“?”的一种运算：a?b＝2a+b，即可得到2?（﹣5）的值；
（2）依据x?（﹣y）＝2，且2y?x＝﹣1，可得方程组，即可得到x+y的值．
【解答】解：（1）∵a?b＝2a+b，
∴2?（﹣5）＝2×2+（﹣5）＝4﹣5＝﹣1；
（2）∵x?（﹣y）＝2，且2y?x＝﹣1，
∴，
解得，
∴x+y＝﹣＝．
【点评】本题主要考查解二元一次方程组以及有理数的混合运算的运用，根据题意列出方程组是解题的关键．
15．解方程组：
（1）2x﹣y＝x+y＝3；
（2）．
【分析】（1）方程组变形为一般式，再利用加减消元法求解可得；
（2）利用换元法求解可得．
【解答】解：（1）由题意得，
①+②，得：3x＝6，
解得：x＝2，
将x＝2代入②，得：2+y＝3，
解得：y＝1，
则方程组的解为；
（2）令x+y＝m、x﹣y＝n，
则，
①×8﹣②，得：n＝46，
解得：n＝6，
将n＝6代入①，得：+2＝6，
解得：m＝8，
则，
③+④，得：2x＝14，
解得：x＝7，
③﹣④，得：2y＝2，
解得：y＝1，
所以原方程组的解为．
【点评】本题考查了二元一次方程组的解法．解二元一次方程组的基本思想是消元，消元的方法有代入法和加减法．如果题目没有明确指出运用什么方法解方程组，那么需要根据方程组的特点灵活选用解法．一般说来，当方程组中有一个方程的未知数的系数的绝对值是1或常数项是0时，运用代入法求解，除此之外，选用加减法求解，将会使计算较为简便．
16．解关于x、y方程组可以用（1）×2+（2）消去未知数x；也可以用（1）+（2）×5消去未知数y；求m、n的值．
【分析】根据题中消去x与y的过程，确定出m与n的值即可．
【解答】解：由题意得：，
解得：m＝﹣23，n＝﹣39．
【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
17．已知关于x，y的方程组的解满足x+2y＝2．
（1）求m的值；
（2）若a≥m，化简：|a+1|﹣|2﹣a|．
【分析】（1）根据二元一次方程组的解法即可求出答案．
（2）根据绝对值的性质即可求出答案．
【解答】解：（1）∵
∴①﹣②得：2（x+2y）＝m+1
∵x+2y＝2，
∴m+1＝4，
∴m＝3，
（2）∵a≥m，即a≥3，
∴a+1＞0，2﹣a＜0，
∴原式＝a+1﹣（a﹣2）＝3
【点评】本题考查二元一次方程组的解法，解题的关键是熟练运用方程组的解法以及绝对值的性质，本题属于基础题型．
18．（1）阅读以下内容：
已知实数x，y满足x+y＝2，且求k的值．
三位同学分别提出了以下三种不同的解题思路：
甲同学：先解关于x，y的方程组，再求k的值．
乙同学：先将方程组中的两个方程相加，再求k的值．
丙同学：先解方程组，再求k的值．
（2）你最欣赏（1）中的哪种思路？先根据你所选的思路解答此题，再对你选择的思路进行简要评价．
（评价参考建议：基于观察到题目的什么特征设计的相应思路，如何操作才能实现这些思路、运算的简洁性，以及你依此可以总结什么解题策略等等）
【分析】选择乙同学的解题思路，①+②得出5x+5y＝7k+4，求出x+y＝＝2，即可求出答案．
【解答】解：我最欣赏（1）中的乙同学的解题思路，
，
①+②得：5x+5y＝7k+4，
x+y＝，
∵x+y＝2，
∴＝2，
解得：k＝，
评价：甲同学是直接根据方程组的解的概念先解方程组，得到用含k的式子表示x，y的表达式，再代入x+y＝2得到关于k的方程，没有经过更多的观察和思考，解法比较繁琐，计算量大；
乙同学观察到了方程组中未知数x，y的系数，以及与x+y＝2中的系数的特殊关系，利用整体代入简化计算，而且不用求出x，y的值就能解决问题，思路比较灵活，计算量小；
丙同学将三个方程做为一个整体，看成关于x，y，k的三元一次方程组，并且选择先解其中只含有两个未知数x，y的二元一次方程组，相对计算量较小，但不如乙同学的简洁、灵活．
【点评】本题考查了解二元一次方程组的应用，能选择适当的方法解方程组是解此题的关键．
19．根据要求，解答下列问题．
（1）解下列方程组（直接写出方程组的解即可）：
A. B. C.
方程组A的解为　　，方程组B的解为　　，方程组C的解为　　；
（2）以上每个方程组的解中，x值与y值的大小关系为　x＝y　；
（3）请你构造一个具有以上外形特征的方程组，并直接写出它的解．
【分析】（1）分别求出三个方程组的解即可；
（2）观察三个方程组的解，找出x与y的关系即可；
（3）仿照以上外形特征写出方程组，并写出解即可．
【解答】解：（1）方程组A的解为，方程组B的解为，方程组C的解为；
故答案为：；；；
（2）以上每个方程组的解中，x值与y值的大小关系是x＝y；
故答案为：x＝y；
（3）根据题意举例为：，其解为．
【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
20．根据要求，解答下列问题．
（1）解方程组：．
（2）解下列方程组，只写出最后结果即可：①；②．
（3）以上每个方程组的解中，x值与y值有怎样的大小关系？
（4）观察以上每个方程组的外形特征，请你构造一个具有此特征的方程组，并用（3）中的结论快速求出其解．
【分析】（1）方程组利用加减消元法求出解即可；
（2）分别求出两个方程组的解即可；
（3）观察得到x与y的关系即可；
（4）写出满足此特征的方程组，把x＝y代入任何一个方程求出解即可．
【解答】解：（1），
①×2﹣②得：3y＝3，即y＝1，
把y＝1代入①得：x＝1，
则方程组的解为；
（2）①；②；
（3）以上每个方程组的解中，x＝y；
（4）
把x＝y代入①得：3y+7y＝10，即y＝1，
则方程组的解为．
【点评】此题考查了解二元一次方程组，以及二元一次方程组的解，熟练掌握运算法则是解本题的关键．
21．《九章算术》是中国古代的数学专著，下面这道题是《九章算术》中第七章的一道题：“今有共买物，人出八，盈三；人出七，不足四，问人数，物价各几何？”译文：“几个人一起去购买物品，如果每人出8钱，则多了3钱；如果每人出7钱，则少了4钱，求有多少人，物品的价格是多少”．
【分析】根据题意可以找出题目中的等量关系，列出相应的方程组，就可以解答本题．
【解答】解：设有x人，物品价格为y钱，
由题意可得，，
解得：，
答：有7人，物品的价格是53钱．
【点评】本题考查由实际问题抽象出二元一次方程组，解答本题的关键是明确题意，列出相应的方程组．
22．某服装店用4400元购进A，B两种新式服装，按标价售出后可获得毛利润2800元（毛利润＝售价﹣进价），这两种服装的进价，标价如表所示．
类型价格
　A型
　B型
　进价（元/件）
　60
　100
　标价（元/件）
　100
　160
（1）请利用二元一次方程组求这两种服装各购进的件数；
（2）如果A种服装按标价的9折出售，B种服装按标价的8折出售，那么这批服装全部售完后，服装店比按标价出售少收入多少元？
【分析】（1）设购进A种服装x件，购进B种服装y件，根据总价＝单价×数量结合总利润＝单件利润×销售数量，即可得出关于x、y的二元一次方程组，解之即可得出结论；
（2）根据少获得的总利润＝单件少获得的利润×销售数量，即可求出结论．
【解答】解：（1）设购进A种服装x件，购进B种服装y件，
根据题意得：，
解得：．
答：购进A种服装40件，购进B种服装20件．
（2）40×100×（1﹣0.9）+20×160×（1﹣0.8）＝1040（元）．
答：服装店比按标价出售少收入1040元．
【点评】本题考查了二元一次方程组的应用，解题的关键是：（1）找准等量关系，正确列出二元一次方程组；（2）根据数量关系，列式计算．
23．
如图为地铁调价后的计价表．调价后小明、小伟从家到学校乘地铁分别需要4元和3元．由于刷卡坐地铁有优惠，因此，他们平均每次实付3.6元和2.9元．已知小明从家到学校乘地铁的里程比小伟从家到学校的里程多5km，且小明每千米享受的优惠金额是小伟的2倍，求小明和小伟从家到学校乘地铁的里程分别是多少千米？
【分析】设小明和小伟从家到学校乘地铁的里程分别是x千米、y千米，题中有两个等量关系：小明从家到学校乘地铁的里程﹣小伟从家到学校的里程＝5，小明每千米享受的优惠金额＝小伟每千米享受的优惠金额×2，依此列出方程组，解方程组即可．
【解答】解：设小明和小伟从家到学校乘地铁的里程分别是x千米、y千米，根据题意得
，解得．
答：小明和小伟从家到学校乘地铁的里程分别是10千米、5千米．
【点评】本题考查了二元一次方程组的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程组，再求解．利用二元一次方程组求解的应用题一般情况下题中要给出2个等量关系，准确的找到等量关系并用方程组表示出来是解题的关键．
24．小阳骑车和步行的速度分别为240米/分钟和80米/分钟，小红每次从家步行到学校所需时间相同．请根据两人的对话解决如下问题：小阳：“如果我骑车，你步行，那么我从家到学校比你少用4分钟”小红：“如果我们俩都步行，那么从家到学校我比你少用2分钟．”若设小阳从家到学校的路程为x米，小红从家到学校所需的时间为y分钟．
（1）小阳从家到学校骑车的时间是　　分钟，步行的时间是　　分钟（用含x的式子表示）．
（2）求x，y的值．
【分析】（1）小阳从家到学校的骑车时间＝路程÷骑车速度；步行时间＝路程÷步行速度；
（2）小阳同学从家到学校的路程为x米，小红从家到学校所需时间是y分钟，由题意得：小阳步行所用时间﹣2＝小红步行所用时间；小阳骑车所用时间+4＝小红步行所用时间，由等量关系列出方程组，解方程组可得答案．
【解答】解：（1）小阳从家到学校的骑车时间是：；
步行时间是：；
故答案为：；；
（2）设小阳同学从家到学校的路程为x米，小红从家到学校所需时间是y分钟，由题意得：
，
解得：．
答：x和y的值分别是720，7．
【点评】此题主要考查了二元一次方程组的应用，关键是理解题意，表示出小明与小红步行与骑车从家到学校所用的时间，再根据题目中的等量关系列出方程组即可．
25．[阅读?领会]
怎样判断两条直线是否平行？
如图①，很难看出直线a、b是否平行，可添加“第三条线”（截线c），把判断两条直线的位置关系转化为判断两个角的数量关系．我们称直线c为“辅助线”．
在部分代数问题中，很难用算术直接计算出结果，于是，引入字母解决复杂问题，我们称引入的字母为“辅助元素”
事实上，使用“辅助线”、“辅助元”等“辅助元素”可以更容易地解决问题
【实践?体悟】
（1）计算（2+++）（+++）﹣（++）（2++++），这个算式直接计算很麻烦，请你引入合适的“辅助元”完成计算
（2）如图②，已知∠C+∠E＝∠EAB，求证AB∥CD，请你添加适当的“辅助线”，并完成证明
【创造?突破】
（3）若关于xy的方程组的解是的解是?则关于x、y的方程组的解为　x＝1，y＝﹣3．　
（4）如图③∠A1＝∠A5＝120°，∠A2＝∠A4＝70°，∠A6＝∠A8＝90°，我们把大于平角的角称为“优角”，若优角∠A3＝270°，则优角∠A7＝　250°　
【分析】（1）设a＝++，将式子进行变形，即可求解；
（2）延长BA交CE于点F，利用平行线的判定定理可得出结论；
（3）把代入方程组得到不含x，y的方程组，通过与方程组比较便可得到答案；
（4）连接A3、A7，分成两个五边形，利用多边形的内角和进行求解即可得到答案．
【解答】解：（1）设a＝++，
原式＝（2+a）（a+）﹣a（2+a+）
＝；
（2）延长BA交CE于点F，如图所示：
∵∠EAB是△EFA的外角，
∴∠EAB＝∠E+∠EFA，
又∵∠EAB＝∠E+∠C，
∴∠EFA＝∠C，
∴AB∥CD；
（3）把代入方程组得：，
与方程组比较得：，
方程组的解为：；
故答案为：x＝1，y＝﹣3．
（4）连接A7、A3，
∵五边形的内角和为（5﹣2）×180°＝540°，
∴∠A1+∠A2+∠A8+∠1+∠3＝540°，
∠A4+∠A5+∠A6+∠2+∠4＝540°，
∵∠A1＝∠A5＝120°，∠A2＝∠A4＝70°，∠A6＝∠A8＝90°，
∴∠1+∠3＝∠2+∠4＝260°，
∴∠1+∠3+∠2+∠4＝520°，
∵优角∠A3＝270°，即∠3+∠4＝270°
∴∠1+∠2＝520°﹣270°＝250°．
故答案为：250°．
【点评】本题考查了有理数的计算、方程组的求解、多边形的内角和等知识点．理解“辅助元素”并运用辅助元素是解决本题的关键．
26．七（1）班五位同学参加学校举办的数学素养党赛试卷中共有20道题，规定每题答对得5分，答错扣2分，未答得0分．赛后A，B，C，D，E五位同学对照评分标准回忆并记录了自己的答题情况（E同学只记得有7道題未答），具体如下表：
参赛同学
答对题数
答错题数
未答题数
A
19
0
1
B
17
2
1
C
15
2
3
D
17
1
2
E
/
/
7
最后从公布的竞赛成绩中获知A，B，C，D，E五位同学的实际成绩分别是95分，81分，57分，83分，58分
（1）求E同学的答对题数和答错题数；
（2）若A，B，C，D四位同学中有一位同学记错了自己的答题情况．请指出哪位同学记错了，并写出他的实际答题情况．
【分析】（1）设E同学的答对题数为x条，则答错y条．构建方程组即可解决问题；
（2）根据条件分别求出A，B，C，D的成绩即可判断；
【解答】解：（1）设E同学的答对题数为x条，则答错y条．
由题意
解得
答：设E同学的答对题数为12条，则答错1条．
（2）C同学错了自己的答题情况．应该是对13题，错4题，没有答3题．
【点评】本题考查二元一次方程组的应用，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考常考题型．
27．某公司以每吨600元的价格收购了100吨某种药材，若直接在市场上销售，每吨的售价是1000元，该公司决定加工后再出售，相关信息如下表所示：
工艺
每天可加工药材的吨数
成品率
成品售价
粗加工
14
80%
6000
精加工
6
60%
11000
（注：①成品率80%指加工100吨原料能得到80吨可销售药材；②加工后的废品不产生效益）
受市场影响，该公司必须在10天内将这批药材加工完毕．
（1）若全部粗加工，可获利　42000　元；
（2）若尽可能多的精加工，剩余的直接在市场上销售，可获利　37600　元；
（3）若部分粗加工，部分精加工，恰好10天完成，求可获利多少元？
【分析】（1）根据利润＝粗加工销售所得﹣成本求得即可；
（2）根据利润＝细加工销售所得﹣成本求得即可；
（3）设精加工x天，粗加工y天，根据题意列出关于x和y的方程组，解方程组即可．
【解答】解：（1）全部粗加工共可售得6000×80%×100＝480000（元），
成本为600×100＝60000（元），
获利为480000﹣60000＝420000（元）．
全部粗加工可获利420000元．
故答案为420000；
（2）10天共可精加工10×6＝60（吨），
可售得60×60%×11000+40×1000＝436000（元），
获利为436000﹣60000＝376000（元）．
可获利376000元，
故答案为376000；
（3）设精加工x天，粗加工y天，
则
解得，
销售可得：30×60%×11000+70×80%×6000＝534000（元），
获利为534000﹣60000＝474000（元），
答：可获利474000元．
【点评】本题考查了二元一次方程组的应用，解题的关键是：找准等量关系，正确列出二元一次方程组是解题的关键．
28．在我市“精准扶贫”工作中，甲、乙两个工程队先后接力为扶贫村庄修建一条210米长的公路，甲队每天修建15米，乙队每天修建25米，一共用10天完成．
根据题意，小红和小芳同学分别列出了下面尚不完整的方程组：
小红：小芳：
（1）请你分别写出小红和小芳所列方程组中未知数x，y表示的意义：
小红：x表示　甲队修建的天数　，y表示　乙队修建的天数　；
小芳：x表示　甲队修建的长度　，y表示　乙队修建的长度　；
（2）在题中“（　　）”内把小红和小芳所列方程组补充完整；
（3）甲工程队一共修建了　4　天，乙工程队一共修建了　150　米．
【分析】（1）根据题意和小红和小芳列出的方程组可以解答本题；
（2）、（3）利用小刚列出的方程组可以解答本题
【解答】解：（1）由题意可得，小红：x表示甲队修建的天数，y表示乙队修建的天数；
小芳：x表示甲队修建的长度，y表示乙队修建的长度；
故答案是：甲队修建的天数；乙队修建的天数；甲队修建的长度；乙队修建的长度．
（2）依题意得：小红：，
小芳：．
（3）解方程组，得
则25y＝25×6＝150（米）
即：甲工程队一共修建了 4天，乙工程队一共修建了 150米．
故答案是：4；150．
【点评】本题考查二元一次方程组的应用，解答本题的关键是明确题意，列出相应的方程组，利用方程的思想解答．
29．春天来了，石头城边，秦淮河畔，鸟语花香，柳条飘逸．为给市民提供更好的休闲锻炼环境，决定对一段总长为1800米的外秦淮河沿河步行道出新改造，该任务由甲、乙两工程队先后接力完成．甲工程队每天改造12米，乙工程队每天改造8米，共用了200天．
（1）根据题意，小莉、小刚两名同学分别列出了尚不完整的方程组如下：
小莉：小刚：
根据两名同学所列的方程组，请你分别指出未知数x、y表示的意义，然后补全小莉、小刚两名同学所列的方程组：
小莉：x表示　甲工程队改造天数　，y表示　乙工程队改造天数　；
小刚：x表示　甲工程队改造的长度　，y表示　乙工程队改造的长度　；
（2）求甲、乙两工程队分别出新改造步行道多少米．
【分析】（1）根据题意和小莉和小刚列出的方程组可以解答本题；
（2）利用小刚列出的方程组可以解答本题．
【解答】解：（1）由题意可得，
小莉的：设甲工程队改造x天，乙工程队改造y天，
，
小刚的：设甲工程队改造长度x米，乙工程队改造长度y米，
，
故答案为：200、1800；1800、200；
甲工程队改造天数，乙工程队改造天数；
甲工程队改造的长度，乙工程队改造的长度；
（2）设甲工程队改造长度x米，乙工程队改造长度y米，
，
解得，，
答：甲、乙两工程队分别出新改造步行道600米、1200米．
【点评】本题考查二元一次方程组的应用，解答本题的关键是明确题意，列出相应的方程组，利用方程的思想解答．
30．小明是一个乐思好问的学生，在解答七年级下册教材中一道拓广探索题时遇到了困难．这道题是这样的：
一个长方形的长减少5cm，宽增加2cm，就成为一个正方形，并且这两个图形的面积相等．这个长方形的长、宽各是多少？
（1）如图，设长方形的长、宽各是xcm，ycm，小明绞尽脑汁列出了三个不同的方程组：
①，②，③
以上三个方程组中，能正确反映题意的有　①②③　．（请直接填写序号）
（2）小明列出的方程，根据目前知识不易求解，便请教老师，老师提示这个问题可以列二元一次方程组来解答，并适时点拨，小明终于明白了．请你写出小明列出的二元一次方程组，并写出解题过程．
【分析】根据长﹣5＝宽+2，就成为一个正方形，及两图形的面积相等，可得出方程组①②③．
【解答】解：（1）解：由题意得：．

故答案为：①②③
（2）设长方形的长、宽各是x cm，y cm，由题意列方程组，
得
解这个方程组，得
答：长方形的长、宽分别是cm、cm．
【点评】本题考查了由实际问题抽象二元一次方程组的知识，解答本题的关键是仔细审题，找到等量关系．
31．某公司要把一批货物运往A地，准备租用汽车运输公司的甲乙两种货车．过去曾两次租用这两种货车的情况如表：
第一次
第二次
租用甲种货车（辆）
2
5
租用乙种货车（辆）
3
6
合计运货吨数（吨）
15.5
35
现租用该公司甲种货车3辆，乙种货车5辆，正好运完这批货，如果每吨货物的运费为30元，这批货物应该付运费多少元？
【分析】根据题意和表格可以得到相应的方程组，从而可以求得甲乙货车每辆可以运输多少吨货物，从而可以解答本题．
【解答】解：设甲种货车每辆运x吨，乙种货车每辆运y吨，
，得，
∴3x+5y＝3×4+5×2.5＝24.5，
30×24.5＝735（元），
答：如果每吨货物的运费为30元，这批货物应该付运费735元．
【点评】本题考查二元一次方程组的应用，解答本题的关键是明确题意，列出相应的方程组．
32．某校组织七年级全体师生乘旅游客车前往广州开展研学旅行活动．旅游客车有大小两种，2辆大客车与3辆小客车全部坐满可乘载195人，4辆大客车与2辆小客车全部坐满可乘载250人，全体师生刚好坐满12辆大客车与10辆小客车，问该校七年级师生共有多少人？
【分析】设1辆大客车乘载x人，1辆小客车乘载y人，根据“2辆大客车与3辆小客车全部坐满可乘载195人，4辆大客车与2辆小客车全部坐满可乘载250人”列出方程组并解答，最后由“全体师生刚好坐满12辆大客车与10辆小客车”求得答案．
【解答】解：设1辆大客车乘载x人，1辆小客车乘载y人，
根据题意列出方程组得：，
解得
12×45+10×35＝890（人）．
答：该校七年级师生共有890人．
【点评】此题主要考查了二元一次方程组的应用，关键是正确理解题意，找出题目中的等量关系，列出二元一次方程或方程组．
33．《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．它的代数成就主要包括开放术、正负术和方程术．其中，方程术是《九章算术》最高的数学成就．《九章算术》中记载：“今有牛五、羊二，直金十两；牛二、羊五，直金八两．问牛、羊各直金几何？”
译文：“假设有5头牛、2只羊，值金10两；2头牛、5只羊，值金8两．问每头牛、每只羊各值金多少两？”
【分析】设每头牛值金x两，每只羊各值金y两，根据“假设有5头牛、2只羊，值金10两；2头牛、5只羊，值金8两”，得到等量关系，即可列出方程组．
【解答】解：设每头牛值金x两，每只羊各值金y两．
根据题意得：
解得：
答：每头牛值金两，每头羊值金两．
【点评】本题考查了二元一次方程组的应用，解决本题的关键是找到题目中所存在的等量关系．
34．某运动员在一场篮球比赛中的技术统计如表所示：
技术
上场时间
（分钟）
出手投篮
（次）
投中
（次）
罚球得分
篮板
（个）
助攻
（次）
个人总得分
数据
46
66
22
10
11
8
60
注：表中出手投篮次数和投中次数均不包括罚球．投篮投不中不得分，罚球投中一球得1分，除罚球外投中一球得2分或3分．
根据以上信息，求本场比赛中该运动员投中2分球和3分球各几个．
【分析】设本场比赛中该运动员投中2分球x个，3分球y个，根据投中22次、罚球得分10分及本场个人得60分，即可得出关于x、y的二元一次方程组，解之即可得出结论．
【解答】解：设本场比赛中该运动员投中2分球x个，3分球y个，
根据题意得：，
解得：．
答：本场比赛中该运动员投中2分球16个，3分球6个．
【点评】本题考查了二元一次方程组的应用，找准等量关系，正确列出二元一次方程组是解题的关键．
35．分别用8个大小一样的长方形拼图．如图①，小明拼成了一个大的长方形；如图②，小红拼成了一个大的正方形，但中间恰好空出一个边长为1mm的小正方形．你能求出小长方形的长和宽吗？
【分析】设小长方形的长为xmm，宽为ymm，观察图①、图②，可得出关于x、y的二元一次方程组，解之即可得出结论．
【解答】解：设小长方形的长为xmm，宽为ymm，
根据题意得：，
解得：．
答：小长方形的长为5mm，宽为3mm．
【点评】本题考查了二元一次方程组的应用，找准等量关系，正确列出二元一次方程组是解题的关键．
36．我国古代数学著作《九章算术》中有这样一题，原文是：“今有大器五小器一容三斛，大器一小器五容二斛，问大小器各容几何．”意思是：有大小两种盛酒的桶，已知5个大桶加上1个小桶可以盛酒3斛（斛，是古代的一种容量单位），1个大桶加上5个小桶可以盛酒2斛．1个大桶、1个小桶分别可以盛酒多少斛？请解答．
【分析】直接利用5个大桶加上1个小桶可以盛酒3斛，1个大桶加上5个小桶可以盛酒2斛，分别得出等式组成方程组求出答案．
【解答】解：设1个大桶可以盛酒x斛，1个小桶可以盛酒y斛，
则，
解得：，
答：1个大桶可以盛酒斛，1个小桶可以盛酒斛．
【点评】此题主要考查了二元一次方程组的应用，正确得出等量关系是解题关键．
37．在国家积极推进“互联网+”行动以来，网上购物已成为生活中的新常态．某甲在网购平台上购买商品A、B共三次，只有一次购买时，商品A、B同时打折，其余两次均按标价购买，三次购买商品A、B的数量和费用如下表：
购买商品A的数量（个）
购买商品B的数量（个）
购买总费用（元）
第一次购物
6
4
240
第二次购物
8
6
204
第三次购物
5
6
280
（1）某甲第　二　次购物时，商品A、B同时打折，并简略叙述理由．
理由为：　∵某甲在某商店购买商品A、B共三次，只有一次购买时，商品A、B同时打折，其余两次均按标价购买，且只有第二次购买数量明显增多，但是总的费用不高，
∴某甲以折扣价购买商品A、B是第二次购物　．
（2）请求出商品A的标价．
【分析】（1）根据图表可得某甲以折扣价购买商品A、B是第二次购物；
（2）设商品A的标价为x元，商品B的标价为y元，根据图表列出方程组求出x和y的值即可．
【解答】解：（1）某甲以折扣价购买商品A、B是第二次购物．
理由：∵某甲在某商店购买商品A、B共三次，只有一次购买时，商品A、B同时打折，其余两次均按标价购买，且只有第二次购买数量明显增多，但是总的费用不高，
∴某甲以折扣价购买商品A、B是第二次购物；
（2）设商品A的标价为x元，商品B的标价为y元，
根据题意，得，
解得：．
答：商品A的标价为20元．
故答案为：二；∵某甲在某商店购买商品A、B共三次，只有一次购买时，商品A、B同时打折，其余两次均按标价购买，且只有第二次购买数量明显增多，但是总的费用不高，∴某甲以折扣价购买商品A、B是第二次购物．
【点评】本题考查了二元一次方程组和一元一次方程的应用，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程求解．
38．随着“互联网+”时代的到来，一种新型打车方式受到大众欢迎，该打车方式的总费用由里程费和耗时费组成，其中里程费按x元/公里计算，耗时费按y元/分钟计算（总费用不足9元按9元计价）．小明、小刚两人用该打车方式出行，按上述计价规则，其打车总费用、行驶里程数与打车时间如表：
时间（分钟）
里程数（公里）
车费（元）
小明
8
8
12
小刚
12
10
16
（1）求x，y的值；
（2）如果小华也用该打车方式，打车行驶了11公里，用了14分钟，那么小华的打车总费用为多少？
【分析】（1）根据表格内的数据结合打车费＝里程费×里程+耗时费×耗时，即可得出关于x、y的二元一次方程组，解之即可得出结论；
（2）根据打车费＝里程费×里程+耗时费×耗时，列式计算即可求出结论．
【解答】解：（1）根据题意得：，
解得：．
（2）11×1+14×＝18（元）．
答：小华的打车总费用是18元．
【点评】本题考查了二元一次方程组的应用，解题的关键是：（1）找准等量关系，正确列出二元一次方程组；（2）根据数量间的关系，列式计算．
39．某市为了鼓励居民节约用水，决定实行两级收费制度，若每月用水量不超过14吨（含14吨），则每吨按政府补贴优惠价m元收费；若每月用水量超过14吨，则超过部分每吨按市场价n元收费．小明家3月份用水20吨，交水费49元；4月份用水18吨，交水费42元．
（1）求每吨水的政府补贴优惠价m和市场价n分别是多少元？
（2）小明家5月份交水费70元，则5月份他家用了多少吨水？
【分析】（1）根据“小明家3月份用水20吨，交水费49元；4月份用水18吨，交水费42元”，即可得出关于m、n的二元一次方程组，解之即可得出结论；
（2）设5月份小明家用了x吨水，根据应交水费＝2×14+3.5×超出14吨的部分，即可得出关于x的一元一次方程，解之即可得出结论．
【解答】解：（1）根据题意得：，
解得：．
答：每吨水的政府补贴优惠价m是2元，市场价n是3.5元．
（2）设5月份小明家用了x吨水，
根据题意得：14×2+3.5（x﹣14）＝70，
解得：x＝26．
答：5月份小明家用了26吨水．
【点评】本题考查了二元一次方程组的应用以及一元一次方程的应用，解题的关键是：（1）找准等量关系，正确列出二元一次方程组；（2）找准等量关系，正确列出一元一次方程．
40．奖励在演讲比赛中获奖的同学，班主任派学习委员小明为获奖同学买奖品，要求每人一件，小明到文具店看了商品后，决定奖品在钢笔和笔记本中选择，如果买4个笔记本和2支钢笔，则需86元；如果买3个笔记本和1支钢笔，则需57元．
（1）求购买每个笔记本和钢笔分别为多少元？
（2）售货员提示，买钢笔有优惠，具体方法是：如果买钢笔超过10支，那么超出部分可以享受8折优惠，若买15支钢笔，20个笔记本，一共花多少钱？
【分析】（1）设每个笔记本的价格为x元，每支钢笔的价格为y元，根据“买4个笔记本和2支钢笔，则需86元；买3个笔记本和1支钢笔，则需57元”，即可得出关于x、y的二元一次方程组，解之即可得出结论；
（2）根据总价＝单价×数量，列式计算即可得出结论．
【解答】解：（1）设每个笔记本的价格为x元，每支钢笔的价格为y元．
根据题意得：，
解得：．
答：每个笔记本的价格为14元，每支钢笔的价格为15元．
（2）10×15+（15﹣10）×15×0.8+14×20＝490（元）．
答：一共花了490元钱．
【点评】本题考查了二元一次方程组的应用，解题的关键是：（1）找准等量关系，列出二元一次方程组；（2）根据数量关系，列式计算．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布
日期：2019/3/3 7:50:07；用户：zhrasce20；邮箱：zhrasce20@163.com；学号：6322261