2.4 二元一次方程组的应用(2)同步练习
文档属性
| 名称 | 2.4 二元一次方程组的应用(2)同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-04 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2.4 二元一次方程组的应用(2)
重点提示
列方程组解应用题的一般步骤:①审:审题,找出题中的等量关系;②设:设未知数;③列:根据等量关系列出方程组;④解:解方程组;⑤验:检验方程组解的正确性及是否符合实际;⑥答:写出答案.
1.一个两位数的十位数字与个位数字之和是7,如果把这个两位数加上45,那么恰好成为把个位数字和十位数字对调后组成的数,这个两位数是( ).
A.16 B.25 C.52 D.61
2.如图所示,AB⊥BC,∠ABD的度数比∠DBC的度数的2倍少15°.设∠ABD与∠DBC的度数分别为x°,y°,根据题意,下列方程组中,正确的是( ).
A. B. C. D.
(第2题) (第3题)
3.某市举办花展,如图所示,在长为14m、宽为10m的长方形展厅中划出三个形状、大小完全一样的小长方形区域摆放水仙花,则每个小长方形区域的周长为( ).
A.8m B.13m C.16m D.20m
4.小明在学习之余去买文具,打算购买5支单价相同的签字笔和3本单价相同的笔记本,期间他与售货员对话如下:
小明:您好,我要买5支签字笔和3本笔记本. 售货员:好的,那你应该付52元. 小明:刚才我把两种文具的单价弄反了,以为要付44元.
请你判断在单价没有弄反的情况下,购买1支签字笔和1本笔记本应付( ).
A.10元 B.11元 C.12元 D.13元
5.某班级组织学生去看演出,甲种票每张24元,乙种票每张18元.如果35名学生购票恰好用去750元,那么甲种票买了 张,乙种票买了 张.
6.一批宿舍,若每间住1人,则10人无法安排入住;若每间住3人,则有10间宿舍无人住,这批宿舍有 间.
7.甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按50%的利润定价,乙服装按40%的利润定价.在实际出售时,应顾客要求,两件服装均按9折出售,这样商店共获利157元.设甲服装的成本是x元,乙服装的成本是y元,依题意列方程组得
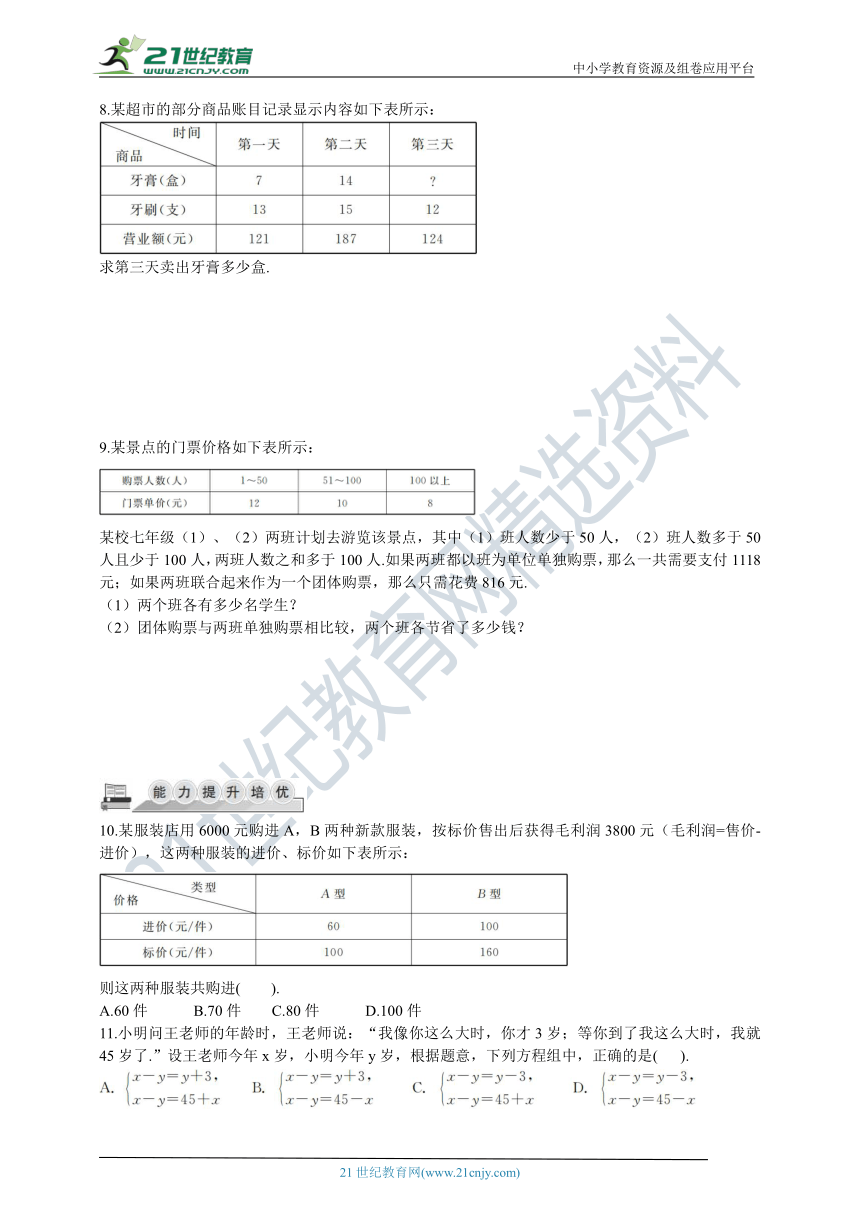
8.某超市的部分商品账目记录显示内容如下表所示:
求第三天卖出牙膏多少盒.
9.某景点的门票价格如下表所示:
某校七年级(1)、(2)两班计划去游览该景点,其中(1)班人数少于50人,(2)班人数多于50人且少于100人,两班人数之和多于100人.如果两班都以班为单位单独购票,那么一共需要支付1118元;如果两班联合起来作为一个团体购票,那么只需花费816元.
(1)两个班各有多少名学生?
(2)团体购票与两班单独购票相比较,两个班各节省了多少钱?
10.某服装店用6000元购进A,B两种新款服装,按标价售出后获得毛利润3800元(毛利润=售价-进价),这两种服装的进价、标价如下表所示:
则这两种服装共购进( ).
A.60件 B.70件 C.80件 D.100件
11.小明问王老师的年龄时,王老师说:“我像你这么大时,你才3岁;等你到了我这么大时,我就45岁了.”设王老师今年x岁,小明今年y岁,根据题意,下列方程组中,正确的是( ).
(第12题)
12.利用两块长方体木块测量一张桌子的高度.首先按图1的方式放置,再交换两木块的位置,按图2的方式放置.测量的数据如图所示,则桌子的高度是( ).
A.73cm B.74cm C.75cm D.76cm
13.如图1所示,在边长为a的大正方形中剪去一个边长为b的小正方形,再将图中的阴影部分剪拼成一个长方形,如图2所示.若这个拼成的长方形的长为30,宽为20,则图2中Ⅱ部分的面积是 .
图1 图2
(第13题) (第14题)
14.如图所示,等臂天平呈平衡状态,其中左侧托盘有一袋石头,右侧托盘有一袋石头和2个各10g的砝码.将左侧袋中的一颗石头移至右侧托盘,并拿走右侧托盘的1个砝码后,天平仍呈平衡状态.那么被移动的石头的质量为 g.
15.现安排一批工人完成一项工作,如果这批工人同时开始工作,且每个工人的工作效率相同,那么9h可以完工;如果开始先安排1人做,以后每隔t(h)(t为整数)增加1人,且每个人都一直做到工作全部完成,结果最后一个人做的时间是第1人做的时间的,那么第一人做的时间是 h.
16.为建设环境友好型社会,克服因干旱而造成的电力紧张问题,切实做好节能减排工作.某地决定对居民家庭用电实行“阶梯电价”.电力公司规定:居民家庭每月用电量在80kW·h以下(含80kW·h)时,实行“基本电价”;当居民家庭月用电量超过80kW·h时,超过部分实行“提高电价”.
(1)小张家2016年4月份用电100kW·h,上缴电费68元;5月份用电120kW·h,上缴电费88元.求“基本电价”和“提高电价”分别为每千瓦时多少元?
(2)若6月份小张家用电130kW·h,请计算小张家6月份应上缴的电费.
17.上网流量、语音通话是手机通信消费的两大主体,目前,某通信公司推出消费优惠新招——“定制套餐”,消费者可根据实际情况自由定制每月上网流量与语音通话时间,并按照两者的阶梯资费标准缴纳通信费.下表是流量与语音的阶梯定价标准.
【小提示:阶梯定价收费计算方法,如600分钟语音通话费=0.15×500+0.12×(600-500)=87元】
(1)甲定制了600MB的月流量,花费48元;乙定制了2GB的月流量,花费120.4元,求a,b的值.(注:1GB=1024MB)
(2)甲的套餐费用为199元,其中含600MB的月流量;丙的套餐费用为244.2元,其中包含1GB的月流量.两人均定制了超过1000分钟的每月语音通话时间,并且丙的语音通话时间比甲多300分钟,求m的值.
(第18题)
18.如图所示,8块相同的长方形地砖拼成一个大长方形,则每块小长方形地砖的面积是 cm2.
19.学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元.
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,且花费的总费用不超过280元.请设计出符合条件的购买方案,并说明哪种方案最省钱.
20.某商贸公司有A,B两种型号的商品需运出,这两种商品的体积和质量分别如下表所示:
(1)已知一批商品有A,B两种型号,体积一共是20m3,质量一共是10.5t,求A,B两种型号商品各有几件.
(2)物流公司可供使用的货车每辆额定载重3.5t,容积为6m3,其收费方式有以下两种:
①按车收费:每辆车运输货物到目的地收费600元;
②按吨收费:每吨货物运输到目的地收费200元.
要将(1)中的商品一次或分批运输到目的地,该商贸公司应如何选择运送付费方式才能使运费最少?求出该方式下的运费是多少元.
2.4 二元一次方程组的应用(2)
重点提示
列方程组解应用题的一般步骤:①审:审题,找出题中的等量关系;②设:设未知数;③列:根据等量关系列出方程组;④解:解方程组;⑤验:检验方程组解的正确性及是否符合实际;⑥答:写出答案.
1.一个两位数的十位数字与个位数字之和是7,如果把这个两位数加上45,那么恰好成为把个位数字和十位数字对调后组成的数,这个两位数是(A).
A.16 B.25 C.52 D.61
2.如图所示,AB⊥BC,∠ABD的度数比∠DBC的度数的2倍少15°.设∠ABD与∠DBC的度数分别为x°,y°,根据题意,下列方程组中,正确的是(B).
A. B. C. D.
(第2题) (第3题)
3.某市举办花展,如图所示,在长为14m、宽为10m的长方形展厅中划出三个形状、大小完全一样的小长方形区域摆放水仙花,则每个小长方形区域的周长为(C).
A.8m B.13m C.16m D.20m
4.小明在学习之余去买文具,打算购买5支单价相同的签字笔和3本单价相同的笔记本,期间他与售货员对话如下:
小明:您好,我要买5支签字笔和3本笔记本. 售货员:好的,那你应该付52元. 小明:刚才我把两种文具的单价弄反了,以为要付44元.
请你判断在单价没有弄反的情况下,购买1支签字笔和1本笔记本应付(C).
A.10元 B.11元 C.12元 D.13元
5.某班级组织学生去看演出,甲种票每张24元,乙种票每张18元.如果35名学生购票恰好用去750元,那么甲种票买了 20 张,乙种票买了 15 张.
6.一批宿舍,若每间住1人,则10人无法安排入住;若每间住3人,则有10间宿舍无人住,这批宿舍有 20 间.
7.甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按50%的利润定价,乙服装按40%的利润定价.在实际出售时,应顾客要求,两件服装均按9折出售,这样商店共获利157元.设甲服装的成本是x元,乙服装的成本是y元,依题意列方程组得
8.某超市的部分商品账目记录显示内容如下表所示:
求第三天卖出牙膏多少盒.
【答案】设牙膏每盒x元,牙刷每支y元.
由题意得解得
∵ 8=8(盒),∴第三天卖出牙膏8盒.
9.某景点的门票价格如下表所示:
某校七年级(1)、(2)两班计划去游览该景点,其中(1)班人数少于50人,(2)班人数多于50人且少于100人,两班人数之和多于100人.如果两班都以班为单位单独购票,那么一共需要支付1118元;如果两班联合起来作为一个团体购票,那么只需花费816元.
(1)两个班各有多少名学生?
(2)团体购票与两班单独购票相比较,两个班各节省了多少钱?
【答案】(1)设七(1)班有x名学生,七(2)班有y名学生.
由题意得解得
∴七(1)班有49名学生,七(2)班有53名学生.
(2)七(1)班节省的费用为(12-8)×49=196(元),
七(2)班节省的费用为(10-8)×53=106(元).
10.某服装店用6000元购进A,B两种新款服装,按标价售出后获得毛利润3800元(毛利润=售价-进价),这两种服装的进价、标价如下表所示:
则这两种服装共购进(C).
A.60件 B.70件 C.80件 D.100件
11.小明问王老师的年龄时,王老师说:“我像你这么大时,你才3岁;等你到了我这么大时,我就45岁了.”设王老师今年x岁,小明今年y岁,根据题意,下列方程组中,正确的是(D).
(第12题)
12.利用两块长方体木块测量一张桌子的高度.首先按图1的方式放置,再交换两木块的位置,按图2的方式放置.测量的数据如图所示,则桌子的高度是(D).
A.73cm B.74cm C.75cm D.76cm
13.如图1所示,在边长为a的大正方形中剪去一个边长为b的小正方形,再将图中的阴影部分剪拼成一个长方形,如图2所示.若这个拼成的长方形的长为30,宽为20,则图2中Ⅱ部分的面积是 100 .
图1 图2
(第13题) (第14题)
14.如图所示,等臂天平呈平衡状态,其中左侧托盘有一袋石头,右侧托盘有一袋石头和2个各10g的砝码.将左侧袋中的一颗石头移至右侧托盘,并拿走右侧托盘的1个砝码后,天平仍呈平衡状态.那么被移动的石头的质量为 5 g.
15.现安排一批工人完成一项工作,如果这批工人同时开始工作,且每个工人的工作效率相同,那么9h可以完工;如果开始先安排1人做,以后每隔t(h)(t为整数)增加1人,且每个人都一直做到工作全部完成,结果最后一个人做的时间是第1人做的时间的,那么第一人做的时间是 15 h.
16.为建设环境友好型社会,克服因干旱而造成的电力紧张问题,切实做好节能减排工作.某地决定对居民家庭用电实行“阶梯电价”.电力公司规定:居民家庭每月用电量在80kW·h以下(含80kW·h)时,实行“基本电价”;当居民家庭月用电量超过80kW·h时,超过部分实行“提高电价”.
(1)小张家2016年4月份用电100kW·h,上缴电费68元;5月份用电120kW·h,上缴电费88元.求“基本电价”和“提高电价”分别为每千瓦时多少元?
(2)若6月份小张家用电130kW·h,请计算小张家6月份应上缴的电费.
【答案】(1)设“基本电价”为x元/千瓦时,“提高电价”为y元/千瓦时.
由题意得解得
∴“基本电价”为0.6元/千瓦时,“提高电价”为1元/千瓦时.
(2)80×0.6+(130-80)×1=98(元).
17.上网流量、语音通话是手机通信消费的两大主体,目前,某通信公司推出消费优惠新招——“定制套餐”,消费者可根据实际情况自由定制每月上网流量与语音通话时间,并按照两者的阶梯资费标准缴纳通信费.下表是流量与语音的阶梯定价标准.
【小提示:阶梯定价收费计算方法,如600分钟语音通话费=0.15×500+0.12×(600-500)=87元】
(1)甲定制了600MB的月流量,花费48元;乙定制了2GB的月流量,花费120.4元,求a,b的值.(注:1GB=1024MB)
(2)甲的套餐费用为199元,其中含600MB的月流量;丙的套餐费用为244.2元,其中包含1GB的月流量.两人均定制了超过1000分钟的每月语音通话时间,并且丙的语音通话时间比甲多300分钟,求m的值.
【答案】(1)依题意得
解得∴a的值为0.15,b的值为0.05.
(2)设甲的套餐中定制x(x>1000)分钟的每月通话时间,则丙的套餐中定制(x+300)分钟的每月通话时间.
丙定制了1GB的月流量,需花费100×0.15+(500-100)×0.07+(1024-500)×0.05=69.2(元),依题意得:
②-①,得21.2+300m=45.2,解得m=0.08.∴m的值为0.08.
(第18题)
18.如图所示,8块相同的长方形地砖拼成一个大长方形,则每块小长方形地砖的面积是 300 cm2.
19.学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元.
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,且花费的总费用不超过280元.请设计出符合条件的购买方案,并说明哪种方案最省钱.
【答案】(1)设一只A型节能灯的售价是x元,一只B型节能灯的售价是y元.
根据题意得解得
∴一只A型节能灯的售价是5元,一只B型节能灯的售价是7元.
(2)设购进A型节能灯m只,总费用为W元.根据题意得W=5m+7(50-m)=-2m+350,
∵m≤3(50-m),解得m≤37.5.而m为正整数,∴m≤37.当m=37时,W=276<280,满足条件;
当m=36时,W=278<280,满足条件;当m=35时,W=280=280,满足条件;当m<35时,W>280,不满足条件.∴符合条件的购买方案有上述3种,最省钱的购买方案是购买A型灯37只,B型灯13只.
20.某商贸公司有A,B两种型号的商品需运出,这两种商品的体积和质量分别如下表所示:
(1)已知一批商品有A,B两种型号,体积一共是20m3,质量一共是10.5t,求A,B两种型号商品各有几件.
(2)物流公司可供使用的货车每辆额定载重3.5t,容积为6m3,其收费方式有以下两种:
①按车收费:每辆车运输货物到目的地收费600元;
②按吨收费:每吨货物运输到目的地收费200元.
要将(1)中的商品一次或分批运输到目的地,该商贸公司应如何选择运送付费方式才能使运费最少?求出该方式下的运费是多少元.
【答案】(1)设A型商品有x件,B型商品有y件.由题意得解得
∴A型商品有5件,B型商品有8件.
(2)①按车收费:10.5÷3.5=3(辆),6×3=18<20,∴3辆汽车不够,需要4辆车.
4×600=2400(元).②按吨收费:200×10.5=2100(元).③先用3辆车运送18 m3,剩余1件B型产品按吨付费:3×600+1×200=2000(元).∴先按车付费用3辆车运送18 m3,再按吨付费运送1件B型产品,运费最少,为2000元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
