2.4 二元一次方程组的应用(2课时)课件
文档属性
| 名称 | 2.4 二元一次方程组的应用(2课时)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-13 15:50:39 | ||
图片预览







文档简介
2.4 二元一次方程组的应用
浙教版 七年级下
新知导入
1. 解二元一次方程组的方法:
① 代入消元法
② 加减消元法
实际问题
问题解决
检验
求解
方程(组)
2. 解二元一次方程组的实质:
新知讲解
游泳池中有一群小朋友,男孩戴蓝色游泳帽,女孩戴红色游泳帽. 如果每位男孩看到蓝色与红色的游泳帽一样多, 而每位女孩看到蓝色的游泳帽比红色的多1倍,你知道男孩与女孩各有多少人吗?
要解决这一问题,我们可以从以下几个方面进
行思考:
(1) 问题中所求的未知数有几个?
(2) 有哪些等量关系?
(3) 怎样设未知数?可以列出几个方程?
(4) 本题能列一元一次方程求解吗?用列二元一次方
程组的方法求解,有什么优点?
新知讲解
游泳池中有一群小朋友,男孩戴蓝色游泳帽,女孩戴红色游泳帽. 如果每位男孩看到蓝色与红色的游泳帽一样多, 而每位女孩看到蓝色的游泳帽比红色的多1倍,你知道男孩与女孩各有多少人吗?
思考:(1)问题中所求的未知数有几个?
2个:男孩人数、女孩人数
(2)有哪些等量关系?
①男孩人数-1=女孩人数;
②男孩人数=2(女孩人数-1)
新知讲解
(3)怎样设未知数?可以列出几个方程?
解:设男孩x人,女孩y人,则由题意得,可列两个方程:
(4)本题能列一元一次方程求解吗?用列二元一次方程组的方法求解,有什么优点?
一元一次方程:设男孩x,则女孩为x-1,则x=2(x-1-1),解得x=4.
列二元一次方程组优点:使问题简单化,易找出等量关系.
新知讲解
用列二元一次方程组的方法求解应用题:
当问题中所求的未知数有两个时,
用两个字母来表示未知数往往能使问题变得简单,比较容易找出等量关系,列出方程.
要注意的是必须寻找两个等量关系,列出两个不同的方程,组成二元一次方程组.
新知讲解
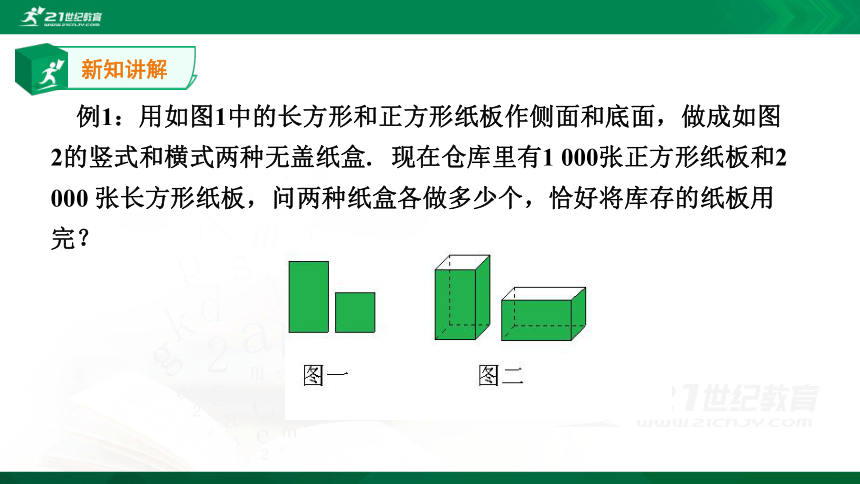
例1:用如图1中的长方形和正方形纸板作侧面和底面,做成如图 2的竖式和横式两种无盖纸盒. 现在仓库里有1 000张正方形纸板和2 000 张长方形纸板,问两种纸盒各做多少个,恰好将库存的纸板用完?
新知讲解
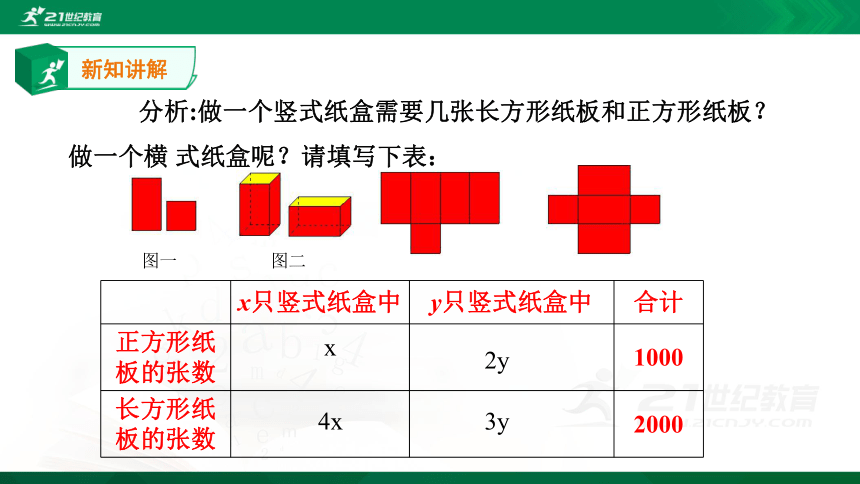
分析:做一个竖式纸盒需要几张长方形纸板和正方形纸板?做一个横 式纸盒呢?请填写下表:
x
2y
4x
3y
x只竖式纸盒中 y只竖式纸盒中 合计
正方形纸板的张数 1000
长方形纸板的张数 2000
新知讲解
解:设做竖式纸盒x个,横式纸盒y个.根据题意,得
①×4-②,得 5y=2 000, 解得y=400.
把y=400 代入①,得 x+800=1 000, 解得x=200.
经检验,这个解满足方程组,且符合题意.
答: 做竖式纸盒200个,横式纸盒400个,恰好纸板用完.
新知讲解
一般地,问题解决的基本步骤适用于二元一次方程组解决实际问题:
理解问题:审题,搞清已知和未知,分析数量关系;
制定计划:考虑如何根据等量关系设元,列出方程组;
执行计划:列出方程组并求解,得到答案;
回顾:检查和反思解题过程,检查答案的正确性以及是否符合题意.
新知讲解
例2 一根金属棒在0℃时的长度是q (m),温度每升高1℃,它就伸长p (m).当温度为t ℃时,金属棒的长度可用公式L=pt+q计算.已测得当t =100℃时,L=2.002m;当t =500℃时,L=2.01m.
(1)求p,q的值;
(2)若这根金属棒加热后长度伸长到2.016m,问这时金属棒的温度是多少?
分析:
①从所求出发,求p、q两个字母的值,必须列出几条方程?
②从已知出发,如何利用L=pt+q及两对已知量.
③在⑴题中求得字母系数p与q之后,就可以得到 L与 t 怎样的关系式?那么第⑵题中,已知 L=2.016米时,如何求 t 的值。
新知讲解
解:(1)根据题意,得
②-①,得400p=0.008
解得p=0.00002
把p=0.00002代入①,得0.002+q=2.002
解得q=2
答:p=0.00002,q=2
(2)由(1),得L=0.00002t+2
当L=2.016m时
2.016=0.00002t+2
解这个方程,得t=800
答:此时金属棒的温度是800 ℃.
新知讲解
例3 通过对一份中学生营养快餐的检测,得到以下信息:
① 快餐总质量为300 g;
② 快餐的成分:蛋白质、碳水化合物、脂肪、矿物质;
③ 蛋白质和脂肪含量占50%;矿物质的含量是脂肪
含量的2倍;蛋白质和碳水化合物含量占85%。
根据上述数据回答下面的问题:
试分别求出营养快餐中蛋白质、碳水化合物、脂肪、矿物质的质量和所占百分比;
新知讲解
解: 设一份营养快餐中含蛋白质x (g)脂肪y (g) ,则矿物质为2y (g) ,碳水化合物为(300×85%-x) (g) .
由题意,得
①+②,得 3y=45,
解得 y=15 (g).
∴ x=150-y=135 (g),
2y=2×15=30(g),
300×85%-x=255-135=120(g)
新知讲解
中学生营养快餐成分统计表
将以上中学生营养快餐成分绘制成表格如下:
中学生营养快餐成分绘制成扇形统计图如右:
蛋白质 脂肪 矿物质 碳水化合物 合计
各种成分的质量(g) 135 15 30 120 300
各种成分所占百分比 45% 5% 10% 40% 100%
新知讲解
解信息量大,关系复杂的实际问题时,要仔细分析题意,找出等量关系,利用它们的数量关系适当地设元,然后列方程组解题.
课堂练习
1、设A、B两镇相距x千米,甲从A镇、乙从B镇同时出发,相向而行,甲、乙行驶的速度分别为u千米/小时、v千米/小时,并有:【版权所
①出发后30分钟相遇;
②甲到B镇后立即返回,追上乙时又经过了30分钟;
③当甲追上乙时他俩离A镇还有4千米.求x、u、v.
根据题意,由条件③,有四位同学各得到第3个方程如下,其中错误的一个是( )
A.x=u+4 B.x=v+4 C.2x﹣u=4 D.x﹣v=4
A
课堂练习
2、养牛场原有30头大牛和15头小牛,1天约用饲料675kg,一周后又购进12头大牛和5头小牛,这时1天约用饲料940kg。饲养员李大叔估计每头大牛每天约需饲料18~20kg,每头小牛每天约需饲料7~8kg。你能通过计算检验他的估计吗?
30×每头大牛量+15×每头小牛量=675
42×每头大牛量+20×每头小牛量=940
30x+15y=675
42x+20y=940
课堂练习
30x+15y=675 ①
42x+20y=940 ②
解:设每头大牛 x kg/天,每头小牛 y kg/天,则
解:由①,得
由②,得
2x+y=45 ③
2.1x+y=47 ④
④-③
0.1x=2
x=20
把x=20代入③,得
40+y=45
y=5
答:每头大牛20kg/天,每头小牛5kg/天,李大叔对大牛的估计正确,对小牛的估计不正确。
∴方程组的解为
课堂练习
3、张大叔承包的10亩地理所种植的甲、乙两种蔬菜共获利13800元,其中甲种蔬菜每亩获利1200元,乙种蔬菜每亩获利1500元.问甲、乙两种蔬菜各种植了多少亩?
分析:题目中的等量关系非常明显:甲乙两种蔬菜共种植10亩;甲乙两种蔬菜共获利13800元。由这两个等量关系列出方程组求解即可。
课堂总结
审→设→找→列→解→验→答
(1)审:审题,分析题中已知什么,求什么,明确各数量之间的关系.
(2)设:设未知数(一般求什么,就设什么为x,y).
(3)找:找出能够表示应用题全部意义的两个等量关系.
(4)列:根据这两个等量关系列出需要的代数式,进而列出两个方程,组成方程组.
(5)解:解所列方程组,得未知数的值.
(6)验:检验所求未知数的值是 否符合题意,是否符合实际.
(7)答:写出答案(包括单位名称).
列二元一次方程组解应用题的一般步骤:
板书设计
列二元一次方程组解应用题的一般步骤:
审→设→找→列→解→验→答
作业布置
教材49页习题第1、2、5、6题。
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
浙教版 七年级下
新知导入
1. 解二元一次方程组的方法:
① 代入消元法
② 加减消元法
实际问题
问题解决
检验
求解
方程(组)
2. 解二元一次方程组的实质:
新知讲解
游泳池中有一群小朋友,男孩戴蓝色游泳帽,女孩戴红色游泳帽. 如果每位男孩看到蓝色与红色的游泳帽一样多, 而每位女孩看到蓝色的游泳帽比红色的多1倍,你知道男孩与女孩各有多少人吗?
要解决这一问题,我们可以从以下几个方面进
行思考:
(1) 问题中所求的未知数有几个?
(2) 有哪些等量关系?
(3) 怎样设未知数?可以列出几个方程?
(4) 本题能列一元一次方程求解吗?用列二元一次方
程组的方法求解,有什么优点?
新知讲解
游泳池中有一群小朋友,男孩戴蓝色游泳帽,女孩戴红色游泳帽. 如果每位男孩看到蓝色与红色的游泳帽一样多, 而每位女孩看到蓝色的游泳帽比红色的多1倍,你知道男孩与女孩各有多少人吗?
思考:(1)问题中所求的未知数有几个?
2个:男孩人数、女孩人数
(2)有哪些等量关系?
①男孩人数-1=女孩人数;
②男孩人数=2(女孩人数-1)
新知讲解
(3)怎样设未知数?可以列出几个方程?
解:设男孩x人,女孩y人,则由题意得,可列两个方程:
(4)本题能列一元一次方程求解吗?用列二元一次方程组的方法求解,有什么优点?
一元一次方程:设男孩x,则女孩为x-1,则x=2(x-1-1),解得x=4.
列二元一次方程组优点:使问题简单化,易找出等量关系.
新知讲解
用列二元一次方程组的方法求解应用题:
当问题中所求的未知数有两个时,
用两个字母来表示未知数往往能使问题变得简单,比较容易找出等量关系,列出方程.
要注意的是必须寻找两个等量关系,列出两个不同的方程,组成二元一次方程组.
新知讲解
例1:用如图1中的长方形和正方形纸板作侧面和底面,做成如图 2的竖式和横式两种无盖纸盒. 现在仓库里有1 000张正方形纸板和2 000 张长方形纸板,问两种纸盒各做多少个,恰好将库存的纸板用完?
新知讲解
分析:做一个竖式纸盒需要几张长方形纸板和正方形纸板?做一个横 式纸盒呢?请填写下表:
x
2y
4x
3y
x只竖式纸盒中 y只竖式纸盒中 合计
正方形纸板的张数 1000
长方形纸板的张数 2000
新知讲解
解:设做竖式纸盒x个,横式纸盒y个.根据题意,得
①×4-②,得 5y=2 000, 解得y=400.
把y=400 代入①,得 x+800=1 000, 解得x=200.
经检验,这个解满足方程组,且符合题意.
答: 做竖式纸盒200个,横式纸盒400个,恰好纸板用完.
新知讲解
一般地,问题解决的基本步骤适用于二元一次方程组解决实际问题:
理解问题:审题,搞清已知和未知,分析数量关系;
制定计划:考虑如何根据等量关系设元,列出方程组;
执行计划:列出方程组并求解,得到答案;
回顾:检查和反思解题过程,检查答案的正确性以及是否符合题意.
新知讲解
例2 一根金属棒在0℃时的长度是q (m),温度每升高1℃,它就伸长p (m).当温度为t ℃时,金属棒的长度可用公式L=pt+q计算.已测得当t =100℃时,L=2.002m;当t =500℃时,L=2.01m.
(1)求p,q的值;
(2)若这根金属棒加热后长度伸长到2.016m,问这时金属棒的温度是多少?
分析:
①从所求出发,求p、q两个字母的值,必须列出几条方程?
②从已知出发,如何利用L=pt+q及两对已知量.
③在⑴题中求得字母系数p与q之后,就可以得到 L与 t 怎样的关系式?那么第⑵题中,已知 L=2.016米时,如何求 t 的值。
新知讲解
解:(1)根据题意,得
②-①,得400p=0.008
解得p=0.00002
把p=0.00002代入①,得0.002+q=2.002
解得q=2
答:p=0.00002,q=2
(2)由(1),得L=0.00002t+2
当L=2.016m时
2.016=0.00002t+2
解这个方程,得t=800
答:此时金属棒的温度是800 ℃.
新知讲解
例3 通过对一份中学生营养快餐的检测,得到以下信息:
① 快餐总质量为300 g;
② 快餐的成分:蛋白质、碳水化合物、脂肪、矿物质;
③ 蛋白质和脂肪含量占50%;矿物质的含量是脂肪
含量的2倍;蛋白质和碳水化合物含量占85%。
根据上述数据回答下面的问题:
试分别求出营养快餐中蛋白质、碳水化合物、脂肪、矿物质的质量和所占百分比;
新知讲解
解: 设一份营养快餐中含蛋白质x (g)脂肪y (g) ,则矿物质为2y (g) ,碳水化合物为(300×85%-x) (g) .
由题意,得
①+②,得 3y=45,
解得 y=15 (g).
∴ x=150-y=135 (g),
2y=2×15=30(g),
300×85%-x=255-135=120(g)
新知讲解
中学生营养快餐成分统计表
将以上中学生营养快餐成分绘制成表格如下:
中学生营养快餐成分绘制成扇形统计图如右:
蛋白质 脂肪 矿物质 碳水化合物 合计
各种成分的质量(g) 135 15 30 120 300
各种成分所占百分比 45% 5% 10% 40% 100%
新知讲解
解信息量大,关系复杂的实际问题时,要仔细分析题意,找出等量关系,利用它们的数量关系适当地设元,然后列方程组解题.
课堂练习
1、设A、B两镇相距x千米,甲从A镇、乙从B镇同时出发,相向而行,甲、乙行驶的速度分别为u千米/小时、v千米/小时,并有:【版权所
①出发后30分钟相遇;
②甲到B镇后立即返回,追上乙时又经过了30分钟;
③当甲追上乙时他俩离A镇还有4千米.求x、u、v.
根据题意,由条件③,有四位同学各得到第3个方程如下,其中错误的一个是( )
A.x=u+4 B.x=v+4 C.2x﹣u=4 D.x﹣v=4
A
课堂练习
2、养牛场原有30头大牛和15头小牛,1天约用饲料675kg,一周后又购进12头大牛和5头小牛,这时1天约用饲料940kg。饲养员李大叔估计每头大牛每天约需饲料18~20kg,每头小牛每天约需饲料7~8kg。你能通过计算检验他的估计吗?
30×每头大牛量+15×每头小牛量=675
42×每头大牛量+20×每头小牛量=940
30x+15y=675
42x+20y=940
课堂练习
30x+15y=675 ①
42x+20y=940 ②
解:设每头大牛 x kg/天,每头小牛 y kg/天,则
解:由①,得
由②,得
2x+y=45 ③
2.1x+y=47 ④
④-③
0.1x=2
x=20
把x=20代入③,得
40+y=45
y=5
答:每头大牛20kg/天,每头小牛5kg/天,李大叔对大牛的估计正确,对小牛的估计不正确。
∴方程组的解为
课堂练习
3、张大叔承包的10亩地理所种植的甲、乙两种蔬菜共获利13800元,其中甲种蔬菜每亩获利1200元,乙种蔬菜每亩获利1500元.问甲、乙两种蔬菜各种植了多少亩?
分析:题目中的等量关系非常明显:甲乙两种蔬菜共种植10亩;甲乙两种蔬菜共获利13800元。由这两个等量关系列出方程组求解即可。
课堂总结
审→设→找→列→解→验→答
(1)审:审题,分析题中已知什么,求什么,明确各数量之间的关系.
(2)设:设未知数(一般求什么,就设什么为x,y).
(3)找:找出能够表示应用题全部意义的两个等量关系.
(4)列:根据这两个等量关系列出需要的代数式,进而列出两个方程,组成方程组.
(5)解:解所列方程组,得未知数的值.
(6)验:检验所求未知数的值是 否符合题意,是否符合实际.
(7)答:写出答案(包括单位名称).
列二元一次方程组解应用题的一般步骤:
板书设计
列二元一次方程组解应用题的一般步骤:
审→设→找→列→解→验→答
作业布置
教材49页习题第1、2、5、6题。
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
