2.5三元一次方程组及其解法 课件

2.5三元一次方程组及其解法
浙教版 七年级下
新知导入
1、什么叫二元一次方程组？
含有两个未知数，并且含有未知数的项的次数都是1，像这样的整式方程叫做二元一次方程。
2、怎样解二元一次方程组？
二元一次方程组
一元一次方程
代入
加减
新知讲解
一副扑克牌共54张，老师将一副扑克牌分给甲、乙、丙三名小朋友. 甲拿到的牌数是乙的2倍；若把丙拿到的牌分一半给乙，则乙的牌数就比甲多2张. 问老师分给甲、乙、丙各几张牌？
讨论：这个问题中要求的未知数有几个？你能列出关于这些未知数的几个方程？请试一试.
甲的牌数+乙的牌数+丙的牌数=54张
甲的牌数=2倍乙的牌数
等量关系式：
新知讲解
①甲的牌数+乙的牌数+丙的牌数=54张
②甲的牌数=2倍乙的牌数
设甲、乙、丙的牌数分别为x、y、z,根据题意得
①x+y+z=54
②x=2y
该方程组具有怎样的特征?
该方程组具有怎样的特征?
新知讲解
1．三元一次方程: 含有三个未知数, 并且所含未知数的项的次数都是1，这样的方程叫做三元一次方程．
必备条件：
(1)是整式方程；
(2)含三个未知数；
(3)所含未知数的项的次数都是1.
新知讲解
2．三元一次方程组：共含有三个未知数的三个一次方程所组成的一组方程，叫做三元一次方程组．
必备条件：
(1)是整式方程；
(2)共含三个未知数；
(3)三个都是一次方程；
(4)联立在一起．
新知讲解
新知讲解
解：①＋③ ，得5x＋5y=25 ④
①x2- ②，得5x-y=19. ⑤，则
把x＝4,y＝1代入① ,得z=-1
新知讲解
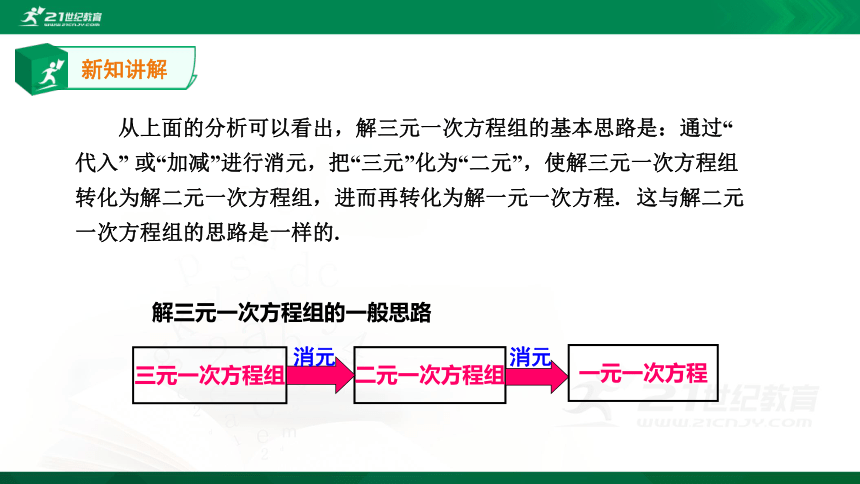
从上面的分析可以看出，解三元一次方程组的基本思路是：通过“代入” 或“加减”进行消元，把“三元”化为“二元”，使解三元一次方程组转化为解二元一次方程组，进而再转化为解一元一次方程. 这与解二元一次方程组的思路是一样的.
解三元一次方程组的一般思路
三元一次方程组
二元一次方程组
一元一次方程
消元
消元
新知讲解
解三元一次方程组的一般步骤：
(1)利用代入法或加减法消去三元一次方程组的一个未知数，得到关于另外两个未知数的二元一次方程组；
(2)解这个二元一次方程组，求出两个未知数的值；
(3)将求得的两个未知数的值代入原方程组中的一个系数比较简单的方程，得到一个一元一次方程；
(4)解这个一元一次方程，求出最后一个未知数的值；
(5)将求得的三个未知数的值用符号“{”合写在一起．
新课讲解
原方程组中有哪个方程还没有用到？
可不可以不用①？
注意：在消去一个未知数得出比原方程组少一个未知数的二元一次方程组的过程中，原方程组的每一个方程一般都至少要用到一次．
新课讲解
也可以这样解:
①+②+③,得2(x+y+z)=12 ④
即，x+y+z=6 ⑤
⑤－①,得z=3
⑤－②,得x=1
⑤－③，得y=2
课堂练习
1.解下列三元一次方程组：
课堂练习
2.若|a－b－1|＋(b－2a＋c)2 ＋|2c－b|＝0. 求a，b，c的值.
解:因为三个非负数的和等于零. 所以每个非负数都为零.可得方程组:
解得:
答: a，b，c的值分别为－3，－4，－2.
课堂练习
　　2．某学校中的篮球数比排球数的2倍少3，足球数与排球数的比是2∶3，三种球共41个，求三种球各有多少个．
　　解：设篮球有x个，排球有y个，足球有z个，
把①代入③，得3y＋z＝44，④
由④得z＝44－3y，⑤
根据题意得
课堂练习
把⑤代入②，得y＝12．
把y＝12分别代入①⑤，得x＝21，z＝8．
所以这个方程组的解为
答：篮球有21个，排球有12个，足球有8个．
课堂总结
回顾旧知
三元一次方程组
3.解三元一次方程组方法：消元法、加减法.基本思路是消元：三元
二元
一元．
1.三元一次方程:含有三个未知数, 并且所含未知数的项的次数都是1，这样的方程叫做三元一次方程．
2.三元一次方程组:由三个一次方程组成，并且含有三个未知数的方程， 叫做三元一次方程组．
板书设计
3.解三元一次方程组方法：消元法、加减法.基本思路是消元：三元
二元
一元．
1.三元一次方程:含有三个未知数, 并且所含未知数的项的次数都是1，这样的方程叫做三元一次方程．
2.三元一次方程组:由三个一次方程组成，并且含有三个未知数的方程， 叫做三元一次方程组．
作业布置
教材51页习题第1题。
教材52页习题第2、3、4、6题。
谢谢
21世纪教育网（www.21cnjy.com) 中小学教育资源网站
有大把高质量资料？一线教师？一线教研员？
欢迎加入21世纪教育网教师合作团队！！月薪过万不是梦！！
详情请看：
https://www.21cnjy.com/help/help_extract.php