浙教版数学七年级下册 1.3 平行线的判定 教案
文档属性
| 名称 | 浙教版数学七年级下册 1.3 平行线的判定 教案 | 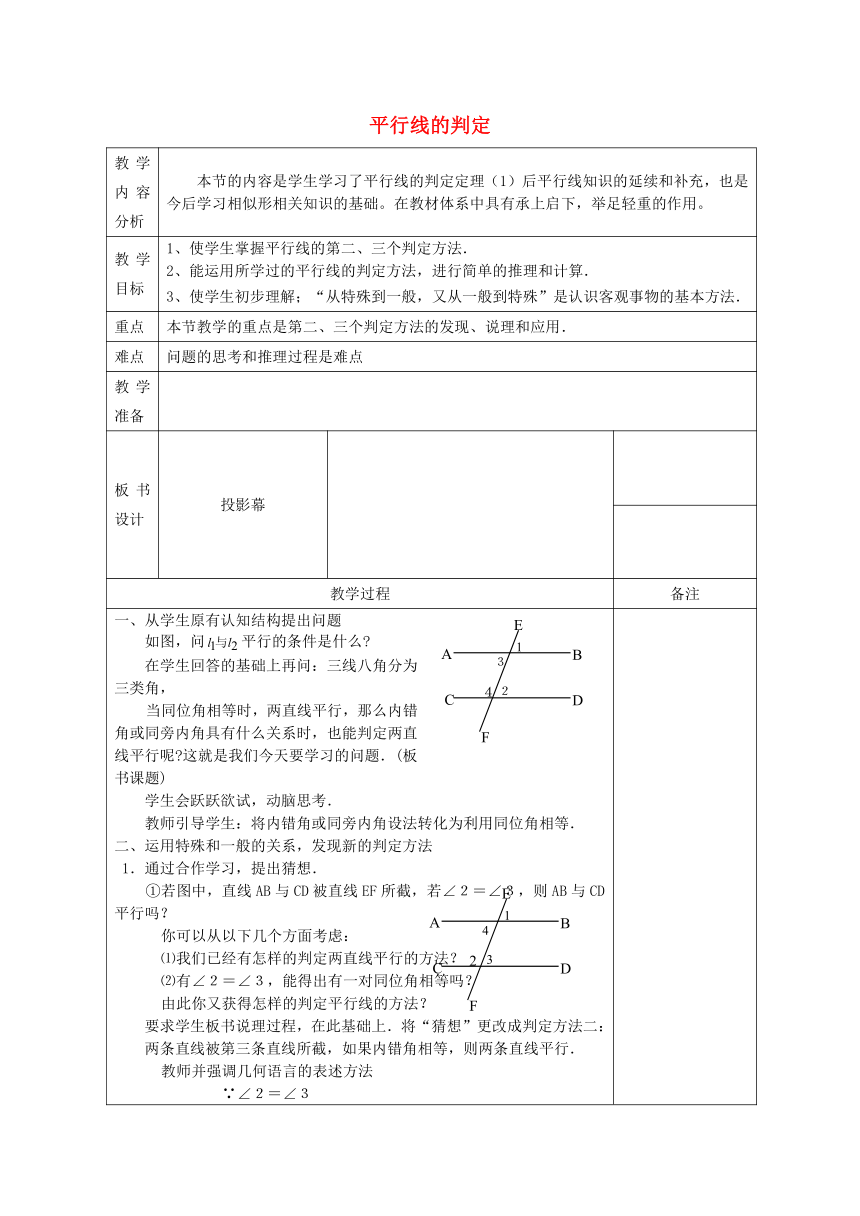 | |
| 格式 | zip | ||
| 文件大小 | 12.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-29 10:23:30 | ||
图片预览

文档简介
平行线的判定
教学内容分析
本节的内容是学生学习了平行线的判定定理(1)后平行线知识的延续和补充,也是今后学习相似形相关知识的基础。在教材体系中具有承上启下,举足轻重的作用。
教学目标
1、使学生掌握平行线的第二、三个判定方法.
2、能运用所学过的平行线的判定方法,进行简单的推理和计算.
3、使学生初步理解;“从特殊到一般,又从一般到特殊”是认识客观事物的基本方法.
重点
本节教学的重点是第二、三个判定方法的发现、说理和应用.
难点
问题的思考和推理过程是难点
教学准备
板书设计
投影幕
教学过程
备注
一、从学生原有认知结构提出问题
如图,问平行的条件是什么?
在学生回答的基础上再问:三线八角分为三类角,
当同位角相等时,两直线平行,那么内错角或同旁内角具有什么关系时,也能判定两直线平行呢?这就是我们今天要学习的问题.(板书课题)
学生会跃跃欲试,动脑思考.
教师引导学生:将内错角或同旁内角设法转化为利用同位角相等.
二、运用特殊和一般的关系,发现新的判定方法
1.通过合作学习,提出猜想.
①若图中,直线AB与CD被直线EF所截,若∠2=∠3,则AB与CD平行吗?
你可以从以下几个方面考虑:
⑴我们已经有怎样的判定两直线平行的方法?
⑵有∠2=∠3,能得出有一对同位角相等吗?
由此你又获得怎样的判定平行线的方法?
要求学生板书说理过程,在此基础上.将“猜想”更改成判定方法二:
两条直线被第三条直线所截,如果内错角相等,则两条直线平行.
教师并强调几何语言的表述方法
∵∠2=∠3
∴AB∥CD(内错角相等,两条直线平行)
然后,完成“做一做”
∠1=121°, ∠2=120°,∠3=120°。
说出其中的平行线,并说明理由 .
②若图中,直线AB与CD被直线EF所截,若∠2+∠4=180°,则AB与CD平行吗?
你可以由类似的方法得到正确的结论吗?
由此你又获得怎样的判定平行线的方法?
要求学生板书说理过程,在此基础上.将“猜想”更改成判定方法三:
两条直线被第三条直线所截,如果同旁内角互补,则两条直线平行.
教师并强调几何语言的表述方法
∵∠2+∠4=180°
∴AB∥CD(同旁内角互补,两条直线平行)
当学生都得到正确的结论后,引导学生猜想:同旁内角互补,两条直线平行.
在学生初步掌握这两个判定后,进行反速反应,学生的积极性又一次被调动起来,通过6个问题串,让学生亲自上台寻找平行线,并问学生找到平行线的依据。使学生初步熟练应用平行线的三个判定。接下来进入例题教学很自然,方法也会很多种。(注意:在第5张幻灯片下面有超级连接Authorwar,出现对话框,按确定便可进入Authorwar。学生演示完毕,按关闭键,回到原处,按鼠标,便可进入下一张幻灯片。)
快速反应
如图:
①若∠1=∠4,则 ∥
②若∠2=∠3,则 ∥
③若∠B=∠5,则 ∥
④若∠B+∠BCD=1800,则 ∥
⑤若∠5=∠D,则 ∥
⑦若∠B+∠BCD=1800,则 ∥
2.例题教学,体验新知
例2.如图,∠C+∠A=∠AEC。判断AB与CD是否平行,并说明理由。
分析:延长CE,交AB于点F,则直线CD,AB被直线CF所截。这样,
我们可以通过判断内错角∠C和∠AFC是否相等,来判定AB与CD是否平行。
板书解答过程。
提问:能否用不一样的方法来判定AB与CD是否平行?
提示:连结AC。
如图∠A+∠B+∠C+∠D=360°,且∠A=∠C,∠B=∠D,
那么AB∥CD ,AD∥BC.请说明理由。
先让学生思考,以小组为单位进行讨论,然后派出代表发言,学生基本上都能想到,用同旁内角互补,两条直线平行的判定,但书写难度较大,教师要加以引导说理过程
3、课堂小结
1.先由教师问学生:到目前为止学习了哪些判定两直线平行的方法?在选择方法时应注意什么问题?
2.在学生回答的基础上,教师总结指出:
(1)学习了3种判定方法.
(2)学习了由特殊到一般,又由一般到特殊的认识客观事物的基本方法.
(3)在平行线的判定问题中,要“有的放矢”,根据不同情况作出选择.
4、布置作业
作业本(1),选用课本题.
附: 多媒体课件
教学反思:
教学内容分析
本节的内容是学生学习了平行线的判定定理(1)后平行线知识的延续和补充,也是今后学习相似形相关知识的基础。在教材体系中具有承上启下,举足轻重的作用。
教学目标
1、使学生掌握平行线的第二、三个判定方法.
2、能运用所学过的平行线的判定方法,进行简单的推理和计算.
3、使学生初步理解;“从特殊到一般,又从一般到特殊”是认识客观事物的基本方法.
重点
本节教学的重点是第二、三个判定方法的发现、说理和应用.
难点
问题的思考和推理过程是难点
教学准备
板书设计
投影幕
教学过程
备注
一、从学生原有认知结构提出问题
如图,问平行的条件是什么?
在学生回答的基础上再问:三线八角分为三类角,
当同位角相等时,两直线平行,那么内错角或同旁内角具有什么关系时,也能判定两直线平行呢?这就是我们今天要学习的问题.(板书课题)
学生会跃跃欲试,动脑思考.
教师引导学生:将内错角或同旁内角设法转化为利用同位角相等.
二、运用特殊和一般的关系,发现新的判定方法
1.通过合作学习,提出猜想.
①若图中,直线AB与CD被直线EF所截,若∠2=∠3,则AB与CD平行吗?
你可以从以下几个方面考虑:
⑴我们已经有怎样的判定两直线平行的方法?
⑵有∠2=∠3,能得出有一对同位角相等吗?
由此你又获得怎样的判定平行线的方法?
要求学生板书说理过程,在此基础上.将“猜想”更改成判定方法二:
两条直线被第三条直线所截,如果内错角相等,则两条直线平行.
教师并强调几何语言的表述方法
∵∠2=∠3
∴AB∥CD(内错角相等,两条直线平行)
然后,完成“做一做”
∠1=121°, ∠2=120°,∠3=120°。
说出其中的平行线,并说明理由 .
②若图中,直线AB与CD被直线EF所截,若∠2+∠4=180°,则AB与CD平行吗?
你可以由类似的方法得到正确的结论吗?
由此你又获得怎样的判定平行线的方法?
要求学生板书说理过程,在此基础上.将“猜想”更改成判定方法三:
两条直线被第三条直线所截,如果同旁内角互补,则两条直线平行.
教师并强调几何语言的表述方法
∵∠2+∠4=180°
∴AB∥CD(同旁内角互补,两条直线平行)
当学生都得到正确的结论后,引导学生猜想:同旁内角互补,两条直线平行.
在学生初步掌握这两个判定后,进行反速反应,学生的积极性又一次被调动起来,通过6个问题串,让学生亲自上台寻找平行线,并问学生找到平行线的依据。使学生初步熟练应用平行线的三个判定。接下来进入例题教学很自然,方法也会很多种。(注意:在第5张幻灯片下面有超级连接Authorwar,出现对话框,按确定便可进入Authorwar。学生演示完毕,按关闭键,回到原处,按鼠标,便可进入下一张幻灯片。)
快速反应
如图:
①若∠1=∠4,则 ∥
②若∠2=∠3,则 ∥
③若∠B=∠5,则 ∥
④若∠B+∠BCD=1800,则 ∥
⑤若∠5=∠D,则 ∥
⑦若∠B+∠BCD=1800,则 ∥
2.例题教学,体验新知
例2.如图,∠C+∠A=∠AEC。判断AB与CD是否平行,并说明理由。
分析:延长CE,交AB于点F,则直线CD,AB被直线CF所截。这样,
我们可以通过判断内错角∠C和∠AFC是否相等,来判定AB与CD是否平行。
板书解答过程。
提问:能否用不一样的方法来判定AB与CD是否平行?
提示:连结AC。
如图∠A+∠B+∠C+∠D=360°,且∠A=∠C,∠B=∠D,
那么AB∥CD ,AD∥BC.请说明理由。
先让学生思考,以小组为单位进行讨论,然后派出代表发言,学生基本上都能想到,用同旁内角互补,两条直线平行的判定,但书写难度较大,教师要加以引导说理过程
3、课堂小结
1.先由教师问学生:到目前为止学习了哪些判定两直线平行的方法?在选择方法时应注意什么问题?
2.在学生回答的基础上,教师总结指出:
(1)学习了3种判定方法.
(2)学习了由特殊到一般,又由一般到特殊的认识客观事物的基本方法.
(3)在平行线的判定问题中,要“有的放矢”,根据不同情况作出选择.
4、布置作业
作业本(1),选用课本题.
附: 多媒体课件
教学反思:
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
