浙教版数学七年级下册 1.2《同位角、内错角、同旁内角》 课件(共27张PPT)
文档属性
| 名称 | 浙教版数学七年级下册 1.2《同位角、内错角、同旁内角》 课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-01 17:22:05 | ||
图片预览


文档简介
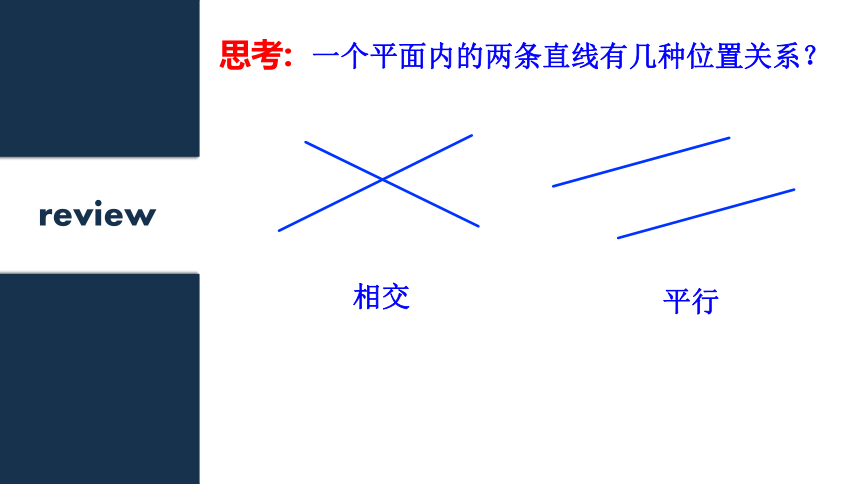
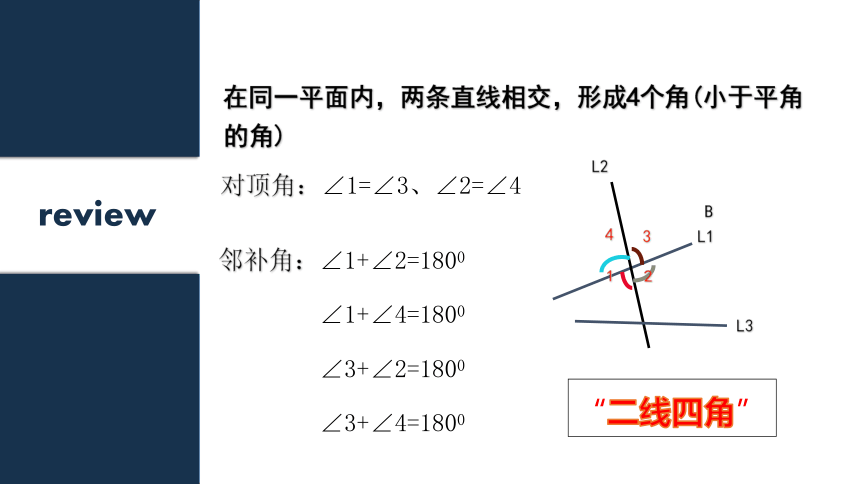
课件27张PPT。同位角,内错角,同旁内角1.2review相交平行思考: 一个平面内的两条直线有几种位置关系?在同一平面内,两条直线相交,形成4个角(小于平角的角)L2对顶角:∠1=∠3、∠2=∠4邻补角:∠1+∠2=1800
∠1+∠4=1800
∠3+∠2=1800
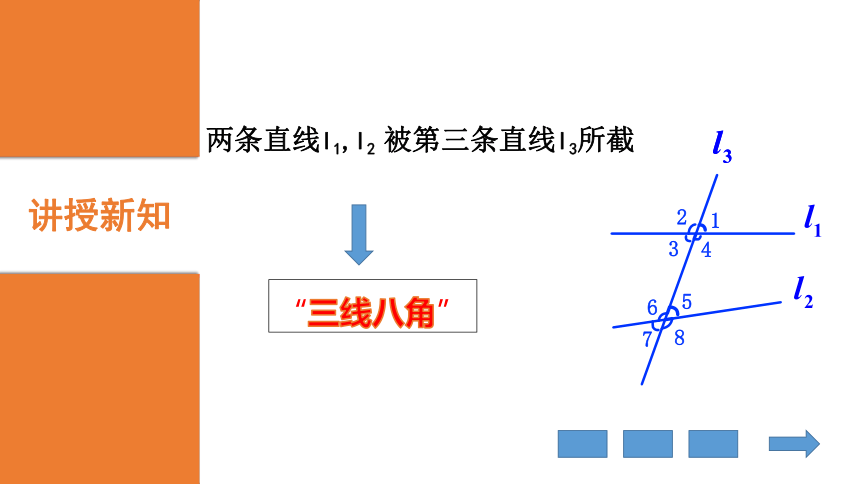
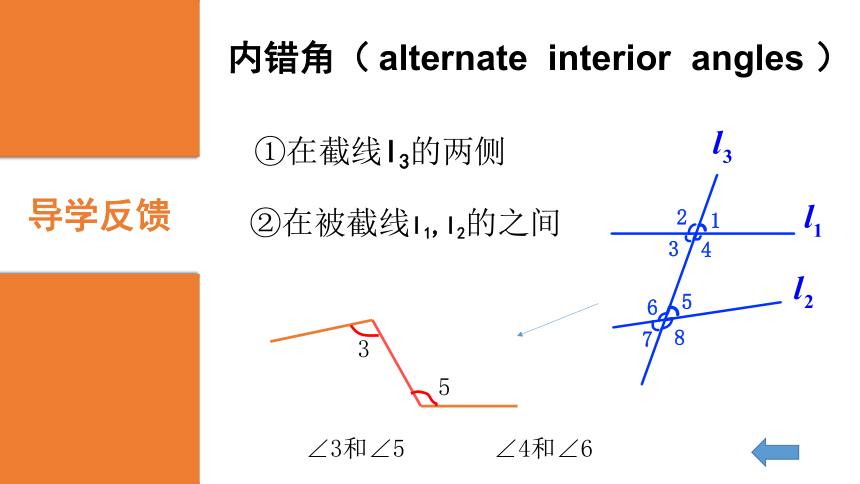
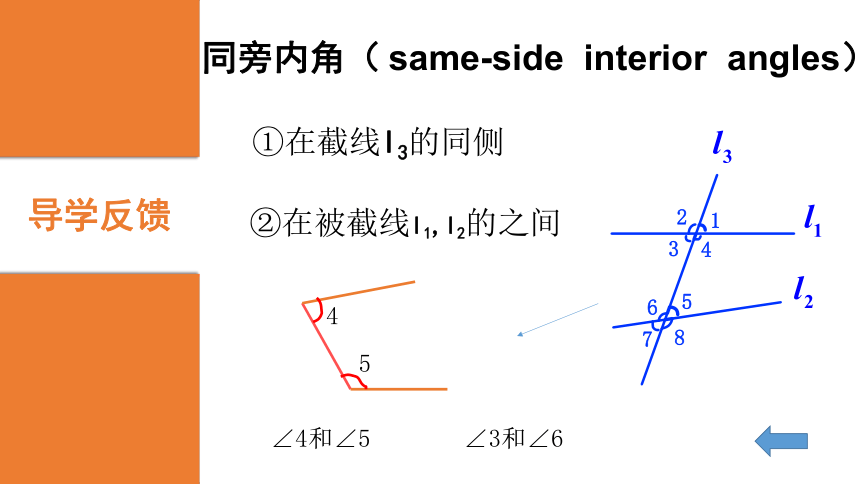
∠3+∠4=1800“二线四角”reviewL3“三线八角”讲授新知两条直线l1,l2 被第三条直线l3所截导学反馈同位角(corresponding angles)①在截线l3的同侧②在被截线l1,l2的同侧∠1和∠5∠2和∠6∠3和∠7∠4和∠8导学反馈内错角( alternate interior angles )①在截线l3的两侧②在被截线l1,l2的之间∠3和∠5∠4和∠6导学反馈同旁内角( same-side interior angles)②在被截线l1,l2的之间①在截线l3的同侧
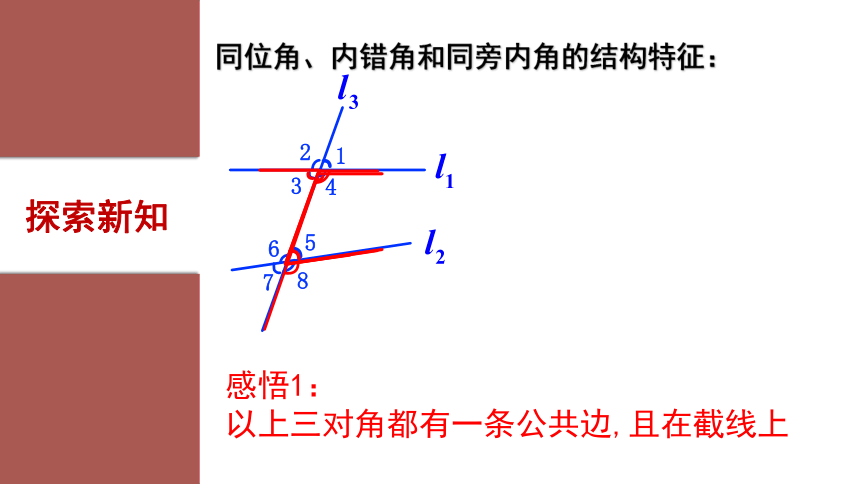
∠4和∠5∠3和∠6同位角、内错角和同旁内角的结构特征:感悟1:
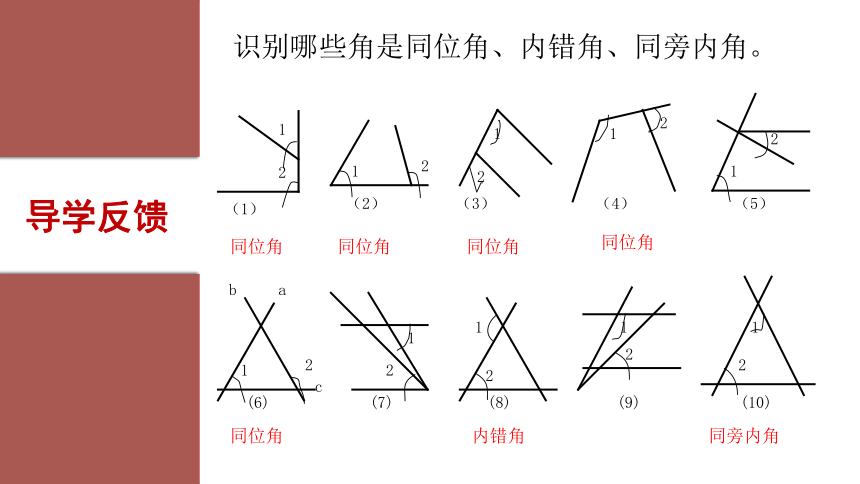
以上三对角都有一条公共边,且在截线上探索新知识别哪些角是同位角、内错角、同旁内角。12(1)同位角12(2)12(3)12(4)12(5)abc12(6)12(7)12(8)1212(9)(10)同位角同位角同位角同位角内错角同旁内角导学反馈中级挑战初级挑战 例1:已知直线l1,l2,l3,l4(如图).
(1)当直线_____和_____被直线_____
所截时,∠1与∠3是同位角;
当直线_____和_____被直线_____
所截时,∠1与∠4是内错角;
当直线_____和_____被直线_____
所截时,∠4与∠5是同旁内角.
(2)在所标示的角中,请找出图中的一对同位角、内错角和同旁内角,并分别说明是哪两条直线被哪条直线所截而成的.
l3l4l1l27l1l2l3l3l4l1l1l2l4感悟2:
解题前要先确定“哪两条直线被哪条直线所截”,初级挑战 变式:已知直线l1,l2,l3,l4(如图). 你能数出这个图中的同位角,内错角,同旁内角的对数吗?
初级挑战同位角:16对内错角:8对同旁内角:8对感悟3:
求一个图形中的三类角的对数时要利用“三线八角”的基本图形
请找出图中所有的同位角、内错角和同旁内角.同位角:内错角:同旁内角:∠A和∠EDC∠C和∠ABF∠C和∠EDC∠A和∠ABF∠A和∠ABC∠A和∠ADC∠C和∠ABC∠C和∠ADC合作交流高级挑战例2:如图,
如果∠1=∠2,
那么∠1=∠4,∠1与∠3互补.
请说明理由.高级挑战如果内错角相等,
那么同位角相等,同旁内角互补.内错角相等同位角相等同旁内角互补变式1:如图,
如果∠1=∠4,
那么∠1=∠2,∠1与∠3互补.
请说明理由.高级挑战如果同位角相等,
那么内错角相等,同旁内角互补.同位角相等内错角相等同旁内角互补变式2:如图,
如果∠1与∠3互补,
那么∠1=∠2,∠1与∠4.
请说明理由.高级挑战如果同旁内角互补,
那么内错角相等,同位角相等.同旁内角互补内错角相等同位角相等高级挑战感悟4:
同位角相等,内错角相等,同旁内角互补.
这3者中若有一个成立,则另两个也成立。课堂小结畅所欲言
请谈一谈你这节课的收获……GAME如图,∠1与∠2是同位角的是如图:若ED,BF被AB所截,则∠1与_____是同位角.∠2如图:若ED,BC被AF所截,则∠3与_____是内错角.∠4如图:∠1与∠3是AB和AF被_____所截构成的_______角.DE内错如图:∠2与∠4是_____和_____被BC所截构成的______角.ABAF同位
∠1+∠4=1800
∠3+∠2=1800
∠3+∠4=1800“二线四角”reviewL3“三线八角”讲授新知两条直线l1,l2 被第三条直线l3所截导学反馈同位角(corresponding angles)①在截线l3的同侧②在被截线l1,l2的同侧∠1和∠5∠2和∠6∠3和∠7∠4和∠8导学反馈内错角( alternate interior angles )①在截线l3的两侧②在被截线l1,l2的之间∠3和∠5∠4和∠6导学反馈同旁内角( same-side interior angles)②在被截线l1,l2的之间①在截线l3的同侧
∠4和∠5∠3和∠6同位角、内错角和同旁内角的结构特征:感悟1:
以上三对角都有一条公共边,且在截线上探索新知识别哪些角是同位角、内错角、同旁内角。12(1)同位角12(2)12(3)12(4)12(5)abc12(6)12(7)12(8)1212(9)(10)同位角同位角同位角同位角内错角同旁内角导学反馈中级挑战初级挑战 例1:已知直线l1,l2,l3,l4(如图).
(1)当直线_____和_____被直线_____
所截时,∠1与∠3是同位角;
当直线_____和_____被直线_____
所截时,∠1与∠4是内错角;
当直线_____和_____被直线_____
所截时,∠4与∠5是同旁内角.
(2)在所标示的角中,请找出图中的一对同位角、内错角和同旁内角,并分别说明是哪两条直线被哪条直线所截而成的.
l3l4l1l27l1l2l3l3l4l1l1l2l4感悟2:
解题前要先确定“哪两条直线被哪条直线所截”,初级挑战 变式:已知直线l1,l2,l3,l4(如图). 你能数出这个图中的同位角,内错角,同旁内角的对数吗?
初级挑战同位角:16对内错角:8对同旁内角:8对感悟3:
求一个图形中的三类角的对数时要利用“三线八角”的基本图形
请找出图中所有的同位角、内错角和同旁内角.同位角:内错角:同旁内角:∠A和∠EDC∠C和∠ABF∠C和∠EDC∠A和∠ABF∠A和∠ABC∠A和∠ADC∠C和∠ABC∠C和∠ADC合作交流高级挑战例2:如图,
如果∠1=∠2,
那么∠1=∠4,∠1与∠3互补.
请说明理由.高级挑战如果内错角相等,
那么同位角相等,同旁内角互补.内错角相等同位角相等同旁内角互补变式1:如图,
如果∠1=∠4,
那么∠1=∠2,∠1与∠3互补.
请说明理由.高级挑战如果同位角相等,
那么内错角相等,同旁内角互补.同位角相等内错角相等同旁内角互补变式2:如图,
如果∠1与∠3互补,
那么∠1=∠2,∠1与∠4.
请说明理由.高级挑战如果同旁内角互补,
那么内错角相等,同位角相等.同旁内角互补内错角相等同位角相等高级挑战感悟4:
同位角相等,内错角相等,同旁内角互补.
这3者中若有一个成立,则另两个也成立。课堂小结畅所欲言
请谈一谈你这节课的收获……GAME如图,∠1与∠2是同位角的是如图:若ED,BF被AB所截,则∠1与_____是同位角.∠2如图:若ED,BC被AF所截,则∠3与_____是内错角.∠4如图:∠1与∠3是AB和AF被_____所截构成的_______角.DE内错如图:∠2与∠4是_____和_____被BC所截构成的______角.ABAF同位
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
