浙教版七年级下册3.6同底数幂的除法课件(共19张PPT)
文档属性
| 名称 | 浙教版七年级下册3.6同底数幂的除法课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 204.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-13 07:23:30 | ||
图片预览




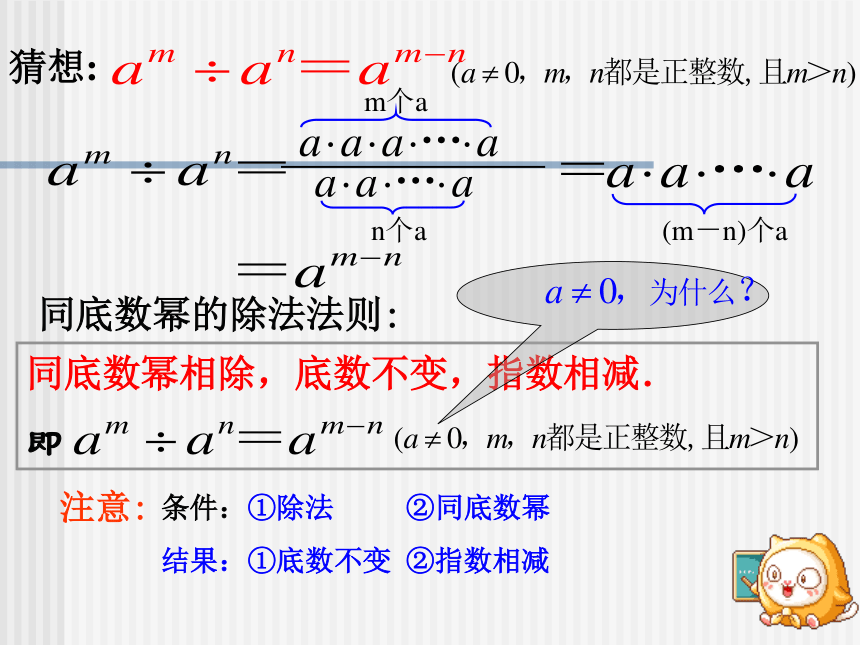


文档简介
课件19张PPT。3.6 同底数幂的除法(1)温故知新同底数幂的乘法: am·an=am+n (m、n都是正整数)
幂的乘方: (am)n=amn (m、n都是正整数)
积的乘方: (ab)n= anbn (n为正整数)
计算:
1. (-a)3.(-a)2=
2. (ab)5=
3. (ym)3=-a5a5b5y3m=?创设情景,引入新知合作探究=2 2 = 2 5-3 1思考:观察上面各题左右两边,底数、指数有什么关系?(m-n)个am个an个a同底数幂相除,底数不变,指数相减.
即同底数幂的除法法则:条件:①除法 ②同底数幂
结果:①底数不变 ②指数相减注意:(1) a9÷a3(2) 212÷27例1 计算:=a9-3 = a6=212-7=25=32(3) (- x)4÷(- x )=(- x)4-1=(- x)3= - x3(4) (- 3)11÷ (- 3)8 =(- 3)11-8=(- 3)3=- 27运算结果的底数一般应化为正数;
不能疏忽指数为1的情况;(8) (ab2)5÷(ab2)2=(ab2)5-2=(ab2)3
=a3b6(6) (a+b)6÷(a+b)4=(a+b)6-4=(a+b)2=a2+2ab+b2(7) (y8)2÷ y8= (y8)2-1 = y8= y16 ÷ y8 = y8公式中的字母
可以是一个数,
也可以是单项式,
多项式(5) b2m+2÷ b2=b2m+2-2=b2m练一练:1. 下列计算对吗? 为什么? 错的请改正.错错错错课本p83作业题12、(口答)计算:
(1) s7÷s3= (2) x10÷x8=
(3)(-t)11÷ (-t)2= (4) (ab)5÷(ab)=
(5) (-3)6÷ (-3)2= (6) a100÷a100=
S4181a4b4-t9x2课本p83课内练习13.填空:课本p83课内练习2解:(1)原式=a5-4+2=a3(2)原式=-x7÷x2=-x7-2=-x5(3)原式=(ab)5-2=(ab)3=a3b3(4)原式=(a+b)6-4=(a+b)2
=a2+2ab+b2若底数不同,先化为同底数,后运用法则.
乘除混合运算的顺序与有理数混合运算顺序
相同(即“从左到右”).
运算结果能化简的要进行化简.例2 计算:课本p83课内练习3注意:在应用同底数幂相除的法则时,底数必须是相同的 (-x)4÷x (2)(ab)5÷(a2b2)
(3) (-b)4÷(-b2) (4) (a-b)3÷(b-a)2
(5)323÷47例3 计算:应用生活: 金星是太阳系九大行星中距离地球最近的行星,也是人在地球上看到的天空中最亮的一颗星。金星离地球的距离为4.2×107千米,从金星射出的光到达地球需要多少时间?(光的速度为3.0×105千米/秒 )谈谈你的收获与体会同底数幂相除的法则是:同底数幂相除,底数不变,指数相减.
即 1.一个式子中有多种运算时,要明确运算的先后顺序. 2.底数为分数、负数、多项式时,运算过程要加括号.理一理 再质疑不要遗漏指数为1的情况。公式中的字母可以是一个数,也可以是单项式或多项式。在应用同底数幂相除的法则时,底数必须是相同的。在进行混合运算时要注意运算顺序。 am ÷ an = am-n (a≠0,m、n为正整数,m>n)注意点特别注意运算中符号的变化。1. 若n为正整数, 则 n =____96提高创新题3、计算下列各题:
(1) x4n+1÷x 2n-1·x2n+1= ?
(2)已知ax=2 ,ay=3 则ax-y= ?
(3)已知ax=2,ay=3 则 a2x-y= ?
(4)已知am=4 ,an=5 求a3m-2n的值。
(5) 已知2x-5y-4=0,求4x÷32y的值。
(6)若10a=20 ,10b=1/5,试求9a÷32b的值。提高创新题
幂的乘方: (am)n=amn (m、n都是正整数)
积的乘方: (ab)n= anbn (n为正整数)
计算:
1. (-a)3.(-a)2=
2. (ab)5=
3. (ym)3=-a5a5b5y3m=?创设情景,引入新知合作探究=2 2 = 2 5-3 1思考:观察上面各题左右两边,底数、指数有什么关系?(m-n)个am个an个a同底数幂相除,底数不变,指数相减.
即同底数幂的除法法则:条件:①除法 ②同底数幂
结果:①底数不变 ②指数相减注意:(1) a9÷a3(2) 212÷27例1 计算:=a9-3 = a6=212-7=25=32(3) (- x)4÷(- x )=(- x)4-1=(- x)3= - x3(4) (- 3)11÷ (- 3)8 =(- 3)11-8=(- 3)3=- 27运算结果的底数一般应化为正数;
不能疏忽指数为1的情况;(8) (ab2)5÷(ab2)2=(ab2)5-2=(ab2)3
=a3b6(6) (a+b)6÷(a+b)4=(a+b)6-4=(a+b)2=a2+2ab+b2(7) (y8)2÷ y8= (y8)2-1 = y8= y16 ÷ y8 = y8公式中的字母
可以是一个数,
也可以是单项式,
多项式(5) b2m+2÷ b2=b2m+2-2=b2m练一练:1. 下列计算对吗? 为什么? 错的请改正.错错错错课本p83作业题12、(口答)计算:
(1) s7÷s3= (2) x10÷x8=
(3)(-t)11÷ (-t)2= (4) (ab)5÷(ab)=
(5) (-3)6÷ (-3)2= (6) a100÷a100=
S4181a4b4-t9x2课本p83课内练习13.填空:课本p83课内练习2解:(1)原式=a5-4+2=a3(2)原式=-x7÷x2=-x7-2=-x5(3)原式=(ab)5-2=(ab)3=a3b3(4)原式=(a+b)6-4=(a+b)2
=a2+2ab+b2若底数不同,先化为同底数,后运用法则.
乘除混合运算的顺序与有理数混合运算顺序
相同(即“从左到右”).
运算结果能化简的要进行化简.例2 计算:课本p83课内练习3注意:在应用同底数幂相除的法则时,底数必须是相同的 (-x)4÷x (2)(ab)5÷(a2b2)
(3) (-b)4÷(-b2) (4) (a-b)3÷(b-a)2
(5)323÷47例3 计算:应用生活: 金星是太阳系九大行星中距离地球最近的行星,也是人在地球上看到的天空中最亮的一颗星。金星离地球的距离为4.2×107千米,从金星射出的光到达地球需要多少时间?(光的速度为3.0×105千米/秒 )谈谈你的收获与体会同底数幂相除的法则是:同底数幂相除,底数不变,指数相减.
即 1.一个式子中有多种运算时,要明确运算的先后顺序. 2.底数为分数、负数、多项式时,运算过程要加括号.理一理 再质疑不要遗漏指数为1的情况。公式中的字母可以是一个数,也可以是单项式或多项式。在应用同底数幂相除的法则时,底数必须是相同的。在进行混合运算时要注意运算顺序。 am ÷ an = am-n (a≠0,m、n为正整数,m>n)注意点特别注意运算中符号的变化。1. 若n为正整数, 则 n =____96提高创新题3、计算下列各题:
(1) x4n+1÷x 2n-1·x2n+1= ?
(2)已知ax=2 ,ay=3 则ax-y= ?
(3)已知ax=2,ay=3 则 a2x-y= ?
(4)已知am=4 ,an=5 求a3m-2n的值。
(5) 已知2x-5y-4=0,求4x÷32y的值。
(6)若10a=20 ,10b=1/5,试求9a÷32b的值。提高创新题
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
