浙教版数学七年级下册2.3解二元一次方程组课件 共20张PPT
文档属性
| 名称 | 浙教版数学七年级下册2.3解二元一次方程组课件 共20张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-22 00:00:00 | ||
图片预览






文档简介
课件20张PPT。2.3.1 解二元一次方程组第二章 二元一次方程组Xing热身 已知方程3x=1-4y,按要求改写:
(1)用含x的代数式表示y;
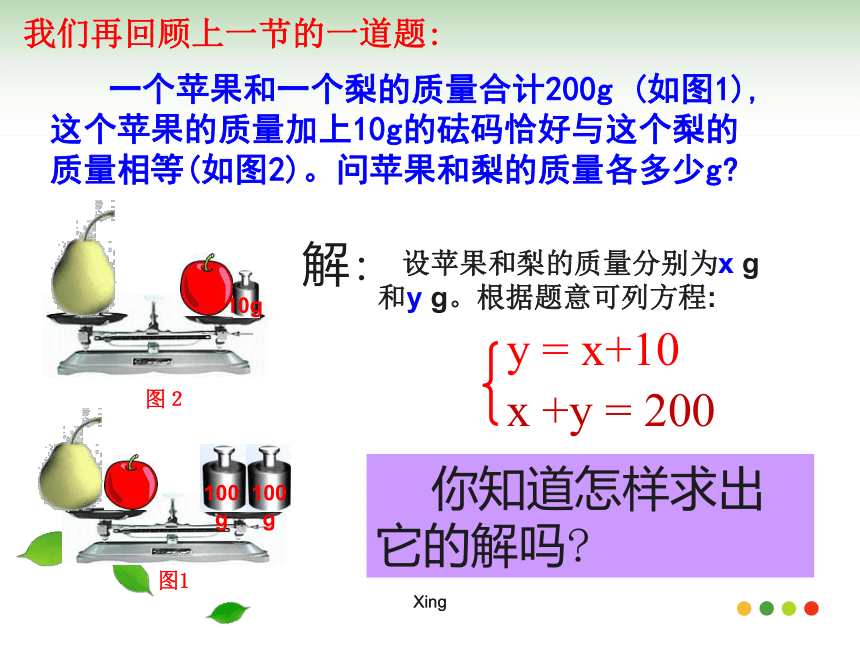
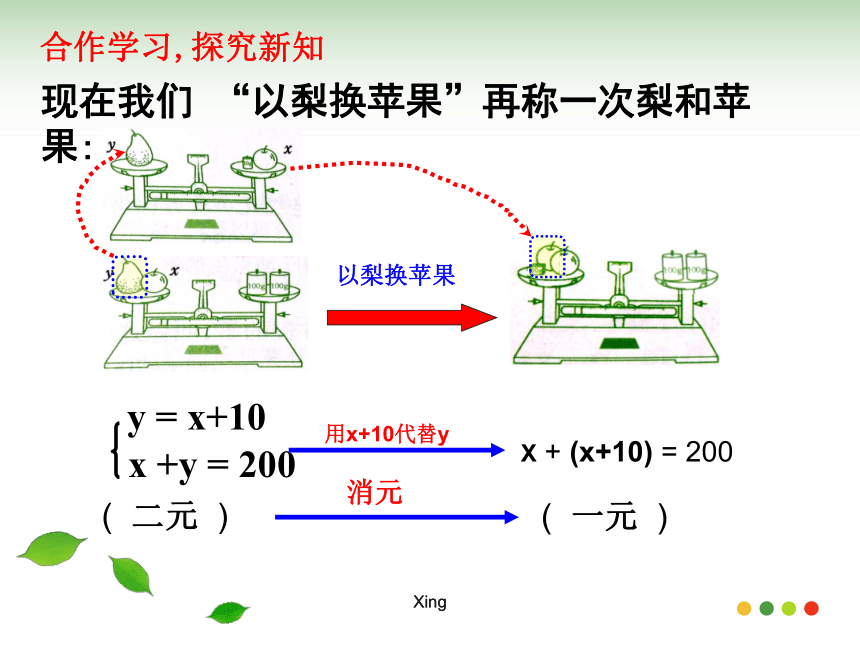
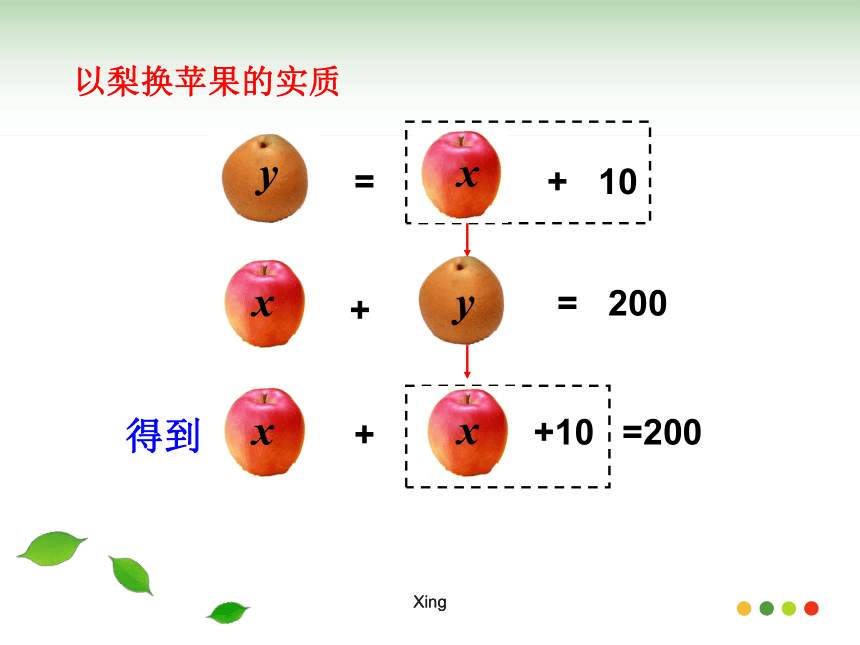
(2)用含y的代数式表示x.Xing 一个苹果和一个梨的质量合计200g (如图1),这个苹果的质量加上10g的砝码恰好与这个梨的质量相等(如图2)。问苹果和梨的质量各多少g? x +y = 200y = x+10 你知道怎样求出它的解吗?我们再回顾上一节的一道题:解: 设苹果和梨的质量分别为x g 和y g。根据题意可列方程:Xingx +y = 200y = x+10现在我们 “以梨换苹果”再称一次梨和苹果:用x+10代替yX + (x+10) = 200( 二元 )( 一元 ) 消元 以梨换苹果合作学习,探究新知Xing以梨换苹果的实质+=+ 10= 200+10+=200xyxxxy得到Xing 即:苹果和梨的质量分别为95g和105g. x+( x+10)=2002x+10=200x = 95 = 95 + 10
= 105 ②怎样代入? 这1个苹果的质量x加上10g的砝码恰好与这1个梨的质量y相等,即x+10与y的大小相等(等量代换).解:①为什么可以代入?∴y = x+10Xing 解二元一次方程组的基本思路是“消元”:二元化一元。“消元” 的方法是“代入” ,这种解方程组的方法称为代入消元法,简称代入法. 上面解方程组的基本思路是什么? Xing例1:解方程组① ② 2y-3(y-1)=12y-3y+3=1∴y=22y-3x=1
x=y-1把求出的解代入原方程组,可以知道你解得对不对。 Xing我国古代数学名著《孙子算经》上有这样一道题:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几头? 解决鸡兔同笼问题解: 设有笼中有鸡x只,有兔y只。则可列出方程组:x + y = 352x + 4y = 94下面请同学们自己解这个方程组!Xing
练一练:提示:②用含哪个未知数的代数式表示另一个未知数?有一个未知数的系数是1. 系数不为1的未知数的代数式表示另一个系数为1的未知数.①你认为具有什么特征的方程用代入法比较方便?1.解下列方程组Xing解: 2x = 8+7y即 ③ 把③代入②,得 例2:解方程组∴ 方程组的解是 由①,得 可由方程①用一个未知数的代数式表示另一未知数,再代入另一方程!Xing代入消元法解二元一次方程组的一般步骤: ②用这个代数式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值; ③把这个未知数的值代入代数式(回代) ,求得另一个未知数的值; ①将方程组中一个方程变形,使得一个未知数能含有另一个未知数的代数式表示;④写出方程组的解。即: 变形代替回代写出解归纳Xing提高巩固1.解下列二元一次方程组你认为怎样代入更简便? 请用你最简便的方法解出它的解.你的思路能解另一题吗?Xingx+1=2(y-1)
3(x+1)=5(y-1)+4①
②⑴1.解下列二元一次方程组可将(x+1)、(y-1)看作一个整体求解。 解: 把①代入② 3×2(y-1)= 5(y-1) + 4 6(y-1) =5(y-1)+4 (y-1) = 4 ③ ∴ y = 5 把③代入①x +1 = 2×4∴ x = 7 x +1=8 得 得:Xing①
②3x+2y=13
x - 2y = 5⑵解下列二元一次方程组可将2y看作一个数来求解。解: 由②得:把③代入① 3x + (x – 5) = 13 4x = 18 ∴ x = 4.5把x = 4.5代入③2y = 4.5 – 5 = – 0.5 ∴ y = -0.25 2y = x – 5 ③ 得: 得: Xing1.消元实质2.代入法的一般步骤3.学会检验,能灵活运用适当方法解二元一次方程组。即:变形代替回代写解用一个未知数的代数式表示另一个未知数
代入另一方程后,消去一个元
把求出的未知数代入代数式
写出方程组的解
小结Xing1.用代入法解方程组:强化练习:Xing-3强化练习:3、已知:x=t-2,y=2t+1,用含x的代数式表示y4、已知 和
是ax+by=1的两个解,求a+b的值Xing4.已知 和
是ax+by=1的两个解,求a+b的值由 得:b=1-2a①③得:a=1得:b=-1a+b=0Thank You!
(1)用含x的代数式表示y;
(2)用含y的代数式表示x.Xing 一个苹果和一个梨的质量合计200g (如图1),这个苹果的质量加上10g的砝码恰好与这个梨的质量相等(如图2)。问苹果和梨的质量各多少g? x +y = 200y = x+10 你知道怎样求出它的解吗?我们再回顾上一节的一道题:解: 设苹果和梨的质量分别为x g 和y g。根据题意可列方程:Xingx +y = 200y = x+10现在我们 “以梨换苹果”再称一次梨和苹果:用x+10代替yX + (x+10) = 200( 二元 )( 一元 ) 消元 以梨换苹果合作学习,探究新知Xing以梨换苹果的实质+=+ 10= 200+10+=200xyxxxy得到Xing 即:苹果和梨的质量分别为95g和105g. x+( x+10)=2002x+10=200x = 95 = 95 + 10
= 105 ②怎样代入? 这1个苹果的质量x加上10g的砝码恰好与这1个梨的质量y相等,即x+10与y的大小相等(等量代换).解:①为什么可以代入?∴y = x+10Xing 解二元一次方程组的基本思路是“消元”:二元化一元。“消元” 的方法是“代入” ,这种解方程组的方法称为代入消元法,简称代入法. 上面解方程组的基本思路是什么? Xing例1:解方程组① ② 2y-3(y-1)=12y-3y+3=1∴y=22y-3x=1
x=y-1把求出的解代入原方程组,可以知道你解得对不对。 Xing我国古代数学名著《孙子算经》上有这样一道题:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几头? 解决鸡兔同笼问题解: 设有笼中有鸡x只,有兔y只。则可列出方程组:x + y = 352x + 4y = 94下面请同学们自己解这个方程组!Xing
练一练:提示:②用含哪个未知数的代数式表示另一个未知数?有一个未知数的系数是1. 系数不为1的未知数的代数式表示另一个系数为1的未知数.①你认为具有什么特征的方程用代入法比较方便?1.解下列方程组Xing解: 2x = 8+7y即 ③ 把③代入②,得 例2:解方程组∴ 方程组的解是 由①,得 可由方程①用一个未知数的代数式表示另一未知数,再代入另一方程!Xing代入消元法解二元一次方程组的一般步骤: ②用这个代数式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值; ③把这个未知数的值代入代数式(回代) ,求得另一个未知数的值; ①将方程组中一个方程变形,使得一个未知数能含有另一个未知数的代数式表示;④写出方程组的解。即: 变形代替回代写出解归纳Xing提高巩固1.解下列二元一次方程组你认为怎样代入更简便? 请用你最简便的方法解出它的解.你的思路能解另一题吗?Xingx+1=2(y-1)
3(x+1)=5(y-1)+4①
②⑴1.解下列二元一次方程组可将(x+1)、(y-1)看作一个整体求解。 解: 把①代入② 3×2(y-1)= 5(y-1) + 4 6(y-1) =5(y-1)+4 (y-1) = 4 ③ ∴ y = 5 把③代入①x +1 = 2×4∴ x = 7 x +1=8 得 得:Xing①
②3x+2y=13
x - 2y = 5⑵解下列二元一次方程组可将2y看作一个数来求解。解: 由②得:把③代入① 3x + (x – 5) = 13 4x = 18 ∴ x = 4.5把x = 4.5代入③2y = 4.5 – 5 = – 0.5 ∴ y = -0.25 2y = x – 5 ③ 得: 得: Xing1.消元实质2.代入法的一般步骤3.学会检验,能灵活运用适当方法解二元一次方程组。即:变形代替回代写解用一个未知数的代数式表示另一个未知数
代入另一方程后,消去一个元
把求出的未知数代入代数式
写出方程组的解
小结Xing1.用代入法解方程组:强化练习:Xing-3强化练习:3、已知:x=t-2,y=2t+1,用含x的代数式表示y4、已知 和
是ax+by=1的两个解,求a+b的值Xing4.已知 和
是ax+by=1的两个解,求a+b的值由 得:b=1-2a①③得:a=1得:b=-1a+b=0Thank You!
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
