浙教版七年级数学下册1.2 同位角、内错角、同旁内角同步练习含答案
文档属性
| 名称 | 浙教版七年级数学下册1.2 同位角、内错角、同旁内角同步练习含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 814.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-20 08:59:41 | ||
图片预览


文档简介
1.2 同位角、内错角、同旁内角
一、选择题(共8小题)
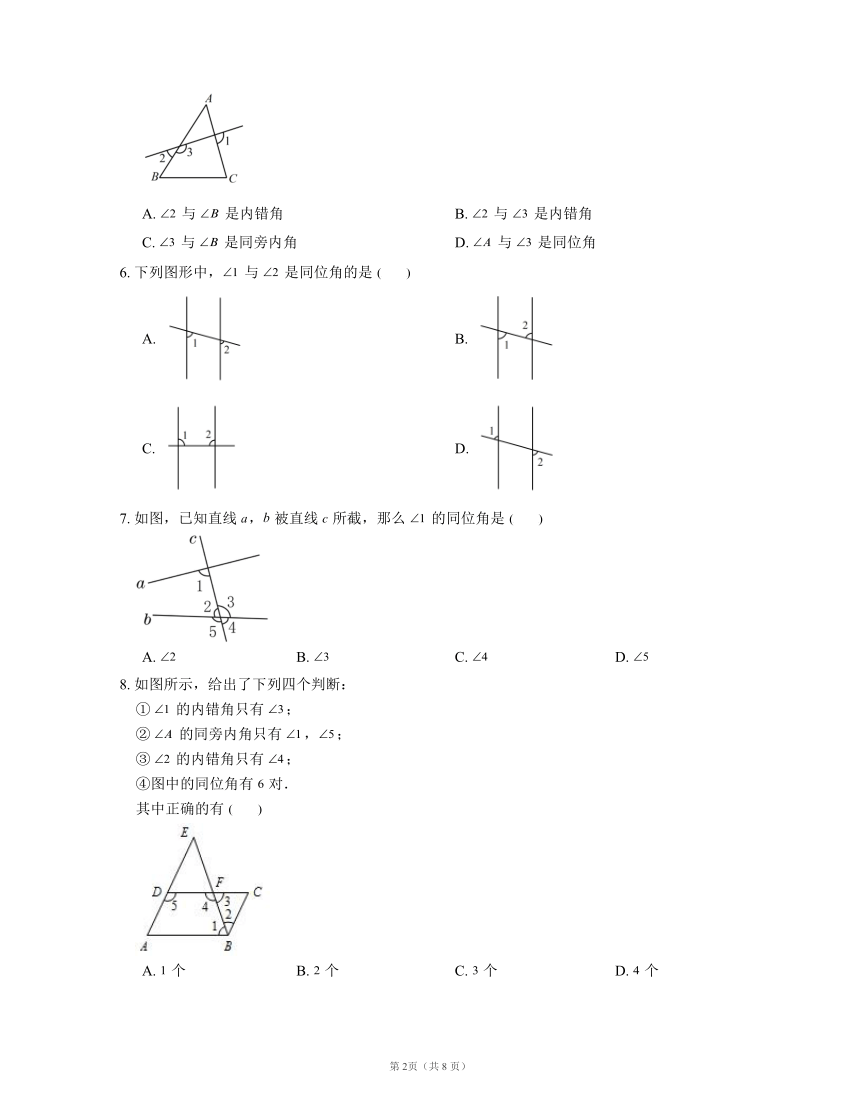
1. 在下列图形中, 与 是同位角的有
A. ①,② B. ①,③ C. ②,③ D. ②,④
2. 下列图中 和 是同位角的是
A. (1)(2)(3) B. (2)(3)(4) C. (3)(4)(5) D. (1)(2)(5)
3. 如图,与 是同位角的是
A. B. C. D.
4. 已知 与 是同旁内角.若 ,则 的度数是
A. B. C. 或 D. 不能确定
5. 如图所示,下列说法错误的是
A. 与 是内错角 B. 与 是内错角
C. 与 是同旁内角 D. 与 是同位角
6. 下列图形中, 与 是同位角的是
A. B.
C. D.
7. 如图,已知直线 , 被直线 所截,那么 的同位角是
A. B. C. D.
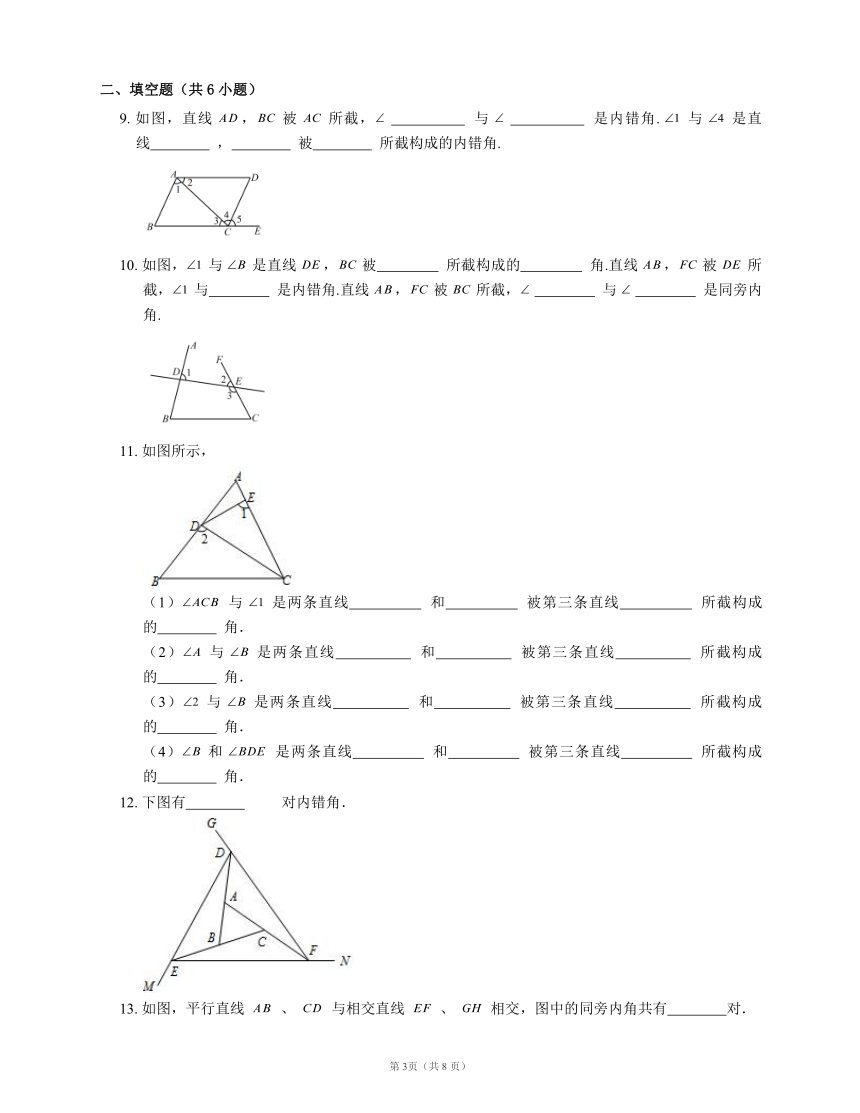
8. 如图所示,给出了下列四个判断:
① 的内错角只有 ;
② 的同旁内角只有 ,;
③ 的内错角只有 ;
④图中的同位角有 对.
其中正确的有
A. 个 B. 个 C. 个 D. 个
二、填空题(共6小题)
9. 如图,直线 , 被 所截, ? 与 ? 是内错角. 与 是直线 ? , ? 被 ? 所截构成的内错角.
10. 如图, 与 是直线 , 被 ? 所截构成的 ? 角.直线 , 被 所截, 与 ? 是内错角.直线 , 被 所截, ? 与 ? 是同旁内角.
11. 如图所示,
(1) 与 是两条直线 ? 和 ? 被第三条直线 ? 所截构成的 ? 角.
(2) 与 是两条直线 ? 和 ? 被第三条直线 ? 所截构成的 ? 角.
(3) 与 是两条直线 ? 和 ? 被第三条直线 ? 所截构成的 ? 角.
(4) 和 是两条直线 ? 和 ? 被第三条直线 ? 所截构成的 ? 角.
12. 下图有 ? 对内错角.
13. 如图,平行直线 、 与相交直线 、 相交,图中的同旁内角共有 ?对.
14. 若平面上 条直线两两相交,且无三条共线,则一共有 ?对同旁内角.
三、解答题(共6小题)
15. 图中有几对同位角?几对内错角?几对同旁内角?把它们分别写出来.
16. 如图,分别找出一个角与 配对,使这两个角成为:
①同位角;②内错角;③同旁内角.
并指出是由哪一条直线截另外哪两条直线所得.
17. 判断下列各图中的 与 是不是同位角,是的打“√”,不是的打“x”.
(1)
18. 请回答下列问题:
(1)指出下列各图中的 与 是同位角、内错角还是同旁内角.
(2)请你归纳:辨认同位角、内错角、同旁内角的方法可以是什么?
19. 如图,指出图中直线 , 被直线 所截的同位角、内错角、同旁内角.
20. (1)两条平行直线被第三条直线所截,有几对同位角,几对内错角,几对同旁内角.
(2)三条平行直线呢?四条、五条呢?
(3)你发现了什么规律.
答案
1. B
2. D 【解析】(1)图中 和 是同位角,故本项符合题意;
(2)图中 和 是同位角,故本项符合题意;
(3)图中 和 不是同位角,故本项不符合题意;
(4)图中 和 不是同位角,故本项不符合题意;
(5)图中 和 是同位角,故本项符合题意.
图中是同位角的是(1)、(2)、(5).
3. C 【解析】本题考查同位角的概念,观察图形可知 的同位角是 .
4. D 【解析】本题易忽略利用平行线性质的前提条件,因此误用平行线的性质.
本题没有说明两直线平行,因此同旁内角的数量关系是不确定的.
5. B
【解析】根据内错角、同旁内角和同位角的定义可知:A,C,D均是正确的,只有B错误.
6. A 【解析】本题考查同位角的概念.
A选项中的 和 是同位角;
B选项中的 和 是内错角;
C选项中的 和 是同旁内角;
D选项中的 和 不是我们研究的三线八角中的特殊关系.
7. D
8. A 【解析】①正确, 的同旁内角还有 ,, 的内错角还有 ,图中同位角有 对,分别是 与 , 与 , 与 , 与 , 与 , 与 , 与 , 与 .
9. ,,,,
10. ,同位,,,
11. ,,,同旁内,,,,同旁内,,,,同旁内,,,,同旁内
12.
【解析】借助内错角的概念,
可知: 与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角.
13.
【解析】图中有 条线段,所以有 对同旁内角.
14.
15. 同位角: 与 , 与 ;
内错角: 与 , 与 ;
同旁内角: 与 , 与 .
16. 如直线 与直线 被直线 所截, 与 是同位角, 与 是内错角, 与 是同旁内角.(答案不唯一)
17. (1)√;(2)×;(3)√.
【解析】提示:利用同位角的概念去判断.
18. (1) ①内错角 ②同旁内角 ③同位角 ④同位角
??????(2) 在截线的同旁找同位角和同旁内角,在截线的不同旁找内错角,因此在“三线八角”的图形中主线是截线,抓住了截线,再利用图形结构特征( 形为同位角, 形为内错角, 形为同旁内角)判断.
19. 与 , 与 是同位角;
与 , 与 是内错角;
与 是同旁内角, 与 是同旁内角.
20. (1) 两条平行直线被第三条直线所截,有 对同位角, 对内错角, 对同旁内角.
??????(2) 当有 条平行线时,有 对同位角, 对内错角, 对同旁内角;
当有 条平行线时,有 对同位角, 对内错角, 对同旁内角;
当有 条平行线时,有 对同位角, 对内错角, 对同旁内角.
??????(3) 当 条线彼此平行时,被直线 所截,即 ,
则共有 ,,, ,,,,,, 共 对平行线,每对平行线被 所截,产生 对同位角, 对内错角, 对同旁内角,则共有 对同位角, 对内错角, 对同旁内角.
第7页(共8 页)
一、选择题(共8小题)
1. 在下列图形中, 与 是同位角的有
A. ①,② B. ①,③ C. ②,③ D. ②,④
2. 下列图中 和 是同位角的是
A. (1)(2)(3) B. (2)(3)(4) C. (3)(4)(5) D. (1)(2)(5)
3. 如图,与 是同位角的是
A. B. C. D.
4. 已知 与 是同旁内角.若 ,则 的度数是
A. B. C. 或 D. 不能确定
5. 如图所示,下列说法错误的是
A. 与 是内错角 B. 与 是内错角
C. 与 是同旁内角 D. 与 是同位角
6. 下列图形中, 与 是同位角的是
A. B.
C. D.
7. 如图,已知直线 , 被直线 所截,那么 的同位角是
A. B. C. D.
8. 如图所示,给出了下列四个判断:
① 的内错角只有 ;
② 的同旁内角只有 ,;
③ 的内错角只有 ;
④图中的同位角有 对.
其中正确的有
A. 个 B. 个 C. 个 D. 个
二、填空题(共6小题)
9. 如图,直线 , 被 所截, ? 与 ? 是内错角. 与 是直线 ? , ? 被 ? 所截构成的内错角.
10. 如图, 与 是直线 , 被 ? 所截构成的 ? 角.直线 , 被 所截, 与 ? 是内错角.直线 , 被 所截, ? 与 ? 是同旁内角.
11. 如图所示,
(1) 与 是两条直线 ? 和 ? 被第三条直线 ? 所截构成的 ? 角.
(2) 与 是两条直线 ? 和 ? 被第三条直线 ? 所截构成的 ? 角.
(3) 与 是两条直线 ? 和 ? 被第三条直线 ? 所截构成的 ? 角.
(4) 和 是两条直线 ? 和 ? 被第三条直线 ? 所截构成的 ? 角.
12. 下图有 ? 对内错角.
13. 如图,平行直线 、 与相交直线 、 相交,图中的同旁内角共有 ?对.
14. 若平面上 条直线两两相交,且无三条共线,则一共有 ?对同旁内角.
三、解答题(共6小题)
15. 图中有几对同位角?几对内错角?几对同旁内角?把它们分别写出来.
16. 如图,分别找出一个角与 配对,使这两个角成为:
①同位角;②内错角;③同旁内角.
并指出是由哪一条直线截另外哪两条直线所得.
17. 判断下列各图中的 与 是不是同位角,是的打“√”,不是的打“x”.
(1)
18. 请回答下列问题:
(1)指出下列各图中的 与 是同位角、内错角还是同旁内角.
(2)请你归纳:辨认同位角、内错角、同旁内角的方法可以是什么?
19. 如图,指出图中直线 , 被直线 所截的同位角、内错角、同旁内角.
20. (1)两条平行直线被第三条直线所截,有几对同位角,几对内错角,几对同旁内角.
(2)三条平行直线呢?四条、五条呢?
(3)你发现了什么规律.
答案
1. B
2. D 【解析】(1)图中 和 是同位角,故本项符合题意;
(2)图中 和 是同位角,故本项符合题意;
(3)图中 和 不是同位角,故本项不符合题意;
(4)图中 和 不是同位角,故本项不符合题意;
(5)图中 和 是同位角,故本项符合题意.
图中是同位角的是(1)、(2)、(5).
3. C 【解析】本题考查同位角的概念,观察图形可知 的同位角是 .
4. D 【解析】本题易忽略利用平行线性质的前提条件,因此误用平行线的性质.
本题没有说明两直线平行,因此同旁内角的数量关系是不确定的.
5. B
【解析】根据内错角、同旁内角和同位角的定义可知:A,C,D均是正确的,只有B错误.
6. A 【解析】本题考查同位角的概念.
A选项中的 和 是同位角;
B选项中的 和 是内错角;
C选项中的 和 是同旁内角;
D选项中的 和 不是我们研究的三线八角中的特殊关系.
7. D
8. A 【解析】①正确, 的同旁内角还有 ,, 的内错角还有 ,图中同位角有 对,分别是 与 , 与 , 与 , 与 , 与 , 与 , 与 , 与 .
9. ,,,,
10. ,同位,,,
11. ,,,同旁内,,,,同旁内,,,,同旁内,,,,同旁内
12.
【解析】借助内错角的概念,
可知: 与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角;
与 成内错角.
13.
【解析】图中有 条线段,所以有 对同旁内角.
14.
15. 同位角: 与 , 与 ;
内错角: 与 , 与 ;
同旁内角: 与 , 与 .
16. 如直线 与直线 被直线 所截, 与 是同位角, 与 是内错角, 与 是同旁内角.(答案不唯一)
17. (1)√;(2)×;(3)√.
【解析】提示:利用同位角的概念去判断.
18. (1) ①内错角 ②同旁内角 ③同位角 ④同位角
??????(2) 在截线的同旁找同位角和同旁内角,在截线的不同旁找内错角,因此在“三线八角”的图形中主线是截线,抓住了截线,再利用图形结构特征( 形为同位角, 形为内错角, 形为同旁内角)判断.
19. 与 , 与 是同位角;
与 , 与 是内错角;
与 是同旁内角, 与 是同旁内角.
20. (1) 两条平行直线被第三条直线所截,有 对同位角, 对内错角, 对同旁内角.
??????(2) 当有 条平行线时,有 对同位角, 对内错角, 对同旁内角;
当有 条平行线时,有 对同位角, 对内错角, 对同旁内角;
当有 条平行线时,有 对同位角, 对内错角, 对同旁内角.
??????(3) 当 条线彼此平行时,被直线 所截,即 ,
则共有 ,,, ,,,,,, 共 对平行线,每对平行线被 所截,产生 对同位角, 对内错角, 对同旁内角,则共有 对同位角, 对内错角, 对同旁内角.
第7页(共8 页)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
