浙教版七年级数学下册1.4 平行线的性质同步练习含答案
文档属性
| 名称 | 浙教版七年级数学下册1.4 平行线的性质同步练习含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 569.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-20 09:05:01 | ||
图片预览


文档简介
1.4 平行线的性质
一、选择题(共8小题)
1. 如图所示,已知 , 平分 ,,则 的度数为
A. B. C. D.
2. 如图,, 平分 ,且 ,则 的度数为
A. B. C. D.
3. 如图,, 分别为交 , 于点 ,,,则 的度数为
A. B. C. D.
4. 如图,直线 ,直线 分别与 , 相交,,则 的度数为
A. B. C. D.
5. 如图, 被平行直线 , 所截,若 ,,则 的度数是
A. B. C. D.
6. 如图所示,已知 ,则表示 的式子是
A. B.
C. D.
7. 如图所示,两直线 、 平行,则
A. B. C. D.
8. 同一平面内的四条直线若满足 ,,,则下列式子成立的是
A. B. C. D.
二、填空题(共6小题)
9. 如图,若 ,,,则 ?.
10. 如图,,,,则 ? 度.
11. 如图,已知 ,则 ?.
12. 如图所示,, 平分 ,,则 + ?, ?.
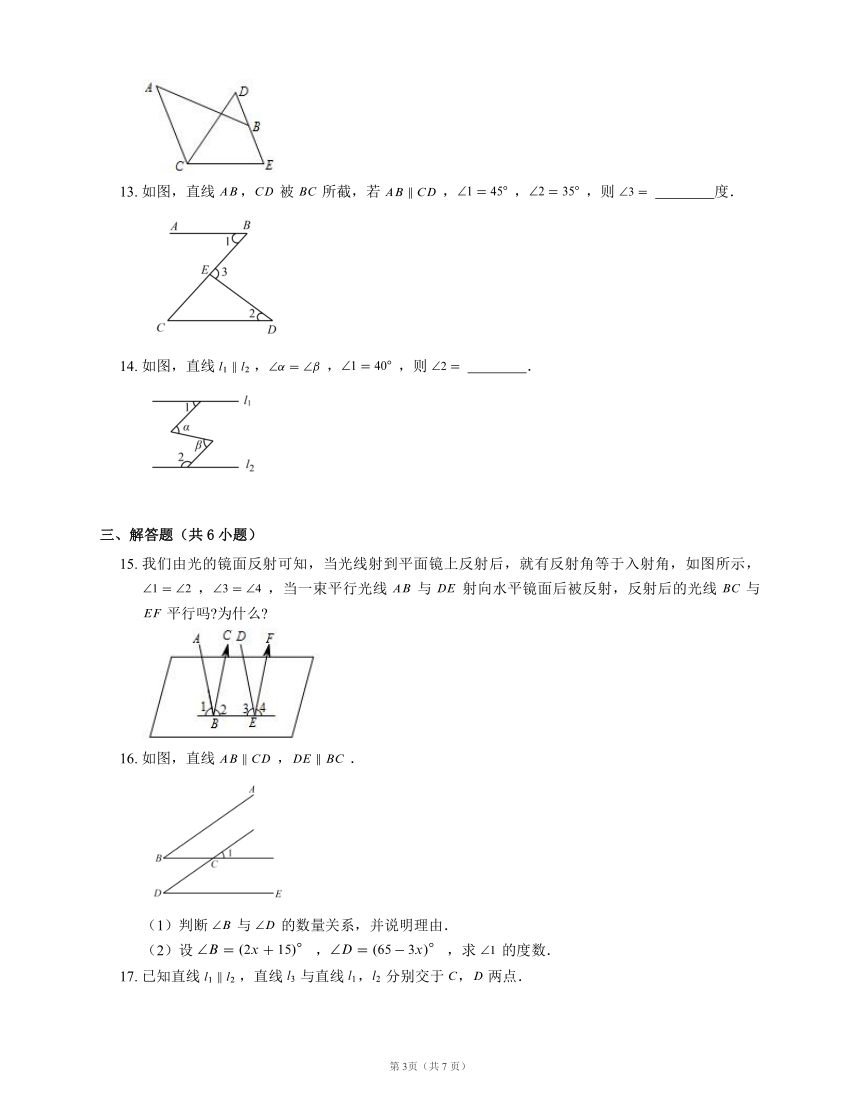
13. 如图,直线 , 被 所截,若 ,,,则 ?度.
14. 如图,直线 ,,,则 ?.
三、解答题(共6小题)
15. 我们由光的镜面反射可知,当光线射到平面镜上反射后,就有反射角等于入射角,如图所示,,,当一束平行光线 与 射向水平镜面后被反射,反射后的光线 与 平行吗?为什么?
16. 如图,直线 ,.
(1)判断 与 的数量关系,并说明理由.
(2)设 ,,求 的度数.
17. 已知直线 ,直线 与直线 , 分别交于 , 两点.
(1)如图 ①,有一动点 在线段 之间运动(不与 , 两点重合),问在点 的运动过程中是否始终具有 这一相等关系?试说明理由.
(2)如图 ②,当动点 在线段 之外运动(不与 , 两点重合),问上述结论是否还成立?若不成立,试写出新的结论并说明理由.
18. 如图,,,.求 的度数.
19. 如图,已知:,, 于 ,试问 与 垂直吗?请说明理由.
20. 如图①,,,,.这是一个有用的事实,请用这个事实,在图②中的四边形 内引一条和边平行的直线.
(1)求出 的度数.
1. C
2. A
3. C
4. B
5. D
6. C 【解析】过点 作 .
则 ,所以 ,,则 ,所以 .
7. D 【解析】提示:分别过 ,,, 点作 的平行线,再求各个角度的和.
8. C 【解析】直线 ,,, 的位置关系如图所示.
9.
10.
11.
12. ,
【解析】,
,
,.
,
,
,
.
13.
14.
【解析】
,
.
,
.
.
.
15. .
理由如下:
,
(两直线平行,同位角相等).
又 ,,
.
(同位角相等,两直线平行).
16. (1) .
,
.
,
.
.
??????(2) 由 ,
解得 ,
所以 .
所以 .
17. (1) 成立.理由如下:
如图,过点 作 ,则 .
,
.
.
,
.
??????(2) 不成立,新的结论为 .理由如下:
如图,过点 作 ,则 .
,
.
.
,
.
18. 因为 , ,
所以 .
因为 ,
所以 .
所以 .
19. .理由:
,
.
.
,
.
.
.
,
.
.
.
20. 过点 作 交 于点 ,则 , .
由题意,得 ,
第7页(共7 页)
一、选择题(共8小题)
1. 如图所示,已知 , 平分 ,,则 的度数为
A. B. C. D.
2. 如图,, 平分 ,且 ,则 的度数为
A. B. C. D.
3. 如图,, 分别为交 , 于点 ,,,则 的度数为
A. B. C. D.
4. 如图,直线 ,直线 分别与 , 相交,,则 的度数为
A. B. C. D.
5. 如图, 被平行直线 , 所截,若 ,,则 的度数是
A. B. C. D.
6. 如图所示,已知 ,则表示 的式子是
A. B.
C. D.
7. 如图所示,两直线 、 平行,则
A. B. C. D.
8. 同一平面内的四条直线若满足 ,,,则下列式子成立的是
A. B. C. D.
二、填空题(共6小题)
9. 如图,若 ,,,则 ?.
10. 如图,,,,则 ? 度.
11. 如图,已知 ,则 ?.
12. 如图所示,, 平分 ,,则 + ?, ?.
13. 如图,直线 , 被 所截,若 ,,,则 ?度.
14. 如图,直线 ,,,则 ?.
三、解答题(共6小题)
15. 我们由光的镜面反射可知,当光线射到平面镜上反射后,就有反射角等于入射角,如图所示,,,当一束平行光线 与 射向水平镜面后被反射,反射后的光线 与 平行吗?为什么?
16. 如图,直线 ,.
(1)判断 与 的数量关系,并说明理由.
(2)设 ,,求 的度数.
17. 已知直线 ,直线 与直线 , 分别交于 , 两点.
(1)如图 ①,有一动点 在线段 之间运动(不与 , 两点重合),问在点 的运动过程中是否始终具有 这一相等关系?试说明理由.
(2)如图 ②,当动点 在线段 之外运动(不与 , 两点重合),问上述结论是否还成立?若不成立,试写出新的结论并说明理由.
18. 如图,,,.求 的度数.
19. 如图,已知:,, 于 ,试问 与 垂直吗?请说明理由.
20. 如图①,,,,.这是一个有用的事实,请用这个事实,在图②中的四边形 内引一条和边平行的直线.
(1)求出 的度数.
1. C
2. A
3. C
4. B
5. D
6. C 【解析】过点 作 .
则 ,所以 ,,则 ,所以 .
7. D 【解析】提示:分别过 ,,, 点作 的平行线,再求各个角度的和.
8. C 【解析】直线 ,,, 的位置关系如图所示.
9.
10.
11.
12. ,
【解析】,
,
,.
,
,
,
.
13.
14.
【解析】
,
.
,
.
.
.
15. .
理由如下:
,
(两直线平行,同位角相等).
又 ,,
.
(同位角相等,两直线平行).
16. (1) .
,
.
,
.
.
??????(2) 由 ,
解得 ,
所以 .
所以 .
17. (1) 成立.理由如下:
如图,过点 作 ,则 .
,
.
.
,
.
??????(2) 不成立,新的结论为 .理由如下:
如图,过点 作 ,则 .
,
.
.
,
.
18. 因为 , ,
所以 .
因为 ,
所以 .
所以 .
19. .理由:
,
.
.
,
.
.
.
,
.
.
.
20. 过点 作 交 于点 ,则 , .
由题意,得 ,
第7页(共7 页)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
