3.3 多项式的乘法 导学案（无答案）

3.3 多项式的乘法 导学案
一、学习目标
1、掌握多项式与多项式相乘的法则.
2、会运用单项式与单项式、单项式与多项式、多项式与多项式相乘的法则化简整式
二、回顾预习
1、填空：
(1)(－x)·(－x)·(－x) =______; (2) (x)=_______; (3) (xy)=______; (4)(xy)·(xy)·(xy) =______; (5) (－3xy)(－5xyz)= ;
(6)（b－3a）(－4a+3ab) =________________
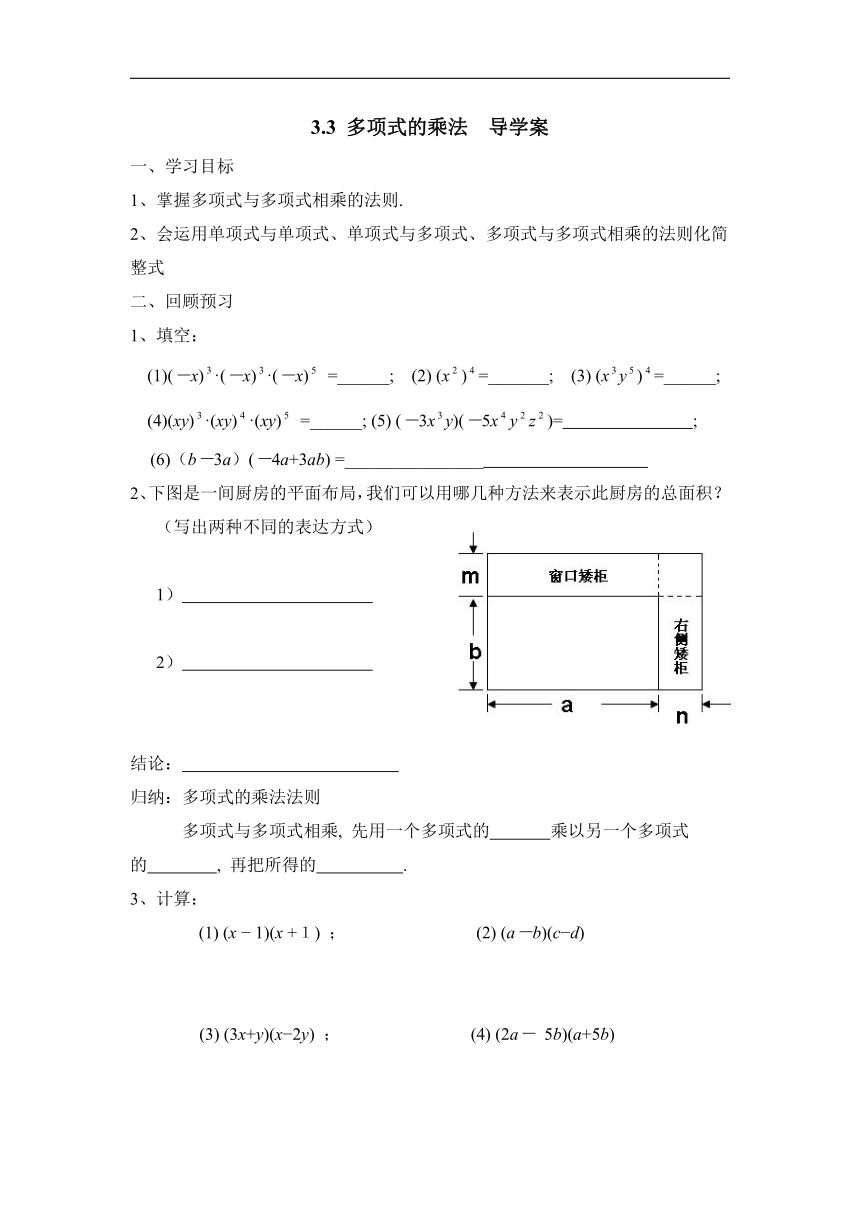
2、下图是一间厨房的平面布局，我们可以用哪几种方法来表示此厨房的总面积？
（写出两种不同的表达方式）
1）
2）
结论：
归纳：多项式的乘法法则
多项式与多项式相乘, 先用一个多项式的 乘以另一个多项式的 , 再把所得的 .
3、计算：
(1) (x ? 1)(x +１) ； (2) (a－b)(c?d)
(3) (3x+y)(x?2y) ； (4) (2a－ 5b)(a+5b)
三、巩固练习
1、计算：(1) (2)
2、先化简，再求值：X=
四、拓展提高
1、观察下列各式的计算结果与相乘的两个多项式之间的关系：
(x+2)(x+3)=x+5x+6 ；(x+4)(x+2)=x+6x+8 ；(x+6)(x+5)=x+11x+30
(1)你发现有什么规律？按你发现的规律填空：
(x+3)(x+5)=x+(____+____)x +____×_____
(2)你能很快说出与(x+a)(x+b)相等的多项式吗？先猜一猜，再用多项式相乘的运算法则验证.
2、计算(x+2x－3x－5)(2x－3x+x－2)时,若不展开,求出x项的系数.
3、已知，
求的值.