1.3平行线的判定 强化提升训练 解析版

初中数学浙教版七年级下册1.3平行线的判定 强化提升训练
一、单选题
1.如图所示，在下列四组条件中，能判定AB∥CD的是（ ??）

A.?∠1＝∠2???????????????????B.?∠ABD＝∠BDC???????????????????C.?∠3＝∠4???????????????????D.?∠BAD+∠ABC＝180°
2.如图所示，下列条件中，不能判断AD∥BC的是（?? ）
A.?∠1＝∠4??????????????????????B.?∠3＝∠4??????????????????????C.?∠2+∠3＝180°??????????????????????D.?∠1+∠D＝180°
3.如图,不能作为判断AE∥CD的条件的是(??? )
A.?∠FEB=∠ECD??????????????B.?∠AEC=∠ECD??????????????C.?∠BEC+∠ECD=180°??????????????D.?∠AEG=∠DCH??
4.下列图形中，由∠1＝∠2能得到AB∥CD的是（?? ）

A???? ?B C????????????????? ?D版权所有：21教育】
5.如图，若 ，则 ，判断依据是(?? ?)
A.?两直线平行，同位角相等????????????????????????????????????B.?两直线平行，内错角相等C.?同位角相等，两直线平行????????????????????????????????????D.?内错角相等，两直线平行21*cnjy*com
6.下面四种沿AB折叠的方法中，能判定纸带两条边线a，b互相平行的是(??? )

①如图7-1，展开后测得∠1=∠2;②如图7-2，展开后测得∠1=∠2，∠3=∠4;
③如图7-3，测得∠1=70°，∠2=55°;④如图7-4，测得∠1=∠2
A.?①③?????????????????????????????????B.?①②③?????????????????????????????????C.?①④?????????????????????????????????D.?①②③④
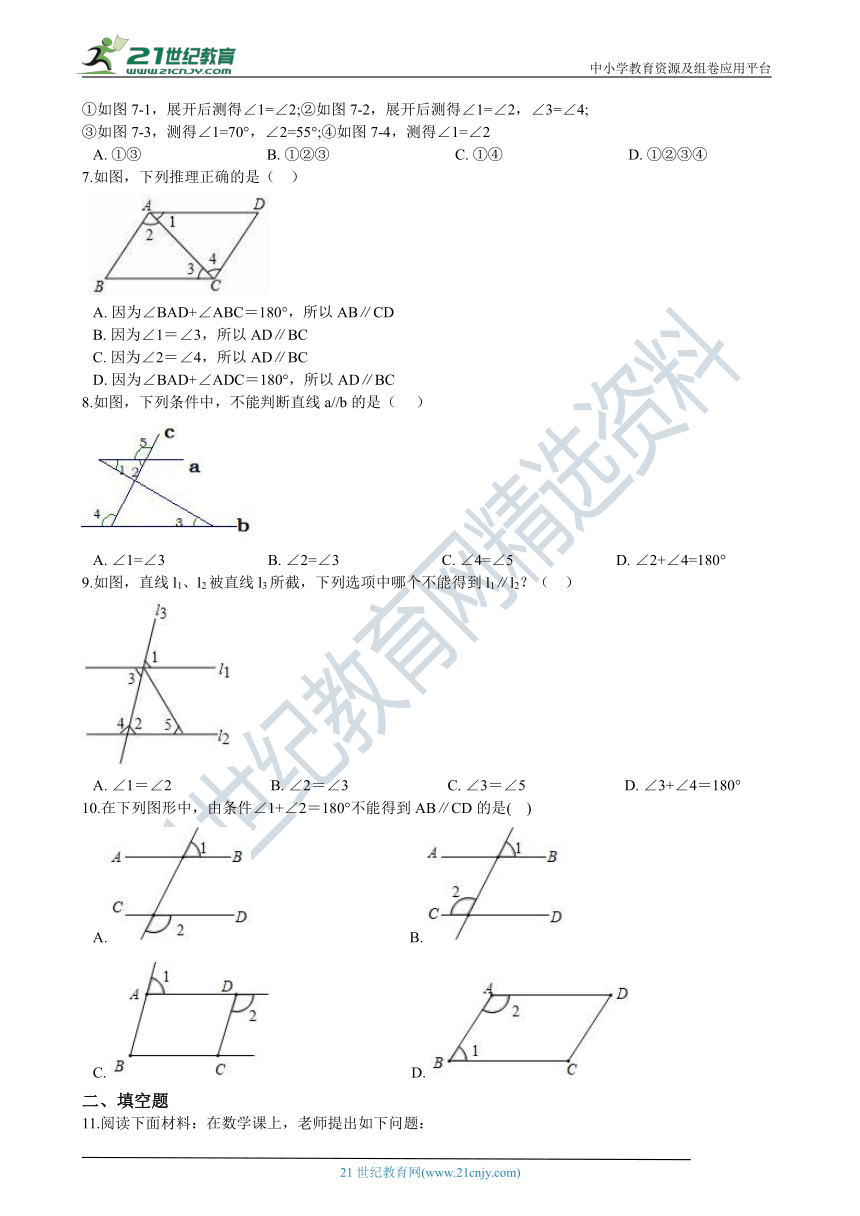
7.如图，下列推理正确的是（ ??）

A.?因为∠BAD+∠ABC＝180°，所以AB∥CDB.?因为∠1＝∠3，所以AD∥BCC.?因为∠2＝∠4，所以AD∥BCD.?因为∠BAD+∠ADC＝180°，所以AD∥BC21教育网
8.如图，下列条件中，不能判断直线a//b的是（??? ）
A.?∠1=∠3???????????????????????????B.?∠2=∠3???????????????????????????C.?∠4=∠5???????????????????????????D.?∠2+∠4=180°
9.如图，直线l1、l2被直线l3所截，下列选项中哪个不能得到l1∥l2？（?? ）
A.?∠1＝∠2??????????????????????????B.?∠2＝∠3??????????????????????????C.?∠3＝∠5??????????????????????????D.?∠3+∠4＝180°
10.在下列图形中，由条件∠1+∠2＝180°不能得到AB∥CD的是( ??) 2-1-c-n-j-y
A.???????????????????????????????????????????B.?C.??????????????????????????????????????D.?
二、填空题
11.阅读下面材料：在数学课上，老师提出如下问题：
作图：过直线外一点作已知直线的平行线．
已知：直线l及其外一点A(如图1)．
求作：l的平行线，使它经过点A ．
小凡利用两块形状相同的三角尺进行如下操作：
如图2所示：
⑴用第一块三角尺的一条边贴住直线l ， 第二块三角尺的一条边紧靠第一块三角尺；
⑵将第二块三角尺沿第一块三角尺移动，使其另一边经过点A ， 沿这边作出直线AB ， 所以，直线AB即为所求．
老师说：“小凡的作法正确”
请回答：小凡的作图依据是________．
12.如图，请添加一个条件，使AB∥CD，那么添加的条件是________．
13.一副直角三角尺如图①叠放，现将45°的三角尺ADE固定不动，将含30°的三角尺ABC绕顶点A顺时针转动，要求两块三角尺的一组边互相平行.如图②，当∠BAD=15°时，有一组边BC∥DE，请再写出两个符合要求的∠BAD（0°＜∠BAD＜180°）的度数________.
14.如图，若∠1=100°，∠4=80°，可得到________，理由是________；若∠3=70°，则∠2=________时，也可推出AB∥CD．
15.已知，如图AC、BD相交于点O，∠A=63°，∠D=42°，则∠B+∠C≠________度，AB不平行DC．
三、解答题
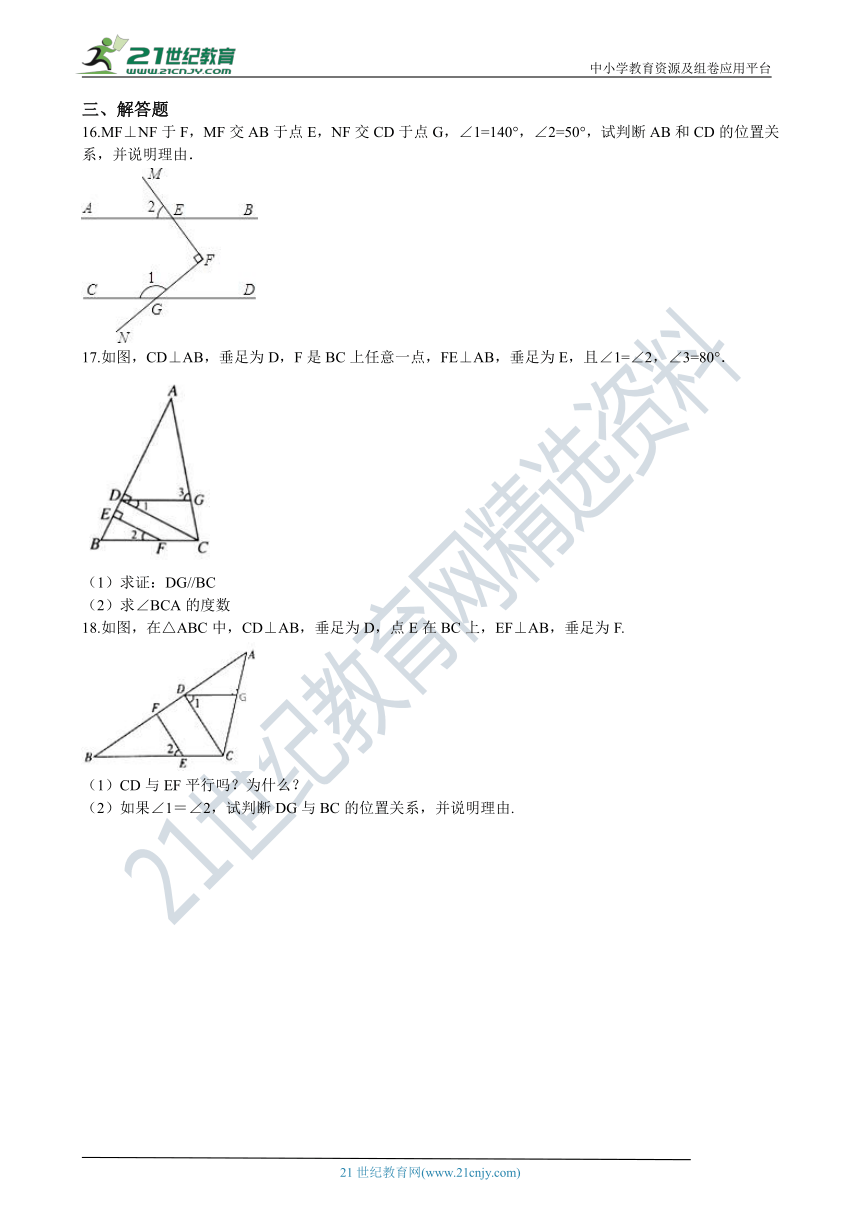
16.MF⊥NF于F，MF交AB于点E，NF交CD于点G，∠1=140°，∠2=50°，试判断AB和CD的位置关系，并说明理由．
17.如图，CD⊥AB，垂足为D，F是BC上任意一点，FE⊥AB，垂足为E，且∠1=∠2，∠3=80°．

（1）求证：DG//BC
（2）求∠BCA的度数
18.如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F.
（1）CD与EF平行吗？为什么？
（2）如果∠1＝∠2，试判断DG与BC的位置关系，并说明理由.
答案解析部分
一、单选题
1. B
解：A、∵∠1=∠2，∴ AD∥BC，不符合题意； B、??∵∠ABD＝∠BDC?，∴AB∥CD，符合题意； C、∵ ∠3＝∠4 ，∴ AD∥BC，不符合题意； D、∵ ∠BAD+∠ABC＝180°?，∴AD∥BC，不符合题意； 故答案为：B. 【分析】根据平行线的性质，即同位角相等两直线平行，内错角相等两直线平行，同旁内角互补两直线平行，逐项分析判断即可.
2. A
解：A、∵∠1＝∠4，∴AB∥CD（内错角相等，两直线平行），但不能判定AD∥BC；
B、∵∠3＝∠4，∴AD∥BC（同位角相等，两直线平行）；
C、∵∠2+∠3＝180°，∴AD∥BC（同旁内角互补，两直线平行）；
D、∵∠1+∠D＝180°，∴AD∥BC（同旁内角互补，两直线平行）；
故答案为：A.
【分析】A、∠1与∠4是直线DC,AB被BC所截的一对内错角，根据内错角相等，二直线平行得出AB∥CD，但不能判定AD∥BC,A符合题意； B、∠3与∠4是直线DA,CB被BA所截的一对同位角，根据同位角相等，二直线平行得出AD∥CB，B不符合题意; C、∠3与∠2是直线DA,CB被BA所截的一对同旁内角，根据同旁内角互补，二直线平行得出AD∥CB，B不符合题意; D、∠1与∠D是直线DA,CB被DC所截的一对同旁内角，根据同旁内角互补，二直线平行得出AD∥CB，B不符合题意，综上所述就可得出答案.www-2-1-cnjy-com
3. D
解：A、 ∠FEB=∠ECD ，则AE∥CD（同位角相等两直线平行），正确，不符合题意； B、 ∠AEC=∠ECD ，则AE∥CD（内错角相等两直线平行），正确，不符合题意； C、 ∠BEC+∠ECD=180° ，则AE∥CD（同旁内角互补两直线平行），正确，不符合题意； D、 ∠AEG和∠DCH不属于三线八角当中的一组角，不能用来判断是否平行，错误，符合题意； 故答案为：D. 【分析】利用平行线的判定定理，即同位角相等两直线平行，内错角相等两直线平行，同旁内角互补两直线平行，逐一判断即可。
4. B
解：A、∠1、∠2是同旁内角，由∠1=∠2不能判定AB∥CD；
B、∠1、∠2是内错角，由∠1=∠2能判定AB∥CD；
C、∠1、∠2是内错角，由∠1=∠2能判定AD∥BC，不能判定AB∥CD；
D，∠1、∠2是同旁内角，由∠1=∠2不能判定AB∥CD；
故答案为：B． 【分析】根据同位角，内错角，同旁内角的概念和平行线的判定方法，即可.
5. D
解：∵ 互为内错角,且 ，
∴AB∥CD ( 内错角相等，两直线平行 )。
故答案为：D。
【分析】根据图形可知， 互为内错角，又它们相等，故根据 内错角相等，两直线平行 即可得出结论。21世纪教育网版权所有
6. B
解：①∵∠1=∠2， ∴a∥b（内错角相等，两直线平行），故符合题意； ②∵ ∠1=∠2，∠3=∠4， ∴∠1=∠2=∠3=∠4=90°， ∴a∥b,故符合题意； ③∵∠1+2∠2=180°， ∴a∥b（同旁内角互补，两直线平行）. ④由∠1=∠2，无法判断a、b平行. 故答案为：B. 21cnjy.com
【分析】根据内错角相等，两直线平行可得a∥b，据此判断①；根据折叠的性质及同旁内角互补，两直线平行可得a∥b，据此判断②③；④由∠1=∠2，无法判断a、b平行.【来源：21cnj*y.co*m】
7. B
解：A：因为∠BAD+∠ABC＝180°，所以AD∥BC，不符合题意； B、因为∠1＝∠3，所以AD∥BC，符合题意； C、 因为∠2＝∠4，所以AB∥DC，不符合题意； D、 因为∠BAD+∠ADC＝180°，所以AB∥DC，不符合题意；
故答案为：B. ?
【分析】AD根据同旁内角互补两直线平行，BC根据内错角相等两直线平行，分别分析判断。
8. B
解：当∠1=∠3时，a∥b；
当∠4=∠5时，a∥b；
当∠2+∠4=180°时，a∥b.
故答案为：B.
【分析】A项根据内错角相等，两直线平行判断；B项无法判定a∥b；C项根据同位角相等，两直线平行；D项根据同旁内角互补，两直线平行。【出处：21教育名师】
9. C
解： 、 ， ，故本选项不合题意；
、 ， ，故本选项不合题意；
、 不能判定 ，故本选项符合题意；
、 ， ，故本选项不合题意．
故答案为： ． 【分析】平行线的3种判定方法：1.同位角相等，两直线平行；2.内错角相等，两直线平行；3.同旁内角互补，两直线平行。21·世纪*教育网
10. D
解：A、∠1的对顶角与∠2的对顶角是同旁内角，它们互补，所以能判定AB∥CD；
B、∠1的对顶角与∠2是同旁内角，它们互补，所以能判定AB∥CD；
C、∠1的邻补角∠BAD＝∠2，所以能判定AB∥CD；
D、由条件∠1+∠2＝180°能得到AD∥BC，不能判定AB∥CD；
故答案为：D.
【分析】在三线八角的前提下，同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行.据此判断即可.
二、填空题
11. 内错角相等，两直线平行
解：由图可知， 与 是一对内错角，且 ，
直线 （内错角相等，两直线平行）.
故答案为：内错角相等，两直线平行.
【分析】这是一道阅读理解题。认真读题，发现其中的原理和依据：内错角相等，两直线平行.
12. ∠1＝∠4（答案不唯一）
解：∠1=∠4， 则AB∥CD, 故可添加条件为∠1=∠4； 【分析】由于内错角相等两直线平行，要使AB∥CD，可填条件∠1=∠4，∠3=∠2；另外也可根据同旁内角互补两直线平行，添加条件。
13. 45°，60，105°，135°
解：（1）当∠BAD=45°时，如图，
∵∠BAD=45°，∠BAC=90°，
∴∠CAF=45°，
∴∠D=∠CAF=45°，
∴DE∥AC；
（ 2 ）当∠BAD=60°时，如图分类讨论：
当∠BAD=60°时，
∴∠B=∠BAD=60°，
∴BC∥AD；
（ 3 ）当∠BAD=105°时，如图，
即∠BAD=∠BAE+∠EAD=105°，
∴∠BAE=∠BAD-∠EAD=105°-45°=60°，
∴∠BAE=∠B=60°，
∴BC∥AE；
（ 4 ）当∠BAD=135°时，如图，
则∠EAB=∠BAD-∠EAD=135°-45°=90°.
∴∠EAB=∠E=90°，
∴AB∥DE.综上所述，当∠BAD为： 45°，60，105°，135° 时， 两块三角尺的一组边互相平行 。 故答案为： 45°，60，105°，135°www.21-cn-jy.com
【分析】（1）当∠BAD=45°时，如图，根据学具的性质得出∠BAD=45°，∠BAC=90°，根据平角的定义得出∠CAF=45°，故∠D=∠CAF=45°，根据同位角相等，二直线平行得出DE∥AC；（2）当∠BAD=60°时，如图，根据学具的性质得出∠B=60°，故∠B=∠BAD=60°，根据内错角相等，二直线平行得出BC∥AD；（ 3 ）当∠BAD=105°时，如图，根据学具的性质及角的和差得出∠BAE=∠BAD-∠EAD=105°-45°=60°，故∠BAE=∠B=60°，根据内错角相等，二直线平行得出BC∥AD；（ 4 ）当∠BAD=135°时，如图，根据学具的性质及角的和差得出∠EAB=∠BAD-∠EAD=135°-45°=90°，故∠EAB=∠E=90°，根据内错角相等，二直线平行得出AB∥DE.2·1·c·n·j·y
14.AB∥CD；同旁内角互补，两直线平行；110°
解：∵∠1=100°，∠4=80°，∴∠1+∠4=180°，∴AB∥CD；∵∠3=70°，则∠2=110，∴∠2+∠3=180°，∴AB∥CD．故答案为AB∥CD，同旁内角互补，两直线平行；110°．【分析】∠1和∠4，∠2和∠3是同旁内角，根据同旁内角互补，两直线平行，都能得出AB∥CD，
15.105
解：∵AB不平行DC，∴∠C≠∠A，∠B≠∠D，∴∠B+∠C≠63°+42°，即∠B+∠C≠105°．【分析】根据平行线的判定方法可知当∠C≠∠A，∠B≠∠D时，则AB不平行DC，即可得出结论。
三、解答题
16.解:延长MF交CD于点H∠1=90∠FH,2140∴∠CHF=1405-902=50°,∠CHF=∠2,AB∥CD 【来源：21·世纪·教育·网】
【分析】延长MF交CD于点H，根据已知条件可证得∠CHF=∠2,再根据同位角相等，两直线平行可证明AB∥CD。21*cnjy*com
17. （1）证明:CD⊥AB,FE⊥AB(已知)
CD∥EF(垂直于同一直线的两直线平行），
∠2=∠BCD(两直线平行，同位角相等），
∠1=∠2(已知），
∠1=∠BCD（等量代换）
BC∥DG(内错角相等，两直线平行）；．

（2）解：DG∥BC(已证)，
∠3=∠BCG(两直线平行，同位角相等），
∠3=80°(已知），
∠BCA=80°（等量代换）．
【分析】（1）根据内错角相等，可证两直线平行。 （2）根据同位角相等，可换算得到∠BCA的度数。21教育名师原创作品
18.（1）解：在△ABC中，∵CD⊥AB，垂足为D，点E在BC上，EF⊥AB； ；∴CD//EF（同位角相等，两直线平行）（2）解：由（1）知CD//EF，得 （两直线平行，同位角相等）；如果∠1=∠2；那么 ；所以DG‖BC （内错角相等，两直线平行）
【分析】本题考察平行线的知识，会判断两直线平行是解本题的关键，考生要掌握判断两直线平行的方法21·cn·jy·com