1.3.2 平行线的判定(知识清单+经典例题+夯实基础+提优特训+中考链接)
文档属性
| 名称 | 1.3.2 平行线的判定(知识清单+经典例题+夯实基础+提优特训+中考链接) |  | |
| 格式 | zip | ||
| 文件大小 | 367.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-20 18:00:03 | ||
图片预览



文档简介
浙江版2019-2020学年度下学期七年级数学下册第1章平行线
1.3平行线的判定(2)
【知识清单】
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单地说,内错角相等,两直线平行.
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单地说,同旁内角互补,两直线平行.
【经典例题】
例题1.如图,下列说法中,正确的是( )
A.若∠3=∠6,则AB∥CD
B.若∠2=∠4,则AB∥CD
C.若∠DAB+∠ABC=180°,则AB∥CD
D.若∠1=∠5,则AB∥CD
【考点】平行线的判定.
【分析】根据平行线的判定,结合图形对选项一一分析,排除错误答案.
【解答】A、若∠3=∠6,不能判定AB∥CD,故选项错误;
B、若∠2=∠4,则AB∥CD,故选项错误;
C、若∠DAB+∠ABC=180°,则AB∥CD,故选项错误;
D、若∠1=∠5,则AB∥CD,故选项正确.
故选D.
【点评】正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,切记只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
例题2.完成下面的证明:
已知:如图.BE平分∠ABC,CE平分∠BCD,若∠1+∠2=90°.求证:AB∥CD.
证明:∵BE平分∠ABC( ),
∴∠ABC =2∠1( ).
∵CE平分∠BCD( ),
∴∠BCD =2 ( ).
∴∠ABC +∠BCD =2∠1+2∠2=2(∠1+∠2)( ).
∵∠1+∠2=90°( ),
∴∠ABC+∠BCD= ( ).
∴AB∥CD( ).
【考点】平行线的判定.?
【分析】首先根据角平分线的定义可得∠ABC=2∠1,∠BCD=2∠2,根据等量代换可
∠ABC +∠BCD =2∠1+2∠2=2(∠1+∠2),进而得到∠ABC+∠BCD =180°,然后再根据同旁内角互补两直线平行可得答案.
【解答】在参考答案里
【点评】此题主要考查了平行线的判定,关键是掌握角平分线定义和平行线的判定方法.
【夯实基础】
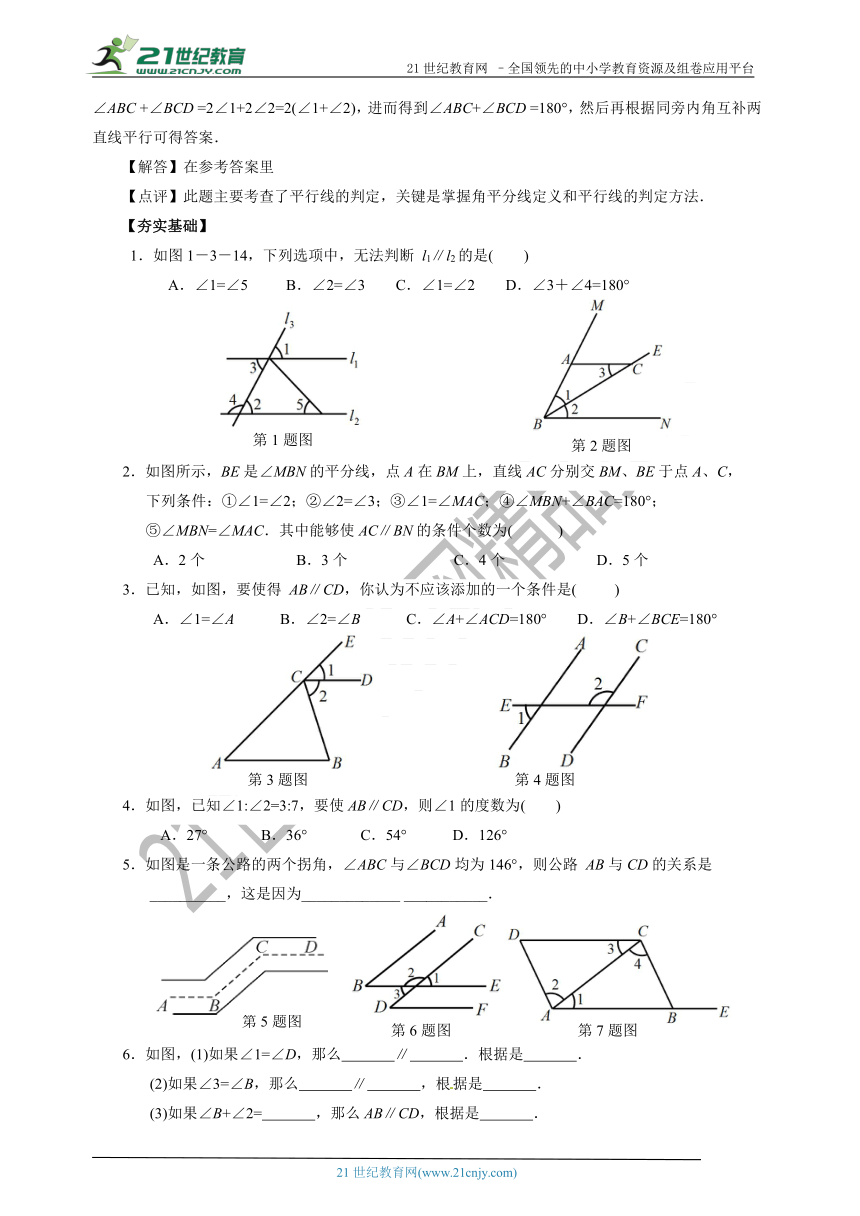
1.如图1-3-14,下列选项中,无法判断 l1∥l2的是( )
A.∠1=∠5 B.∠2=∠3 C.∠1=∠2 D.∠3+∠4=180°
2.如图所示,BE是∠MBN的平分线,点A在BM上,直线AC分别交BM、BE于点A、C,
下列条件:①∠1=∠2;②∠2=∠3;③∠1=∠MAC;④∠MBN+∠BAC=180°;
⑤∠MBN=∠MAC.其中能够使AC∥BN的条件个数为( )
A.2个 B.3个 C.4个 D.5个
3.已知,如图,要使得 AB∥CD,你认为不应该添加的一个条件是( )
A.∠1=∠A B.∠2=∠B C.∠A+∠ACD=180° D.∠B+∠BCE=180°
4.如图,已知∠1:∠2=3:7,要使AB∥CD,则∠1的度数为( )
A.27° B.36° C.54° D.126°
5.如图是一条公路的两个拐角,∠ABC与∠BCD均为146°,则公路 AB与CD的关系是
__________,这是因为_____________ ___________.
6.如图,(1)如果∠1=∠D,那么 ∥ .根据是 .
(2)如果∠3=∠B,那么 ∥ ,根据是 .
(3)如果∠B+∠2= ,那么AB∥CD,根据是 .
7.如图,点E在AB的延长线上,下列四个条件:①∠1=∠3;②∠2=∠4;③∠DAB=∠CBE;④∠D+∠BCD=180°.其中能判断AD∥CB的是 (填写正确的序号即可).
8.如图,已知CD⊥DA,DA⊥AB,∠1=∠4.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
证明:∵ ,
∴∠CDA=90°,∠DAB=90° ( ).
∴∠4+∠3=90°,∠2+∠1=90°.
又∵∠1=∠4,
∴ ( ),
∴DF∥AE ( ).
9.如图,直角ABC的顶点B在直线b上,一边与直线a交于点A,且∠1 +∠2 = 90°.说明
直线 a∥b的理由.
【提优特训】
10.下列语句:①不相交、也不重合的两条直线叫平行线;②在同一平面内,两条直线的位置关系只有两种:相交和平行;③如果线段AB和线段CD不相交,那么直线AB和直线CD平行;④如果两条直线都和第三条直线平行,那么这两条直线平行;⑤过一点有且只有一条直线与已知直线平行.正确的个数是( )
A.1 B.2 C.3 D.4
11.如图,直线c与a、b分别相交于A、B两点,过点A作直线c的垂线交直线b于点C,
若∠1 = 55°,当∠2的度数为何值时a∥b ( )
A.55° B.45° C.35° D.25°
12.如图,直线a,b 被直线c、d所截.在下列条件中,能判定a∥ b 的是 ( )
A.∠3 = ∠4 B.∠1 = ∠2 C.∠2 = ∠3 D.∠3 + ∠5= 180°
13.如图,一个弯形管道ABCD的拐角∠ABC=110°,当∠BCD=( ),管道AB∥CD.
A.110° B.70° C.60° D.50°
14.(1)若∠1 = ∠2,根据 ,得 ∥ . (2)若∠2 + = ,
根据 ,得BD∥FG.
15.如图所示,若∠1+∠2=180°,∠4=∠3,AB与CD,EF与GH平行吗?
解:∵∠1+∠2=180°( ),∠1=∠4,
∴∠4+∠2=180°( )
∴AB∥ ( ),
∵∠4=∠3(已知),
∴∠3+∠ =180°( ),
∴EF∥GH( ).
16.请将下列证明过程补充完整:如图,已知点E在AB上,且CE平分∠ACD,∠1=∠2.试说明:
AB∥CD.
解:∵CE平分∠ACD,
∴∠ =∠ ( ),
∵∠1=∠2.(已知),
∴∠2=∠ ( ),
∴AB∥CD( ).
17.如图,台球桌上白球在A处,黑球在P处,用白球击打黑球必须通过二库将黑球送入中袋D中,路径为A→B→C→D,根据反射性质,∠1=∠2,∠3=∠4,试探究直线AB与CD是否平行?并说明理由.
18.已知:如图,AD ⊥ BC,EF ⊥ BC,∠1 = ∠2.求证:∠DGC = ∠BAC.
19.如图,已知点E在AB上,且CE,DE分别平分∠BCD和∠ADC,∠1+∠2=90°,试说明
AD∥BC.
20.如图,点B,A,F在一条直线上,∠1=∠2,∠FAC=∠B+∠C,且∠B=∠C,则AE∥BC吗?请说明理由.
【中考链接】
21.(2019?南京?2 分)结合图,用符号语言表达定理“同旁内角互补,两直线平行”的推理形式:
参考答案
1、A 2、B 3、D 4、C 5、平行(∥) 内错角相等,两直线平行. 10、B 11、C
12、D 13、B 14、(1)内错角相等,两直线平行,AB∥EF;(2) ∠3,180°,同旁内角互补,两直线平行A 15、北偏东55°
例题2的答案:证明:∵BE平分∠ABC(已知),
∴∠ABC =2∠1(角的平分线的定义).
∵CE平分∠BCD(已知),
∴∠BCD =2∠2(角的平分线的定义).
∴∠ABC +∠BCD =2∠1+2∠2=2(∠1+∠2)(等量代换).
∵∠1+∠2=90°(已知),
∴∠ABC+∠BCD=180°( 等式的性质).
∴AB∥CD(同旁内角互补,两直线平行).
6.如图,(1)如果∠1=∠D,那么 BE ∥ DF .根据是 同位角相等,两直线平行 .
(2)如果∠3=∠B,那么 AB ∥ CD ,根据是 内错角相等,两直线平行 .
(3)如果∠B+∠2= 180° ,那么AB∥CD,根据是 同旁内角互补,两直线平行 .
7.如图,点E在AB的延长线上,下列四个条件:①∠1=∠3;②∠2=∠4;③∠DAB=∠CBE;④∠D+∠BCD=180°.其中能判断AD∥CB的是 ② ③ ④ (填写正确的序号即可).
8.如图,已知CD⊥DA,DA⊥AB,∠1=∠4.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
证明:∵ CD⊥DA,DA⊥AB ,
∴∠CDA=90°,∠DAB=90° ( 垂直定义 ).
∴∠4+∠3=90°,∠2+∠1=90°.
又∵∠1=∠4,
∴∠2=∠3 ( 等式的性质 ),
∴DF∥AE ( 内错角相等,两直线平行 ).
9.如图,直角ABC的顶点B在直线b上,一边与直线a交于点A,且∠1 +∠2 = 90°.说明
直线 a∥b的理由.
解:方法一:∵ ∠1 + ∠2 = 90°,∠2 + ∠3 = 90°,
∴ ∠1 = ∠3.
∴a∥b(同位角相等,两直线平行).
方法二:同上得出 ∠1 = ∠3 .
∵ ∠1 = ∠4,
∴ ∠4 = ∠3 .
∴ a∥b(内错角相等,两直线平行) .
方法三:∵ ∠1 = ∠3,∠1 + ∠5 = 180°,
∴ ∠3 + ∠5 = 180° .
∴ a∥b(同旁内角互补,两直线平行).
15.如图所示,若∠1+∠2=180°,∠4=∠3,AB与CD,EF与GH平行吗?
解:∵∠1+∠2=180°( 已知 ),∠1=∠4,
∴∠4+∠2=180°(等量代换)
∴AB∥ CD (同旁内角互补,两条直线平行),
∵∠4=∠3(已知),
∴∠3+∠ 2 =180°(等量代换),
∴EF∥GH(__同旁内角互补,两直线平行__).
16.请将下列证明过程补充完整:如图,已知点E在AB上,且CE平分∠ACD,∠1=∠2.试说明:
AB∥CD.
解:∵CE平分∠ACD,
∴∠ 1 =∠ ECD ( 角平分线定义 ),
∵∠1=∠2.(已知),
∴∠2=∠ ECD ( 等量代换 ),
∴AB∥CD(内错角相等,两直线平行).
17.如图,台球桌上白球在A处,黑球在P处,用白球击打黑球必须通过二库将黑球送入中袋D中,路径为A→B→C→D,根据反射性质,∠1=∠2,∠3=∠4,试探究直线AB与CD是否平行?并说明理由.
解:AB∥CD,理由如下:
由题意得∠2+∠3=90°,
∵∠1=∠2,∠3=∠4,
∴∠1+∠2+∠3+∠4=90°+90°=180°,
∴∠ABC+∠BCD=360°(∠1+∠2+∠3+∠4)=180°.
∴AB∥CD(同旁内角互补,两直线平行).
18.已知:如图,AD ⊥ BC,EF ⊥ BC,∠1 = ∠2.求证:∠DGC = ∠BAC.
解:∵ AD⊥BC,FE⊥BC,
∴ ∠FEB = ∠ADB = 90°.
∴∠1+∠B=90°,∠2+∠CDG=90°.
∵ ∠1 = ∠2,
∴ ∠B = ∠CDG.
∵∠DGC=180°∠CDG∠C,∠BAC=180°∠B∠C
∴ ∠DGC = ∠BAC.
19.如图,已知点E在AB上,且CE,DE分别平分∠BCD和∠ADC,∠1+∠2=90°,试说明
AD∥BC.
证明:∵CE平分∠BCD,
∴∠BCD =2∠1.
∵DE平分∠ADC(已知),
∴∠ADC =2∠2.
∴∠ADC +∠BCD =2∠2+2∠1=2(∠1+∠2).
∵∠1+∠2=90°(已知),
∴∠ADC +∠BCD=180°.
∴AD∥BC.
20.如图,点B,A,F在一条直线上,∠1=∠2,∠FAC=∠B+∠C,且∠B=∠C,则AE∥BC吗?请说明理由.
解:AE∥BC.理由如下:
∵∠1=∠2,
∴∠1=∠2=∠FAC.
∵∠FAC=∠B+∠C,∠B=∠C,
∴∠B=∠C =∠FAC.
∴∠1=∠B.
∴AE∥BC(同位角相等,两直线平行).
【中考链接】
21.(2019?南京?2 分)结合图,用符号语言表达定理“同旁内角互补,两直线平行”的推理形式:
∵ ∠1+∠3=180° ,∴a∥b.
【分析】两条直线被第三条直线所截,如果同旁内角互补,
那么这两条直线平行.
【解答】解:∵∠1+∠3=180°,
∴a∥b(同旁内角互补,两直线平).
故答案为:∠1+∠3=180°.
1.3平行线的判定(2)
【知识清单】
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单地说,内错角相等,两直线平行.
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单地说,同旁内角互补,两直线平行.
【经典例题】
例题1.如图,下列说法中,正确的是( )
A.若∠3=∠6,则AB∥CD
B.若∠2=∠4,则AB∥CD
C.若∠DAB+∠ABC=180°,则AB∥CD
D.若∠1=∠5,则AB∥CD
【考点】平行线的判定.
【分析】根据平行线的判定,结合图形对选项一一分析,排除错误答案.
【解答】A、若∠3=∠6,不能判定AB∥CD,故选项错误;
B、若∠2=∠4,则AB∥CD,故选项错误;
C、若∠DAB+∠ABC=180°,则AB∥CD,故选项错误;
D、若∠1=∠5,则AB∥CD,故选项正确.
故选D.
【点评】正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,切记只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
例题2.完成下面的证明:
已知:如图.BE平分∠ABC,CE平分∠BCD,若∠1+∠2=90°.求证:AB∥CD.
证明:∵BE平分∠ABC( ),
∴∠ABC =2∠1( ).
∵CE平分∠BCD( ),
∴∠BCD =2 ( ).
∴∠ABC +∠BCD =2∠1+2∠2=2(∠1+∠2)( ).
∵∠1+∠2=90°( ),
∴∠ABC+∠BCD= ( ).
∴AB∥CD( ).
【考点】平行线的判定.?
【分析】首先根据角平分线的定义可得∠ABC=2∠1,∠BCD=2∠2,根据等量代换可
∠ABC +∠BCD =2∠1+2∠2=2(∠1+∠2),进而得到∠ABC+∠BCD =180°,然后再根据同旁内角互补两直线平行可得答案.
【解答】在参考答案里
【点评】此题主要考查了平行线的判定,关键是掌握角平分线定义和平行线的判定方法.
【夯实基础】
1.如图1-3-14,下列选项中,无法判断 l1∥l2的是( )
A.∠1=∠5 B.∠2=∠3 C.∠1=∠2 D.∠3+∠4=180°
2.如图所示,BE是∠MBN的平分线,点A在BM上,直线AC分别交BM、BE于点A、C,
下列条件:①∠1=∠2;②∠2=∠3;③∠1=∠MAC;④∠MBN+∠BAC=180°;
⑤∠MBN=∠MAC.其中能够使AC∥BN的条件个数为( )
A.2个 B.3个 C.4个 D.5个
3.已知,如图,要使得 AB∥CD,你认为不应该添加的一个条件是( )
A.∠1=∠A B.∠2=∠B C.∠A+∠ACD=180° D.∠B+∠BCE=180°
4.如图,已知∠1:∠2=3:7,要使AB∥CD,则∠1的度数为( )
A.27° B.36° C.54° D.126°
5.如图是一条公路的两个拐角,∠ABC与∠BCD均为146°,则公路 AB与CD的关系是
__________,这是因为_____________ ___________.
6.如图,(1)如果∠1=∠D,那么 ∥ .根据是 .
(2)如果∠3=∠B,那么 ∥ ,根据是 .
(3)如果∠B+∠2= ,那么AB∥CD,根据是 .
7.如图,点E在AB的延长线上,下列四个条件:①∠1=∠3;②∠2=∠4;③∠DAB=∠CBE;④∠D+∠BCD=180°.其中能判断AD∥CB的是 (填写正确的序号即可).
8.如图,已知CD⊥DA,DA⊥AB,∠1=∠4.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
证明:∵ ,
∴∠CDA=90°,∠DAB=90° ( ).
∴∠4+∠3=90°,∠2+∠1=90°.
又∵∠1=∠4,
∴ ( ),
∴DF∥AE ( ).
9.如图,直角ABC的顶点B在直线b上,一边与直线a交于点A,且∠1 +∠2 = 90°.说明
直线 a∥b的理由.
【提优特训】
10.下列语句:①不相交、也不重合的两条直线叫平行线;②在同一平面内,两条直线的位置关系只有两种:相交和平行;③如果线段AB和线段CD不相交,那么直线AB和直线CD平行;④如果两条直线都和第三条直线平行,那么这两条直线平行;⑤过一点有且只有一条直线与已知直线平行.正确的个数是( )
A.1 B.2 C.3 D.4
11.如图,直线c与a、b分别相交于A、B两点,过点A作直线c的垂线交直线b于点C,
若∠1 = 55°,当∠2的度数为何值时a∥b ( )
A.55° B.45° C.35° D.25°
12.如图,直线a,b 被直线c、d所截.在下列条件中,能判定a∥ b 的是 ( )
A.∠3 = ∠4 B.∠1 = ∠2 C.∠2 = ∠3 D.∠3 + ∠5= 180°
13.如图,一个弯形管道ABCD的拐角∠ABC=110°,当∠BCD=( ),管道AB∥CD.
A.110° B.70° C.60° D.50°
14.(1)若∠1 = ∠2,根据 ,得 ∥ . (2)若∠2 + = ,
根据 ,得BD∥FG.
15.如图所示,若∠1+∠2=180°,∠4=∠3,AB与CD,EF与GH平行吗?
解:∵∠1+∠2=180°( ),∠1=∠4,
∴∠4+∠2=180°( )
∴AB∥ ( ),
∵∠4=∠3(已知),
∴∠3+∠ =180°( ),
∴EF∥GH( ).
16.请将下列证明过程补充完整:如图,已知点E在AB上,且CE平分∠ACD,∠1=∠2.试说明:
AB∥CD.
解:∵CE平分∠ACD,
∴∠ =∠ ( ),
∵∠1=∠2.(已知),
∴∠2=∠ ( ),
∴AB∥CD( ).
17.如图,台球桌上白球在A处,黑球在P处,用白球击打黑球必须通过二库将黑球送入中袋D中,路径为A→B→C→D,根据反射性质,∠1=∠2,∠3=∠4,试探究直线AB与CD是否平行?并说明理由.
18.已知:如图,AD ⊥ BC,EF ⊥ BC,∠1 = ∠2.求证:∠DGC = ∠BAC.
19.如图,已知点E在AB上,且CE,DE分别平分∠BCD和∠ADC,∠1+∠2=90°,试说明
AD∥BC.
20.如图,点B,A,F在一条直线上,∠1=∠2,∠FAC=∠B+∠C,且∠B=∠C,则AE∥BC吗?请说明理由.
【中考链接】
21.(2019?南京?2 分)结合图,用符号语言表达定理“同旁内角互补,两直线平行”的推理形式:
参考答案
1、A 2、B 3、D 4、C 5、平行(∥) 内错角相等,两直线平行. 10、B 11、C
12、D 13、B 14、(1)内错角相等,两直线平行,AB∥EF;(2) ∠3,180°,同旁内角互补,两直线平行A 15、北偏东55°
例题2的答案:证明:∵BE平分∠ABC(已知),
∴∠ABC =2∠1(角的平分线的定义).
∵CE平分∠BCD(已知),
∴∠BCD =2∠2(角的平分线的定义).
∴∠ABC +∠BCD =2∠1+2∠2=2(∠1+∠2)(等量代换).
∵∠1+∠2=90°(已知),
∴∠ABC+∠BCD=180°( 等式的性质).
∴AB∥CD(同旁内角互补,两直线平行).
6.如图,(1)如果∠1=∠D,那么 BE ∥ DF .根据是 同位角相等,两直线平行 .
(2)如果∠3=∠B,那么 AB ∥ CD ,根据是 内错角相等,两直线平行 .
(3)如果∠B+∠2= 180° ,那么AB∥CD,根据是 同旁内角互补,两直线平行 .
7.如图,点E在AB的延长线上,下列四个条件:①∠1=∠3;②∠2=∠4;③∠DAB=∠CBE;④∠D+∠BCD=180°.其中能判断AD∥CB的是 ② ③ ④ (填写正确的序号即可).
8.如图,已知CD⊥DA,DA⊥AB,∠1=∠4.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
证明:∵ CD⊥DA,DA⊥AB ,
∴∠CDA=90°,∠DAB=90° ( 垂直定义 ).
∴∠4+∠3=90°,∠2+∠1=90°.
又∵∠1=∠4,
∴∠2=∠3 ( 等式的性质 ),
∴DF∥AE ( 内错角相等,两直线平行 ).
9.如图,直角ABC的顶点B在直线b上,一边与直线a交于点A,且∠1 +∠2 = 90°.说明
直线 a∥b的理由.
解:方法一:∵ ∠1 + ∠2 = 90°,∠2 + ∠3 = 90°,
∴ ∠1 = ∠3.
∴a∥b(同位角相等,两直线平行).
方法二:同上得出 ∠1 = ∠3 .
∵ ∠1 = ∠4,
∴ ∠4 = ∠3 .
∴ a∥b(内错角相等,两直线平行) .
方法三:∵ ∠1 = ∠3,∠1 + ∠5 = 180°,
∴ ∠3 + ∠5 = 180° .
∴ a∥b(同旁内角互补,两直线平行).
15.如图所示,若∠1+∠2=180°,∠4=∠3,AB与CD,EF与GH平行吗?
解:∵∠1+∠2=180°( 已知 ),∠1=∠4,
∴∠4+∠2=180°(等量代换)
∴AB∥ CD (同旁内角互补,两条直线平行),
∵∠4=∠3(已知),
∴∠3+∠ 2 =180°(等量代换),
∴EF∥GH(__同旁内角互补,两直线平行__).
16.请将下列证明过程补充完整:如图,已知点E在AB上,且CE平分∠ACD,∠1=∠2.试说明:
AB∥CD.
解:∵CE平分∠ACD,
∴∠ 1 =∠ ECD ( 角平分线定义 ),
∵∠1=∠2.(已知),
∴∠2=∠ ECD ( 等量代换 ),
∴AB∥CD(内错角相等,两直线平行).
17.如图,台球桌上白球在A处,黑球在P处,用白球击打黑球必须通过二库将黑球送入中袋D中,路径为A→B→C→D,根据反射性质,∠1=∠2,∠3=∠4,试探究直线AB与CD是否平行?并说明理由.
解:AB∥CD,理由如下:
由题意得∠2+∠3=90°,
∵∠1=∠2,∠3=∠4,
∴∠1+∠2+∠3+∠4=90°+90°=180°,
∴∠ABC+∠BCD=360°(∠1+∠2+∠3+∠4)=180°.
∴AB∥CD(同旁内角互补,两直线平行).
18.已知:如图,AD ⊥ BC,EF ⊥ BC,∠1 = ∠2.求证:∠DGC = ∠BAC.
解:∵ AD⊥BC,FE⊥BC,
∴ ∠FEB = ∠ADB = 90°.
∴∠1+∠B=90°,∠2+∠CDG=90°.
∵ ∠1 = ∠2,
∴ ∠B = ∠CDG.
∵∠DGC=180°∠CDG∠C,∠BAC=180°∠B∠C
∴ ∠DGC = ∠BAC.
19.如图,已知点E在AB上,且CE,DE分别平分∠BCD和∠ADC,∠1+∠2=90°,试说明
AD∥BC.
证明:∵CE平分∠BCD,
∴∠BCD =2∠1.
∵DE平分∠ADC(已知),
∴∠ADC =2∠2.
∴∠ADC +∠BCD =2∠2+2∠1=2(∠1+∠2).
∵∠1+∠2=90°(已知),
∴∠ADC +∠BCD=180°.
∴AD∥BC.
20.如图,点B,A,F在一条直线上,∠1=∠2,∠FAC=∠B+∠C,且∠B=∠C,则AE∥BC吗?请说明理由.
解:AE∥BC.理由如下:
∵∠1=∠2,
∴∠1=∠2=∠FAC.
∵∠FAC=∠B+∠C,∠B=∠C,
∴∠B=∠C =∠FAC.
∴∠1=∠B.
∴AE∥BC(同位角相等,两直线平行).
【中考链接】
21.(2019?南京?2 分)结合图,用符号语言表达定理“同旁内角互补,两直线平行”的推理形式:
∵ ∠1+∠3=180° ,∴a∥b.
【分析】两条直线被第三条直线所截,如果同旁内角互补,
那么这两条直线平行.
【解答】解:∵∠1+∠3=180°,
∴a∥b(同旁内角互补,两直线平).
故答案为:∠1+∠3=180°.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
