1.4.1 平行线的性质(知识清单+经典例题+夯实基础+提优特训+中考链接)
文档属性
| 名称 | 1.4.1 平行线的性质(知识清单+经典例题+夯实基础+提优特训+中考链接) |  | |
| 格式 | zip | ||
| 文件大小 | 390.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-25 17:52:15 | ||
图片预览


文档简介
浙江版2019-2020学年度下学期七年级数学下册第1章平行线
1.4平行线的性质(1)
【知识清单】
两条平行线被第三条直线所截,同位角相等.
简单地说,两直线平行,同位角相等.
【经典例题】
例题1.如图所示,已知 AB∥CD,EF 平分∠CEG,∠1=62°,则 ∠2 的度数为
A.40° B.46° C.48° D.56°
【考点】?平行线的性质.
【分析】根据平行线的性质,结合图形对选项一一分析,排除错误答案.
【解答】∵EF平分∠CEG,
∴∠CEG =2∠CEF.
∵∠1与∠3是对顶角,∠1=62°,
∴∠1=∠3=62°,.
又∵AB∥CD,
∴∠3=∠CEF,
∴∠CEG =2∠CEF=2∠3=124°.
∵∠CEG+∠GED=180°,
∴∠GED=180°∠CEG=56°.
∵AB∥CD,
∴∠2=∠GED=56°.
故选项为D.
【点评】此题主要考查了平行线的性质两直线平行,同位角相等.正确地将已知角转化为同位角是解决问题的关键.
例题2.若一个角的两边与另一个角的两边分别平行,则这两个角的关系 .
【考点】平行线的性质.
【分析】根据平行线的性质:两直线平行同位角相等、邻补角定义以及作图求解即可.
【解答】?这两个角相等或互补相等或互补.理由如下:
如图(1),∵BC∥,
∴∠1=∠,
∵AB∥,
∴∠B=∠1=∠.
如图(2),∵BC∥,
∴∠1=∠,
∵AB∥,
∴∠B=∠2.
∵∠1+∠2=180°,
∴∠B+∠=180°.
即这两个角相等或互补.
【点评】本题考查了平行线的性质,熟记性质并正确地作出图形是解题的关键,注意此题有两种情况,不要遗漏.
【夯实基础】
1.下列图形中∠1与∠2不相等的是( )
2.如图,直线AB∥CD,AF交CD于点E,∠CEC=145°,则∠A等于( )
A.25° B.35° C.45° D.55°
3.两条平行线被第三条直线所截,则一对同位角的角平分线( )
A.相交 B.垂直 C.平行 D.不能确定
4.如图,AB∥CD,EF∥GH,∠1与∠2的关系为( )
A.相等 B.互补 C.互余 D.不能确定
5.如图,已知a∥b, c⊥a,判断c与b的位置关系为 .
6.如图,AB∥CD,EF分别交AB,CD于G,H,且∠1=3∠2,求∠2的度数.
解:∵AB∥CD,∴∠2=∠ HGB ( ),
∵∠1=3∠2( ),
∠1+∠BGH=180°( ),
∴3∠2+∠2=180°( ),
解得∠2=45°.
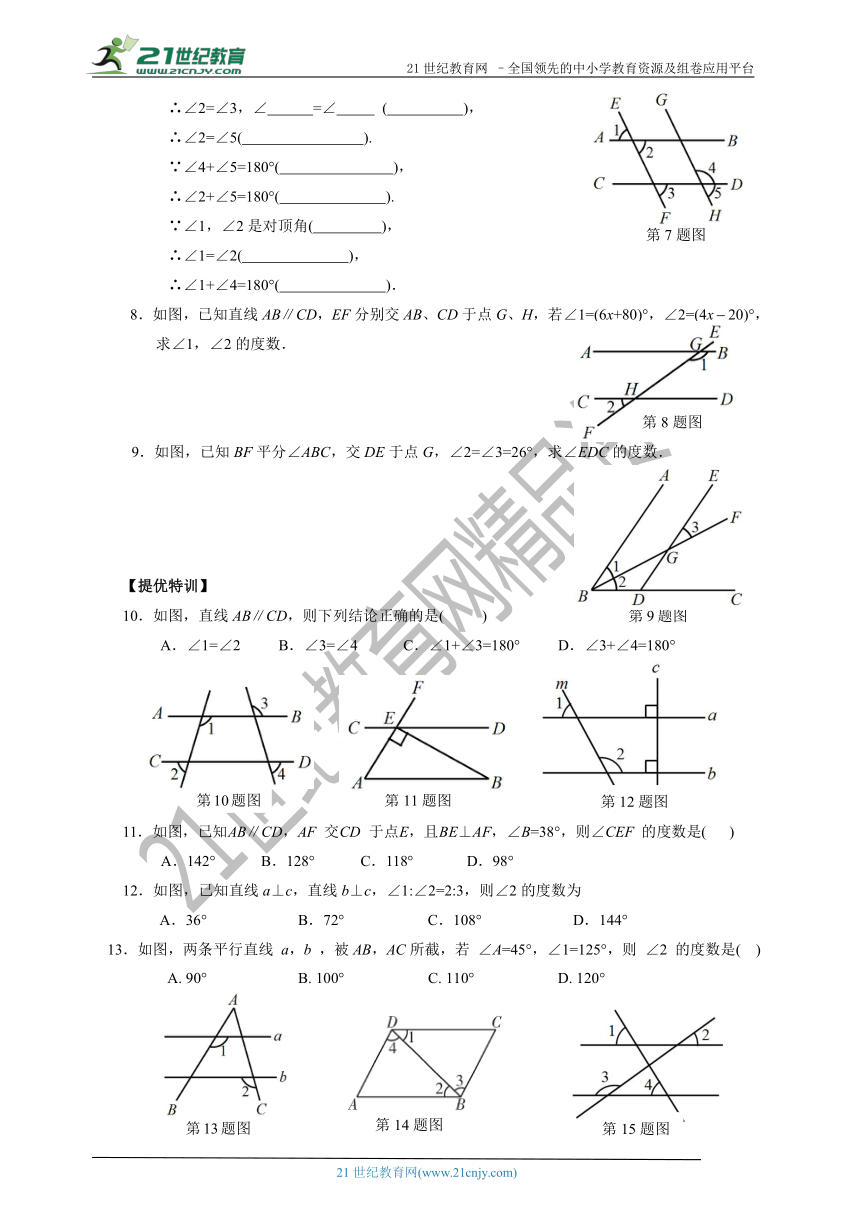
7.如图所示,AB∥CD,EF∥GH,试探究∠1与∠4的关系,并说明理由.
解:∠1+∠4=180°. 理由如下:
∵AB∥CD,EF∥GH,( ),
∴∠2=∠3,∠ =∠ ( ),
∴∠2=∠5( ).
∵∠4+∠5=180°( ),
∴∠2+∠5=180°( ).
∵∠1,∠2是对顶角( ),
∴∠1=∠2( ),
∴∠1+∠4=180°( ).
8.如图,已知直线AB∥CD,EF分别交AB、CD于点G、H,若∠1=(6x+80)°,∠2=(4x20)°,求∠1,∠2的度数.
9.如图,已知BF平分∠ABC,交DE于点G,∠2=∠3=26°,求∠EDC的度数.
【提优特训】
10.如图,直线AB∥CD,则下列结论正确的是( )
A.∠1=∠2 B.∠3=∠4 C.∠1+∠3=180° D.∠3+∠4=180°
11.如图,已知 AB∥CD,AF 交 CD 于点 E,且 BE⊥AF,∠B=38°,则∠CEF 的度数是( )
A.142° B.128° C.118° D.98°
12.如图,已知直线a⊥c,直线b⊥c,∠1:∠2=2:3,则∠2的度数为
A.36° B.72° C.108° D.144°
13.如图,两条平行直线 a,b ,被AB,AC所截,若 ∠A=45°,∠1=125°,则 ∠2 的度数是( )
A. 90° B. 100° C. 110° D. 120°
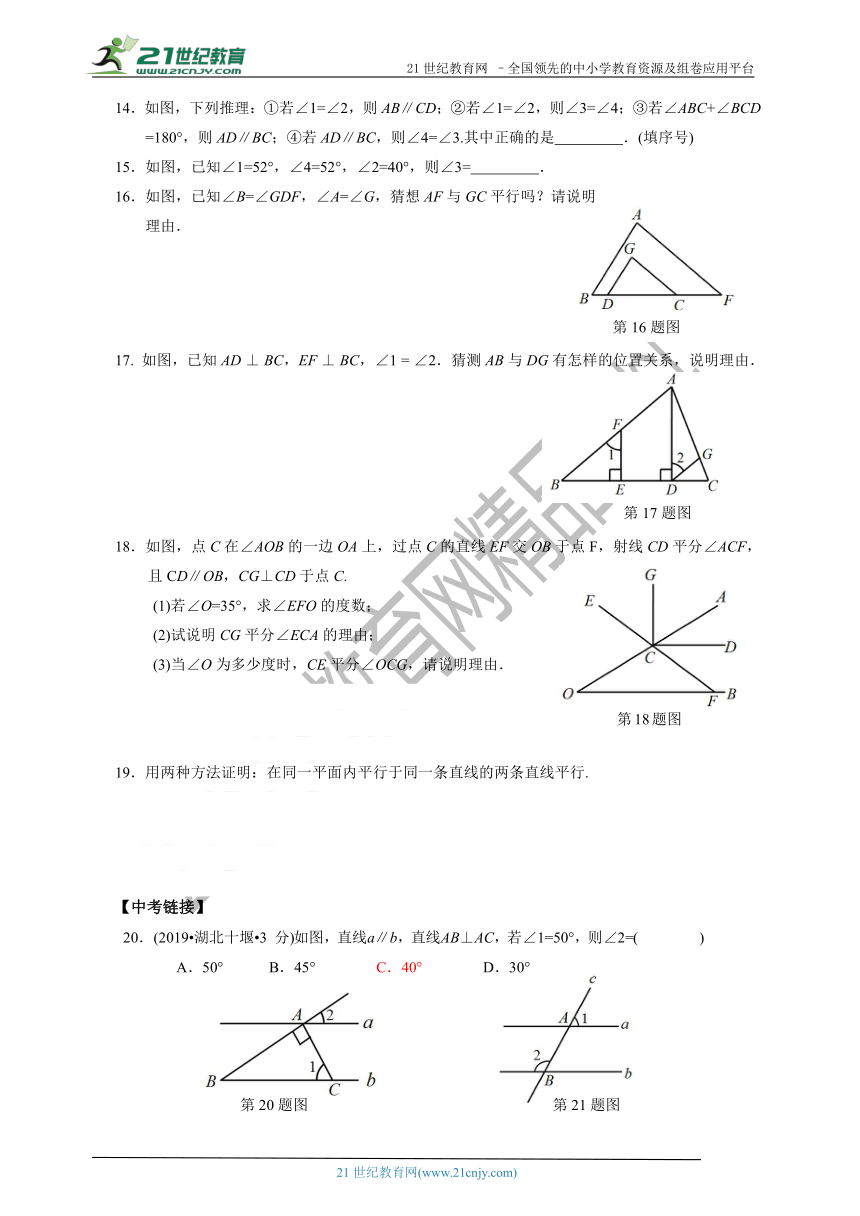
14.如图,下列推理:①若∠1=∠2,则AB∥CD;②若∠1=∠2,则∠3=∠4;③若∠ABC+∠BCD
=180°,则AD∥BC;④若AD∥BC,则∠4=∠3.其中正确的是 .(填序号)
15.如图,已知∠1=52°,∠4=52°,∠2=40°,则∠3= .
16.如图,已知∠B=∠GDF,∠A=∠G,猜想AF与GC平行吗?请说明
理由.
17. 如图,已知AD ⊥ BC,EF ⊥ BC,∠1 = ∠2.猜测AB与DG有怎样的位置关系,说明理由.
18.如图,点C在∠AOB的一边OA上,过点C的直线EF交OB于点F,射线CD平分∠ACF,且CD∥OB,CG⊥CD于点C.
(1)若∠O=35°,求∠EFO的度数;
(2)试说明CG平分∠ECA的理由;
(3)当∠O为多少度时,CE平分∠OCG,请说明理由.
19.用两种方法证明:在同一平面内平行于同一条直线的两条直线平行.
【中考链接】
20.(2019?湖北十堰?3 分)如图,直线 a∥b,直线 AB⊥AC,若∠1=50°,则∠2=( )
A.50° B.45° C.40° D.30°
21.(2019?江苏苏州?3 分)如图,已知直线 a//b ,直线 c与直线 a,b 分别交于点 A,B.
若(1 ( 54° ,则 (2 ( ( )
A.126° B.134° C.136° D.144°
22.(2019?湖南长沙?3 分)如图,平行线 AB,CD 被直线 AE 所截,∠1=80°,则∠2 的度数
是( )
A.80° B.90° C.100° D.110°
23.(2019?湖南湘西州?4 分)如图,直线 a∥b,∠1=50°,∠2=40°,则∠3 的度数为( )
A.40° B.90° C.50° D.100°
参考答案
1、B 2、B 3、C 4、A 5、b⊥c. 10、D 11、B 12、C 13、B 14、①④
15、140° 20、C 21、A 22、C 23、B
6.如图,AB∥CD,EF分别交AB,CD于G,H,且∠1=3∠2,求∠2的度数.
解:∵AB∥CD,∴∠2=∠ HGB (两直线平行,同位角相等 ),
∵∠1=3∠2( 已知 ),
∠1+∠BGH=180°( 邻补角定义 ),
∴3∠2+∠2=180°( 等量代换 ),
解得∠2=45°.
7.如图所示,AB∥CD,EF∥GH,试探究∠1与∠4的关系,并说明理由.
解:∠1+∠4=180°. 理由如下:
∵AB∥CD,EF∥GH,( 已知 ),
∴∠2=∠3,∠ 3 =∠ 5 (两直线平行,同位角相等),
∴∠2=∠5( 等量代换 ).
∵∠4+∠5=180°( 邻补角定义 ),
∴∠2+∠5=180°( 等量代换 ).
∵∠1,∠2是对顶角( 已知 ),
∴∠1=∠2( 对顶角相等 ),
∴∠1+∠4=180°(等量代换).
8.如图,已知直线AB∥CD,EF分别交AB、CD于点G、H,若∠1=(6x+80)°,∠2=(4x20)°,求∠1,∠2的度数.
解:∵AB∥CD,
∴∠1=∠DHF,(两直线平行,同位角相等)
∵∠DHF +∠2=180°,
∴∠DHF =180°-∠2=180°(4x20)°.
∴6x+80=180(4x20),
即10x=120,解得x=12.
∴∠1=(6x+80)°=152°,∠2=(4x20)°=28°.
9.如图,已知BF平分∠ABC,交DE于点G,∠2=∠3=26°,求∠EDC的度数.
解:∵BF平分∠ABC,
∴∠1=∠2.
∵∠2=∠3=26°,
∴∠1=∠3=26°.
∴AB∥DE
∴∠EDC=∠ABC=∠1+∠2=52°.
16.如图,已知∠B=∠GDF,∠A=∠G,猜想AF与GC平行吗?请说明
理由.
解:AF∥GC.理由如下:
延长DG交AF于点E,
∵∠B=∠GDF,
∴AB∥GD,
∴∠A=∠DEF.
∵∠A=∠G,
∴∠DEF =∠A,
∴AF∥GC.
17. 如图,已知AD ⊥ BC,EF ⊥ BC,∠1 = ∠2.猜测AB与DG有怎样的位置关系,说明理由.
解:AB∥DG,理由如下:
∵ AD⊥BC,FE⊥BC,
∴ ∠FEB = ∠ADB = 90°.
∴∠1+∠B=90°,∠2+∠CDG=90°.
∵ ∠1 = ∠2,
∴ ∠B = ∠CDG.
∵∠DGC=180°∠CDG∠C,∠BAC=180°∠B∠C
∴ ∠DGC = ∠BAC.
∴AB∥DG.
18.如图,点C在∠AOB的一边OA上,过点C的直线EF交OB于点F,射线CD平分∠ACF,且CD∥OB,CG⊥CD于点C.
(1)若∠O=35°,求∠EFO的度数;
(2)试说明CG平分∠ECA的理由;
(3)当∠O为多少度时,CE平分∠OCG,请说明理由.
解:(1)∵CD∥OB,
∴∠O=∠ACD.
∵∠O=35°,
∴∠ACD=∠O=35°.
∵CD平分∠ACF,
∴∠ACD=∠FCD=35°.
∴∠ACF=∠ACD+∠FCD=70°,
∵∠ACF+∠OCF=180°,
∴∠OCF=180°∠ACF=110°.
∵∠O+∠OCF+∠OFC=180°.
∴∠OFC=180°∠O-∠OCF=35°.
(2)∵CG⊥CD,∴∠DCG=90°,
∴∠ACG+∠ACD=90°,∠GCE+∠FCD=90°,
∵∠ACD=∠FCD,
∴∠ACG=∠ECG,即CG平分∠ECA;
(3)当∠O=30°时,CE平分∠OCG.理由如下:
当∠O=30°时,∵CD∥OB,
∴∠ACD=∠FCD=∠O=30°,
∴∠ACF=60°,∠ACG=∠ECG=60°.
又∵∠OCE与∠ACF是对顶角,
∴∠OCE=∠ACF =60°,
∴∠ECO=∠ECD,即CE平分∠OCG.
19.用两种方法证明:在同一平面内平行于同一条直线的两条直线平行
已知:a∥c,b∥c.求证:a∥b
证明:方法一,如图(1):
?????? ∵a∥c,
?????? ∴∠1=∠3(两直线平行,同位角相等).
?????? ? ∵b∥c,
?????? ∴∠3=∠2(两直线平行,同位角相等).
????? ? ∴∠1=∠2
?????? ? ?∴a∥b??(同位角相等,两直线平行).
方法二,如图(2): 假设a、b不平行,
则a、b交于一点P.
又∵a∥c,b∥c,
∴过P有a、b两条直线平行于c,这与经过直线外一点有且只有一条直线平行于已知直线
矛盾.
∴假设不成立.
∴b∥c.
1.4平行线的性质(1)
【知识清单】
两条平行线被第三条直线所截,同位角相等.
简单地说,两直线平行,同位角相等.
【经典例题】
例题1.如图所示,已知 AB∥CD,EF 平分∠CEG,∠1=62°,则 ∠2 的度数为
A.40° B.46° C.48° D.56°
【考点】?平行线的性质.
【分析】根据平行线的性质,结合图形对选项一一分析,排除错误答案.
【解答】∵EF平分∠CEG,
∴∠CEG =2∠CEF.
∵∠1与∠3是对顶角,∠1=62°,
∴∠1=∠3=62°,.
又∵AB∥CD,
∴∠3=∠CEF,
∴∠CEG =2∠CEF=2∠3=124°.
∵∠CEG+∠GED=180°,
∴∠GED=180°∠CEG=56°.
∵AB∥CD,
∴∠2=∠GED=56°.
故选项为D.
【点评】此题主要考查了平行线的性质两直线平行,同位角相等.正确地将已知角转化为同位角是解决问题的关键.
例题2.若一个角的两边与另一个角的两边分别平行,则这两个角的关系 .
【考点】平行线的性质.
【分析】根据平行线的性质:两直线平行同位角相等、邻补角定义以及作图求解即可.
【解答】?这两个角相等或互补相等或互补.理由如下:
如图(1),∵BC∥,
∴∠1=∠,
∵AB∥,
∴∠B=∠1=∠.
如图(2),∵BC∥,
∴∠1=∠,
∵AB∥,
∴∠B=∠2.
∵∠1+∠2=180°,
∴∠B+∠=180°.
即这两个角相等或互补.
【点评】本题考查了平行线的性质,熟记性质并正确地作出图形是解题的关键,注意此题有两种情况,不要遗漏.
【夯实基础】
1.下列图形中∠1与∠2不相等的是( )
2.如图,直线AB∥CD,AF交CD于点E,∠CEC=145°,则∠A等于( )
A.25° B.35° C.45° D.55°
3.两条平行线被第三条直线所截,则一对同位角的角平分线( )
A.相交 B.垂直 C.平行 D.不能确定
4.如图,AB∥CD,EF∥GH,∠1与∠2的关系为( )
A.相等 B.互补 C.互余 D.不能确定
5.如图,已知a∥b, c⊥a,判断c与b的位置关系为 .
6.如图,AB∥CD,EF分别交AB,CD于G,H,且∠1=3∠2,求∠2的度数.
解:∵AB∥CD,∴∠2=∠ HGB ( ),
∵∠1=3∠2( ),
∠1+∠BGH=180°( ),
∴3∠2+∠2=180°( ),
解得∠2=45°.
7.如图所示,AB∥CD,EF∥GH,试探究∠1与∠4的关系,并说明理由.
解:∠1+∠4=180°. 理由如下:
∵AB∥CD,EF∥GH,( ),
∴∠2=∠3,∠ =∠ ( ),
∴∠2=∠5( ).
∵∠4+∠5=180°( ),
∴∠2+∠5=180°( ).
∵∠1,∠2是对顶角( ),
∴∠1=∠2( ),
∴∠1+∠4=180°( ).
8.如图,已知直线AB∥CD,EF分别交AB、CD于点G、H,若∠1=(6x+80)°,∠2=(4x20)°,求∠1,∠2的度数.
9.如图,已知BF平分∠ABC,交DE于点G,∠2=∠3=26°,求∠EDC的度数.
【提优特训】
10.如图,直线AB∥CD,则下列结论正确的是( )
A.∠1=∠2 B.∠3=∠4 C.∠1+∠3=180° D.∠3+∠4=180°
11.如图,已知 AB∥CD,AF 交 CD 于点 E,且 BE⊥AF,∠B=38°,则∠CEF 的度数是( )
A.142° B.128° C.118° D.98°
12.如图,已知直线a⊥c,直线b⊥c,∠1:∠2=2:3,则∠2的度数为
A.36° B.72° C.108° D.144°
13.如图,两条平行直线 a,b ,被AB,AC所截,若 ∠A=45°,∠1=125°,则 ∠2 的度数是( )
A. 90° B. 100° C. 110° D. 120°
14.如图,下列推理:①若∠1=∠2,则AB∥CD;②若∠1=∠2,则∠3=∠4;③若∠ABC+∠BCD
=180°,则AD∥BC;④若AD∥BC,则∠4=∠3.其中正确的是 .(填序号)
15.如图,已知∠1=52°,∠4=52°,∠2=40°,则∠3= .
16.如图,已知∠B=∠GDF,∠A=∠G,猜想AF与GC平行吗?请说明
理由.
17. 如图,已知AD ⊥ BC,EF ⊥ BC,∠1 = ∠2.猜测AB与DG有怎样的位置关系,说明理由.
18.如图,点C在∠AOB的一边OA上,过点C的直线EF交OB于点F,射线CD平分∠ACF,且CD∥OB,CG⊥CD于点C.
(1)若∠O=35°,求∠EFO的度数;
(2)试说明CG平分∠ECA的理由;
(3)当∠O为多少度时,CE平分∠OCG,请说明理由.
19.用两种方法证明:在同一平面内平行于同一条直线的两条直线平行.
【中考链接】
20.(2019?湖北十堰?3 分)如图,直线 a∥b,直线 AB⊥AC,若∠1=50°,则∠2=( )
A.50° B.45° C.40° D.30°
21.(2019?江苏苏州?3 分)如图,已知直线 a//b ,直线 c与直线 a,b 分别交于点 A,B.
若(1 ( 54° ,则 (2 ( ( )
A.126° B.134° C.136° D.144°
22.(2019?湖南长沙?3 分)如图,平行线 AB,CD 被直线 AE 所截,∠1=80°,则∠2 的度数
是( )
A.80° B.90° C.100° D.110°
23.(2019?湖南湘西州?4 分)如图,直线 a∥b,∠1=50°,∠2=40°,则∠3 的度数为( )
A.40° B.90° C.50° D.100°
参考答案
1、B 2、B 3、C 4、A 5、b⊥c. 10、D 11、B 12、C 13、B 14、①④
15、140° 20、C 21、A 22、C 23、B
6.如图,AB∥CD,EF分别交AB,CD于G,H,且∠1=3∠2,求∠2的度数.
解:∵AB∥CD,∴∠2=∠ HGB (两直线平行,同位角相等 ),
∵∠1=3∠2( 已知 ),
∠1+∠BGH=180°( 邻补角定义 ),
∴3∠2+∠2=180°( 等量代换 ),
解得∠2=45°.
7.如图所示,AB∥CD,EF∥GH,试探究∠1与∠4的关系,并说明理由.
解:∠1+∠4=180°. 理由如下:
∵AB∥CD,EF∥GH,( 已知 ),
∴∠2=∠3,∠ 3 =∠ 5 (两直线平行,同位角相等),
∴∠2=∠5( 等量代换 ).
∵∠4+∠5=180°( 邻补角定义 ),
∴∠2+∠5=180°( 等量代换 ).
∵∠1,∠2是对顶角( 已知 ),
∴∠1=∠2( 对顶角相等 ),
∴∠1+∠4=180°(等量代换).
8.如图,已知直线AB∥CD,EF分别交AB、CD于点G、H,若∠1=(6x+80)°,∠2=(4x20)°,求∠1,∠2的度数.
解:∵AB∥CD,
∴∠1=∠DHF,(两直线平行,同位角相等)
∵∠DHF +∠2=180°,
∴∠DHF =180°-∠2=180°(4x20)°.
∴6x+80=180(4x20),
即10x=120,解得x=12.
∴∠1=(6x+80)°=152°,∠2=(4x20)°=28°.
9.如图,已知BF平分∠ABC,交DE于点G,∠2=∠3=26°,求∠EDC的度数.
解:∵BF平分∠ABC,
∴∠1=∠2.
∵∠2=∠3=26°,
∴∠1=∠3=26°.
∴AB∥DE
∴∠EDC=∠ABC=∠1+∠2=52°.
16.如图,已知∠B=∠GDF,∠A=∠G,猜想AF与GC平行吗?请说明
理由.
解:AF∥GC.理由如下:
延长DG交AF于点E,
∵∠B=∠GDF,
∴AB∥GD,
∴∠A=∠DEF.
∵∠A=∠G,
∴∠DEF =∠A,
∴AF∥GC.
17. 如图,已知AD ⊥ BC,EF ⊥ BC,∠1 = ∠2.猜测AB与DG有怎样的位置关系,说明理由.
解:AB∥DG,理由如下:
∵ AD⊥BC,FE⊥BC,
∴ ∠FEB = ∠ADB = 90°.
∴∠1+∠B=90°,∠2+∠CDG=90°.
∵ ∠1 = ∠2,
∴ ∠B = ∠CDG.
∵∠DGC=180°∠CDG∠C,∠BAC=180°∠B∠C
∴ ∠DGC = ∠BAC.
∴AB∥DG.
18.如图,点C在∠AOB的一边OA上,过点C的直线EF交OB于点F,射线CD平分∠ACF,且CD∥OB,CG⊥CD于点C.
(1)若∠O=35°,求∠EFO的度数;
(2)试说明CG平分∠ECA的理由;
(3)当∠O为多少度时,CE平分∠OCG,请说明理由.
解:(1)∵CD∥OB,
∴∠O=∠ACD.
∵∠O=35°,
∴∠ACD=∠O=35°.
∵CD平分∠ACF,
∴∠ACD=∠FCD=35°.
∴∠ACF=∠ACD+∠FCD=70°,
∵∠ACF+∠OCF=180°,
∴∠OCF=180°∠ACF=110°.
∵∠O+∠OCF+∠OFC=180°.
∴∠OFC=180°∠O-∠OCF=35°.
(2)∵CG⊥CD,∴∠DCG=90°,
∴∠ACG+∠ACD=90°,∠GCE+∠FCD=90°,
∵∠ACD=∠FCD,
∴∠ACG=∠ECG,即CG平分∠ECA;
(3)当∠O=30°时,CE平分∠OCG.理由如下:
当∠O=30°时,∵CD∥OB,
∴∠ACD=∠FCD=∠O=30°,
∴∠ACF=60°,∠ACG=∠ECG=60°.
又∵∠OCE与∠ACF是对顶角,
∴∠OCE=∠ACF =60°,
∴∠ECO=∠ECD,即CE平分∠OCG.
19.用两种方法证明:在同一平面内平行于同一条直线的两条直线平行
已知:a∥c,b∥c.求证:a∥b
证明:方法一,如图(1):
?????? ∵a∥c,
?????? ∴∠1=∠3(两直线平行,同位角相等).
?????? ? ∵b∥c,
?????? ∴∠3=∠2(两直线平行,同位角相等).
????? ? ∴∠1=∠2
?????? ? ?∴a∥b??(同位角相等,两直线平行).
方法二,如图(2): 假设a、b不平行,
则a、b交于一点P.
又∵a∥c,b∥c,
∴过P有a、b两条直线平行于c,这与经过直线外一点有且只有一条直线平行于已知直线
矛盾.
∴假设不成立.
∴b∥c.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
