浙教版七年级数学下册1.2平行线与三线八角双课时练(附答案)
文档属性
| 名称 | 浙教版七年级数学下册1.2平行线与三线八角双课时练(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-29 12:52:33 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
平行线与三线八角双课时练
一、单选题
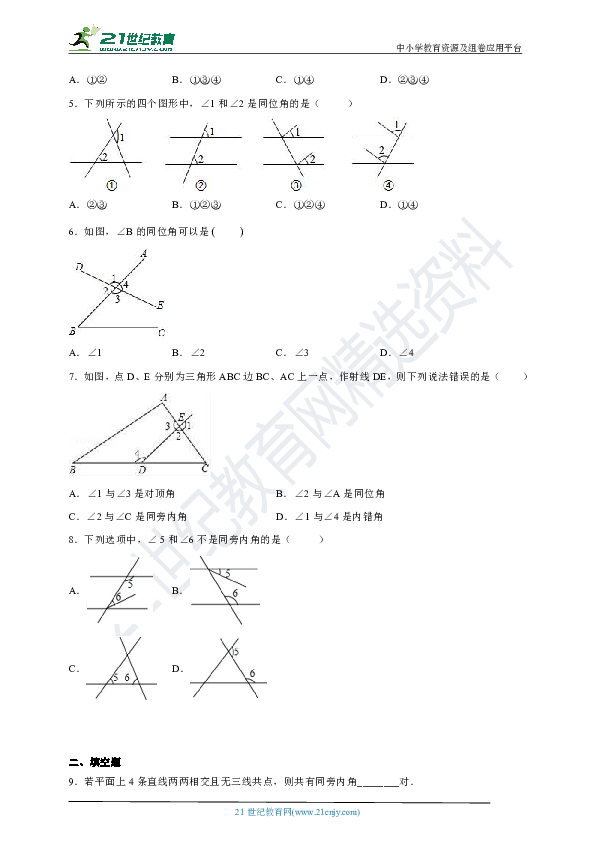
1.如图,直线AB,CD相交于点O,EO⊥AB,垂直为点O,∠BOD=50°,则∠COE=( )
A.30° B.140° C.50° D.60°
2.如图,给出下列说法:①∠B和∠1是同位角;②∠1和∠3是对顶角;③ ∠2和∠4是内错角;④ ∠A和∠BCD是同旁内角. 其中说法正确的有( )
A.0个 B.1个 C.2个 D.3个
3.下列选项中∠1与∠2不是同位角的是( )
A. B.
C. D.
4.下列命题,其中为真命题的是( )
①经过直线外一点,有且只有一条直线与已知直线平行;
②同位角相等;
③过一点有且只有一条直线与已知直线垂直;
④对顶角相等.
A.①② B.①③④ C.①④ D.②③④
5.下列所示的四个图形中,∠1和∠2是同位角的是( )
A.②③ B.①②③ C.①②④ D.①④
6.如图,∠B的同位角可以是
A.∠1 B.∠2 C.∠3 D.∠4
7.如图,点D、E分别为三角形ABC边BC、AC上一点,作射线DE,则下列说法错误的是( )
A.∠1与∠3是对顶角 B.∠2与∠A是同位角
C.∠2与∠C是同旁内角 D.∠1与∠4是内错角
8.下列选项中,∠ 5和∠6不是同旁内角的是( )
A. B.
C. D.
二、填空题
9.若平面上4条直线两两相交且无三线共点,则共有同旁内角________对.
10.探究题:
(1)如图1,两条水平的直线被一条竖直的直线所截,同位角有____对,内错角有_____对,同旁内角有_____对;
(2)如图2,三条水平的直线被一条竖直的直线所截,同位角有____对,内错角有___对,同旁内角有___对;
(3)根据以上探究的结果,n(n为大于1的整数)条水平直线被一条竖直直线所截,同位角有______对,内错角有_______对,同旁内角有______对.(用含n的式子表示)
11.若平面上四条直线两两相交,且无三线共点,则一共有___________对内错角.
三、解答题
12.如图,直线AB,CD相交于点O,OE平分,,
图中的余角是______把符合条件的角都填出来;
如果,那么根据______可得______度;
如果,求和的度数.
13.如图,直线AB,CD相交于点O,OE⊥CD于点O,OD平分∠BOF,∠BOE=50,
求∠AOC,∠AOF,∠EOF的度数.
14.如图所示,如果内错角∠1与∠5相等,那么与∠1相等的角还有吗?与∠1互补的角有吗?如果有,请写出来,并说明你的理由.
15.如图,BE是AB的延长线,指出下面各组中的两个角是由哪两条直线被哪一条直线所截形成的?它们是什么角?
(1)∠A和∠D;
(2)∠A和∠CBA;
(3)∠C和∠CBE.
16.如图,已知直线a,b被直线c,d所截,直线a,c,d相交于点O,按要求完成下列各小题.
(1)在图中的∠1~∠9这9个角中,同位角共有多少对?请你全部写出来;
(2)∠4和∠5是什么位置关系的角?∠6和∠8之间的位置关系与∠4和∠5的相同吗?
17.如图,∠1与∠2,∠3与∠4,分别是什么关系?分别是哪两条直线被哪一条直线所截形成的?
18.如图,BCD是一条直线,∠1=∠B,∠2=∠A,指出∠1的同位角,∠2的内错角,并求出∠A+∠B+∠ACB的度数.
19.如图,点在网格的格点上,每小方格是边长为 个单位长度的正方形.请按要求画图,并回答问题:
延长线段到点,使;
过点 画直线的垂线,垂足为;并直接写出点 到直线的距离;
过点画交 于点;
请写出图中的所有同位角.
参考答案
1.B【解析】EO⊥AB,
故选B.
2.B【解析】:由图可知,
∠B和∠1是同旁内角,故①、②错误;
∠2和∠4是内错角,故③正确;
∠A和∠BCD不是同旁内角,故④错误;
∴正确的只有1个;故选:B.
3.C【解析】A、B、D中∠1和∠2是同位角;C、∠1和∠2不满足两条直线被第三条直线所截形成的角,所以不是同位角;故选:C.
4.C【解析】经过直线外一点,有且只有一条直线与已知直线平行,所以①正确;
两直线平行,同位角相等,缺少条件,所以②错误;
在同一平面内,过一点有且只有一条直线与已知直线垂直,所以③错误;
对顶角相等,所以④正确.
5.C【解析】图①、②、④中,∠1与∠2在截线的同侧,并且在被截线的同一方,是同位角;
图③中,∠1与∠2的两条边都不在同一条直线上,不是同位角.
故选C.
6.D【解析】∠B的同位角可以是:∠4.
故选D.
7.D【解析】A、∠1与∠3是对顶角,说法正确;
B、∠2与∠A是同位角,说法正确;
C、∠2与∠C是同旁内角,说法正确;
D、∠2与∠4是内错角,说法错误.
故选:D.
8.B【解析】
A. ∠5和∠6是同旁内角,不合题意,故此选项错误.
B.∠5和∠6不是同旁内角,符合题意,故此选项正确
C.∠5和∠6是同旁内角,不合题意,故此选项错误
D.∠5和∠6是同旁内角,不合题意,故此选项错误
9.24
【解析】如图所示
观测点A和点B,同旁内角有2对;A和C有2对;A和D,没有同旁内角;A和E有2对;A和F有2对.B和C有2对;B和D有2对;B和E有2对;B和F没有同旁内角.C和D有2对,C和E没有同旁内角,C和F有2对.D和E有2对;D和F有2对.E和F有2对.共有2×12=24对.
故答案是:24.
10.(1)4,2,2;(2)12,6,6;(3)2n(n-1),n(n-1),n(n-1)
【解析】
(1)如图1,两条水平的直线被一条竖直的直线所截,同位角有4对,内错角有 2对,同旁内角有 2对.
(2)如图2,三条水平的直线被一条竖直的直线所截,同位角有 12对,内错角有 6对,同旁内角有 6对.
(3)根据以上探究的结果,n(n为大于1的整数)条水平直线被一条竖直直线所截,同位角有2n(n-1)对,内错角有 n(n-1)对,同旁内角有n(n-1)对,
11.24
【解析】∵平面上4条直线两两相交且无三线共点,
∴共有3×4=12条线段,
又∵每条线段两侧共有2对内错角,
∴共有内错角 12×2=24对,
故答案为:24.
12.(1)∠BOC、∠AOD(2)对顶角相等,160(3)26°
【解析】(1)图中∠AOF的余角是∠BOC、∠AOD(把符合条件的角都填出来);
(2)如果∠AOC=160°,那么根据对顶角相等可得∠BOD=160度;
(3)∵OE平分∠AOD,
∴∠AOD=2∠1=64°,
∴∠2=∠AOD=64°,∠3=90°﹣64°=26°.
13.∠AOC=40 °,∠AOF=100 °,∠EOF=130°
【解析】∵OE⊥CD于点O,
∴∠EOD=90°(垂直的定义) ,
∵∠BOE=50°,
∴∠BOD=90°-50°=40°,
∴∠AOC=∠BOD=40°(对顶角相等),
∵OD平分∠BOF,
∴∠BOF=2∠BOD=80°(角平分线的定义),
∴∠AOF=180°-80°=100°,(平角的定义).
∴∠EOF=∠EOB+∠BOF=130°.
答:∠AOC=40 °,∠AOF=100 °,∠EOF=130°.
【解析】∠1=∠2,与∠1互补的角有∠3和∠4.
理由:因为∠1=∠5,∠5=∠2,
所以∠1=∠2.
因为∠1=∠5,且∠5与∠3或∠4互补,
所以与∠1互补的角有∠3和∠4.
15.【解析】
(1)∠A和∠D是由直线AE、CD被直线AD所截形成的,它们是同旁内角;
(2)∠A和∠CBA是由直线AD、BC被直线AE所截形成的,它们是同旁内角;
(3)∠C和∠CBE是由直线CD、AE被直线BC所截形成的,它们是内错角.
16.(1)如题图所示:同位角共有5对:
分别是∠1和∠5,∠2和∠3,∠3和∠7,∠4和∠6,∠4和∠9;
(2)∠4和∠5是同旁内角,∠6和∠8也是同旁内角,故∠6和∠8之间的位置关系与∠4和∠5的相同.
【解析】(1)如题图所示:同位角共有5对:
分别是∠1和∠5,∠2和∠3,∠3和∠7,∠4和∠6,∠4和∠9;
(2)由三线八角的判断方法∠4和∠5是由c,b,d三线组成,并且构成“U”形图案,所以∠4和∠5是同旁内角,同理可得:∠6和∠8也是同旁内角,故∠6和∠8之间的位置关系与∠4和∠5的相同.
故答案是:(1)同位角共有5对:分别是∠1和∠5,∠2和∠3,∠3和∠7,∠4和∠6,∠4和∠9;∠4和∠5是同旁内角;(2)∠6和∠8之间的位置关系与∠4和∠5的相同.
17.∠1与∠2是直线AB、BC被直线AC所截形成的同位角,∠3与∠4是直线AB、AC被直线BC所截形成的同位角.
【解析】∠1与∠2是直线AB、BC被直线AC所截形成的同位角,
∠3与∠4是直线AB、AC被直线BC所截形成的同位角.
18.∠1的同位角是∠B,∠2的内错角∠A;180°
【解析】由同位角的定义,内错角的定义,得
∠1的同位角是∠B,∠2的内错角∠A,
由角的和差,得∠A+∠B+∠ACB=∠ACB+∠1+∠2=180°.
19.(1)如图线段即为所求.见解析;(2)如图直线即为所求,见解析;点到直线的距离为;(3)如图直线即为所求. 见解析;(4)的同位角:.
【解析】如图线段即为所求.
如图直线即为所求,点到直线的距离为.
如图直线即为所求.
的同位角:.
试卷第1页,总3页
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
