3.2单项式的乘法课件（共32张ppt）

(共25张PPT)
下列式子哪些是单项式，哪些不是？是单项式的，它们的系数各是什么？
答：①、 ②、 ③、 ⑤、 ⑥
乘方
幂
幂的运算法则
1. am ? an＝am＋n（m、n为正整数 ）
同底数幂相乘，底数不变，指数相加.

2.（am）n＝amn （m、n为正整数）
幂的乘方，底数不变，指数相乘.

3. (ab)n＝an bn （ n为正整数）
积的乘方等于各因数乘方的积。


同学们,你们知道我们的教室有多大吗? 小明想要估算它的面积，你能帮助他解决问题吗？
小明采用步长测量教室的面积，测量长时走了13步，测量宽时走了9步，如果小明的步长用a米表示, 你能用含a的代数式表示教室的面积吗?
若小明的步长为0.7米,那么教室面积约是多少?
解:(13a) ? (9a)
(根据什么?)
(乘法交换律和结合律)
=(13 ×9 )×(a ? a)
=117a2
计算:
单项式与单项式相乘，把它们的系数、同底数幂分别相乘，其余字母连同它的指数不变，作为积的因式。
单项式乘法法则
( 2abc) ·(3ab2)
-
单项式与单项式相乘，把他们的系数、同底数幂分别相乘，其余字母连同它的指数不变，作为积的因式。
我们一起来试一试：
(1) 3ab·2a?b? (2) (–2m?n)·(6m?n?)
(3) 5xy·（-2xyz）(4) (-6ay?)·（-a?）
(5) (-3x) ?·(5xy) (6) (2x10?)(6x10?)
×
×
×
×
（1）4a2 ?2a4 = 8a8 ( )
（2）6a3 ?5a2=11a5 ( )
（3）(-7a)?(-3a3) =-21a4 ( )
（4）3a2b ?4a3=12a5 ( )
系数相乘
同底数幂的乘法，底数不变，指数相加
只在一个单项式里含有的字母，要连同它的指数写在积里，防止遗漏.
求系数的积，应注意符号
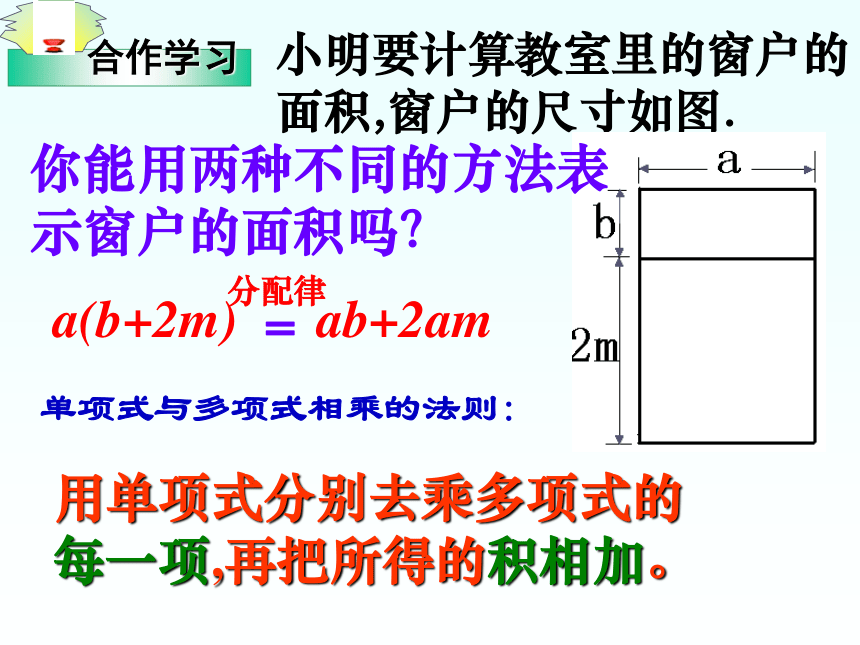
小明要计算教室里的窗户的
面积,窗户的尺寸如图.
你能用两种不同的方法表示窗户的面积吗？
a(b+2m)
ab+2am
=
分配律
用单项式分别去乘多项式的每一项,再把所得的积相加。
单项式与多项式相乘的法则:
m（a+b+c）=ma+mb+mc
单项式 ×多项式
单项式 ×单项式
法则的剖析：
1、
(x2y)(xy+1)=x3y2+1
当心符号
不要漏乘项，这样不公平
注意运算顺序，先乘（开）方，再乘除，最后算加减
+
+x2y
=4x4+4x2
2、下面的计算对不对？如果不对，应怎样改正？
第一关
第二关
第三关
第四关
基础训练：
(1) -3a·（2b）
= -6ab
(2)
细心填一填:
(1)( )
(2)
3
2
化简求值:
在一个长方形的公园修建一个草坪,如阴影所示.E是AB的中点,F是BC的三等份点.已知AB=2a,BC=3b.求草坪的面积.
我学到了什么？
单项式乘法
有理数的乘法
同底数幂相乘
积的乘方运算
转化
幂的乘方运算
单项式与多项式相乘
转化
单项式与单项式相乘

单项式乘法中要注意的几点
求系数的积，应注意符号；
相同字母因式相乘，是同底数幂的乘法，底数不变，指数相加；
只在一个单项式里含有的字母，要连同它的指数写在积里，防止遗漏；
单项式乘以单项式的结果仍然是一个单项式，结果要把系数写在字母因式的前面；
单项式乘法的法则对于三个以上的单项式相乘同样适用。
挑战自我：
1. [(-a) ?]? · [(-a?) ] ?等于 （ ）
A - a?? B a?? C a?? D - a??
(-xy?) · nx?y= 6x?y?
则 n = ____, a = ____
动脑筋：
分别计算下列图形中蓝色部分的面积
作业:
见作业本