3.3多项式的乘法(1)课件(16张ppt)
文档属性
| 名称 | 3.3多项式的乘法(1)课件(16张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 834.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-05 17:34:44 | ||
图片预览




文档简介
(共18张PPT)
课前练习
(1)(-x)3·(-x)3·(-x)5=______;
(2) (x2)4=_______;
(3) (x3y5)4=______; (4)(xy)3·(xy)4·(xy)5=______;
(5) (-3x3y)(-5x4y2z4)=_______;
(6)-3ab2(-4a+3ab-2)
=________________
-x11
x8
x12y20
x12y12
15x7y3z4
12a2b2-9a2b3+6ab2
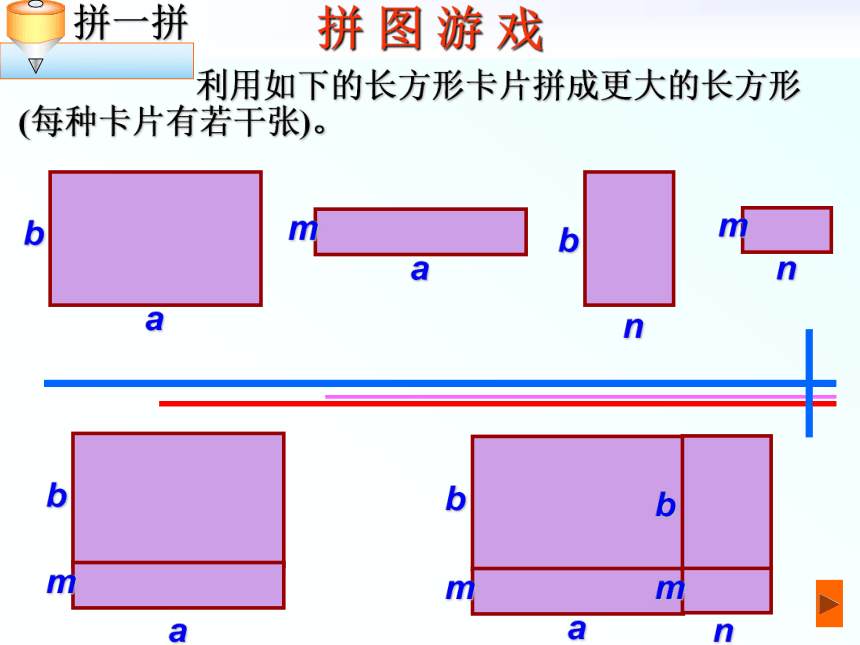
拼 图 游 戏
利用如下的长方形卡片拼成更大的长方形(每种卡片有若干张)。
a
m
n
b
n
m
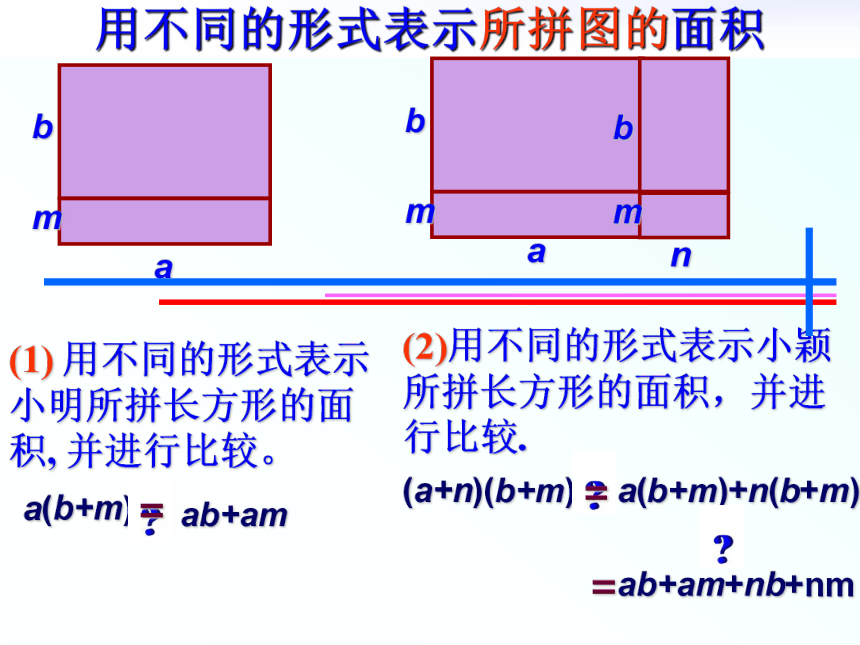
用不同的形式表示所拼图的面积
a(b+m)
(1) 用不同的形式表示小明所拼长方形的面积, 并进行比较。
(2)用不同的形式表示小颖所拼长方形的面积,并进行比较.
ab+am
=
(a+n)(b+m)
a(b+m)+n(b+m)
ab+am+nb+nm
=
=
(a+b)(m+n)
=
am
1
2
3
4
+an
+bm
+bn
多项式的乘法法则
多项式与多项式相乘, 先用一个多项式的每一项乘以另一个多项式的每一项, 再把所得的积相加.
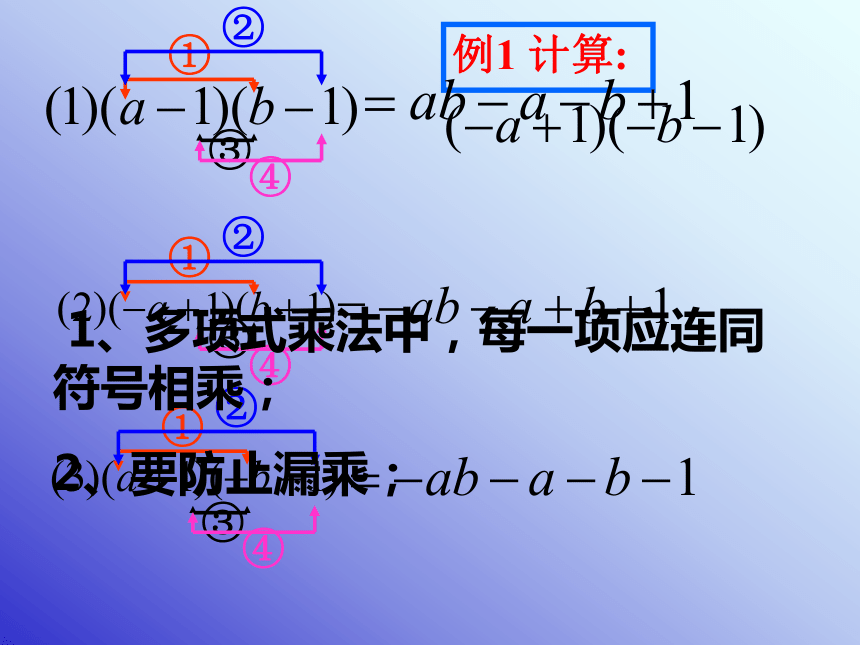
例1 计算:
1、多项式乘法中,每一项应连同符号相乘;
2、要防止漏乘;
例2 计算:
(3x-1)(x+3)
3、多项式相乘的积在没有合并同类项前,所得的项数是两 个多项式项数的积;
4、乘积中,有同类项时一定要合并,得到最简结果。
(2x – 1)(-3x) – (1 – 3x)(1 + 2x)
解:原式= – 6x2 +3x – (1 + 2x – 3x – 6x2 )
= – 6x2 + 3x – 1 + x + 6x2
= 4x – 1
例3计算
(x+1)(x2-x+1)-(x-1)2x
(2a – 3 )(3a + 1) – (6a-1)(a – 4 ), 其中
解:原式=6a2+2a-9a-3-(6a2-24a-a+4)
=6a2-7a-3-6a2+25a-4
=18a-7
运用一:先化简,再求值:
(x + 2)(x + 3) = x2 + 5x + 6;
(x + 4)(x + 2) = x2 + 6x + 8;
(x + 6)(x + 5) = x2 + 11x + 30;
根据你发现的规律,你能快速写出下面
的结果吗?
你能说出与(x + a) (x + b)相等的
多项式吗?
x2 + 8x + 15
运用二:你发现了什么?
规律:
练习:用推导的公式计算:
运用三:你会解答吗?
若(a + m) (a – 2 ) = a2 + na – 6 对 a 的任
何值都成立,求m,n值。
m = 3 , n = 1
解: (a + m) (a – 2 ) = a2 -2a+ma-2m
= a2 +(m-2)a-2m
∴n=m-2,-2m=-6
应用之四----解方程:
解:
一元二次方程
一元一次方程
2x(x-3)-(x-3)(x+8)=x2+10
1.已知A=x2+x+1,B=x+p-1,化简AB-pA.并求当x=-1时它的值.
2.计算(x3+2x2-3x-5)(2x3-3x2+x-2)时,若不展开,求出x4项的系数.
3.若(x3+mx+n)(x2-5x+3)展开后不含x3和x2项,试求m,n的值.
本节课你的收获是什么?
最后的计算结果要化简
 ̄ ̄ ̄
合并同类项.
课前练习
(1)(-x)3·(-x)3·(-x)5=______;
(2) (x2)4=_______;
(3) (x3y5)4=______; (4)(xy)3·(xy)4·(xy)5=______;
(5) (-3x3y)(-5x4y2z4)=_______;
(6)-3ab2(-4a+3ab-2)
=________________
-x11
x8
x12y20
x12y12
15x7y3z4
12a2b2-9a2b3+6ab2
拼 图 游 戏
利用如下的长方形卡片拼成更大的长方形(每种卡片有若干张)。
a
m
n
b
n
m
用不同的形式表示所拼图的面积
a(b+m)
(1) 用不同的形式表示小明所拼长方形的面积, 并进行比较。
(2)用不同的形式表示小颖所拼长方形的面积,并进行比较.
ab+am
=
(a+n)(b+m)
a(b+m)+n(b+m)
ab+am+nb+nm
=
=
(a+b)(m+n)
=
am
1
2
3
4
+an
+bm
+bn
多项式的乘法法则
多项式与多项式相乘, 先用一个多项式的每一项乘以另一个多项式的每一项, 再把所得的积相加.
例1 计算:
1、多项式乘法中,每一项应连同符号相乘;
2、要防止漏乘;
例2 计算:
(3x-1)(x+3)
3、多项式相乘的积在没有合并同类项前,所得的项数是两 个多项式项数的积;
4、乘积中,有同类项时一定要合并,得到最简结果。
(2x – 1)(-3x) – (1 – 3x)(1 + 2x)
解:原式= – 6x2 +3x – (1 + 2x – 3x – 6x2 )
= – 6x2 + 3x – 1 + x + 6x2
= 4x – 1
例3计算
(x+1)(x2-x+1)-(x-1)2x
(2a – 3 )(3a + 1) – (6a-1)(a – 4 ), 其中
解:原式=6a2+2a-9a-3-(6a2-24a-a+4)
=6a2-7a-3-6a2+25a-4
=18a-7
运用一:先化简,再求值:
(x + 2)(x + 3) = x2 + 5x + 6;
(x + 4)(x + 2) = x2 + 6x + 8;
(x + 6)(x + 5) = x2 + 11x + 30;
根据你发现的规律,你能快速写出下面
的结果吗?
你能说出与(x + a) (x + b)相等的
多项式吗?
x2 + 8x + 15
运用二:你发现了什么?
规律:
练习:用推导的公式计算:
运用三:你会解答吗?
若(a + m) (a – 2 ) = a2 + na – 6 对 a 的任
何值都成立,求m,n值。
m = 3 , n = 1
解: (a + m) (a – 2 ) = a2 -2a+ma-2m
= a2 +(m-2)a-2m
∴n=m-2,-2m=-6
应用之四----解方程:
解:
一元二次方程
一元一次方程
2x(x-3)-(x-3)(x+8)=x2+10
1.已知A=x2+x+1,B=x+p-1,化简AB-pA.并求当x=-1时它的值.
2.计算(x3+2x2-3x-5)(2x3-3x2+x-2)时,若不展开,求出x4项的系数.
3.若(x3+mx+n)(x2-5x+3)展开后不含x3和x2项,试求m,n的值.
本节课你的收获是什么?
最后的计算结果要化简
 ̄ ̄ ̄
合并同类项.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
